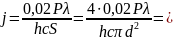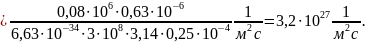Задачи к контрольным работам Тепловое излучение

Постоянная Планка. Энергетическая светимость. Испускательная способность АЧТ. Закон Стефана – Больцмана и закон Вина.

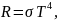
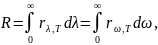
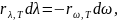
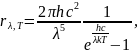
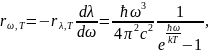
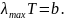
Задача. Найдите мощность ΔP, которую надо подводить к зачерненному металлическому шарику радиуса r = 2 см, чтобы поддерживать его температуру на ΔT = 27 ^oС выше, чем температура окружающей среды, равная T_ср = 20 ^oС. Считать, что тепло теряется только вследствие излучения, а излучение шарика близко к излучению ачт. Постоянная Стефана – Больцмана  = 5,6710^-8 Вт/м²·К⁴.

Решение.

При температуре шарика, равной температуре среды, он излучал бы в единицу времени световой поток мощностью, равной 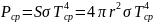. При температуре шарика T = T_ср + ΔT он будет излучать световой поток мощностью .

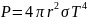Следовательно, для поддержания большей температуры шарика к нему нужно подводить мощность

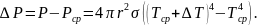
Задача. Мощность потока энергии, излучаемой из смотрового окна мартеновской печи площадью S = 6 см² равна P = 2,17 кВт. Найдите длину волны λ_max, на которую приходится максимум испускательной способности. Излучение считать близким к излучению АЧТ. Постоянная Стефана – Больцмана  = 5,6710^-8 Вт/м²·К⁴. Постоянная Вина b = 2,910^-3 мК.

Решение.

Мощность потока энергии 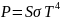. Отсюда . Длина волны максимума излучения

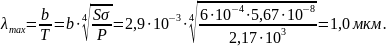
Задача. Муфельная печь потребляет мощность P = 500 Вт. Температура T ее внутренней поверхности при открытом отверстии диаметра d = 5 см равна 1000 К. Найдите, какая часть потребляемой мощности (в %) рассеивается стенками. Излучение из отверстия печи считать близким к излучению АЧТ.

Решение.

Излучаемая мощность 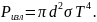Рассеивается стенками 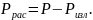Часть мощности, рассеиваемой стенками

11. Найдите приближенное среднее значение испускательной способности тела в интервале длин волн от 500 нм до 510 нм, если мощность теплового излучения 1 см² поверхности тела в этом диапазоне длин волн составляет 1 Вт.

Решение.

Обозначим мощность излучения буквой P. Среднее значение испускательной способности

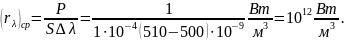
12. При нагревании АЧТ до 1500 К (T₂) длина волны, соответствующая максимальному значению испускательной способности, сместилась на 870 нм (|Δλ| = λ₁ –λ₂). Найдите, насколько процентов при этом была увеличена абсолютная температура тела.

Решение.

Используем закон Вина: 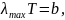откуда

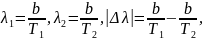
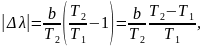
откуда

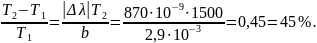
13. Найдите поглощательную способность серого тела, имеющего температуру 1000 К, если с его поверхности площадью 100 см² излучается за 100 секунд энергия 34 кДж. (Для серого тела поглощательная способность одинакова для всех длин волн излучаемого диапазона).

Решение.

Согласно закону Кирхгофа ,

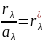поглощательная способность серого тела равна отношению энергии излучения серого тела к энергии излучения АЧТ при той же температуре:

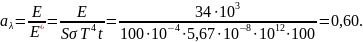
14. Используя приближенную формулу Вина r_λ = С₁^5 exp(С₂/T),найдите длину волны, соответствующую максимальному значению испускательной способности АЧТ при 2000 К. С₂ = 1,44·10^2 м·К.

Решение.

Возьмем производную от r_λ по длине волны и приравняем ее к нулю при .

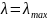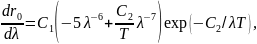
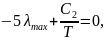
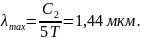
15. Шарик диаметром 1,8 см поместили в откачанный сосуд, температура стенок которого поддерживается очень низкой. Начальная температура шарика 500 К. Считая шарик абсолютно черным телом, найдите, через какое время (τ) его температура уменьшится в 2 раза. Плотность материала шарика 5,67 г/см³, удельная теплоемкость 500 Дж/кгК.

Решение.

Запишем уравнение баланса энергии: энергия, теряемая шариком за бесконечно малый промежуток времени dt вследствие излучения, равна модулю количества теплоты, теряемой шариком за это же время вследствие его охлаждения.

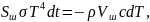
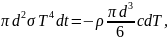
откуда

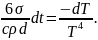
Проинтегрируем по температуре от T₀ до 0,5 T₀ и по времени от 0 до τ:

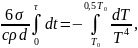
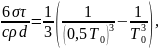
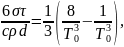
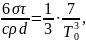
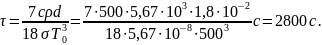
Фотоны

Энергия и импульс фотона.

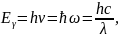
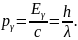
22. Излучение гелий – неонового лазера, потребляющего мощность 1 МВт, сосредоточено в пучке диаметром 0,5 см. Длина волны излучения 0,63 мкм. Найдите плотность потока фотонов (число фотонов на единицу площади в единицу времени), если на излучение идет 2 % мощности, потребляемой лазером.

Решение.

Пусть 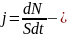плотность потока фотонов. Излучаемая мощность равна

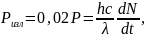
откуда