Дифференциальные уравнения. Основные понятия.

Дифференциальным уравнением называется уравнение, связывающее независимую переменную х искомую функцию у(х) и ее производные

<1>

Если функция у - есть функция одного переменного, то такое уравнение называется обыкновенным дифференциалом.

Порядок – порядок наивысшей производной, входящей в уравнение.

Решением или интегралом дифференциального уравнения называется всякая функция y=f(x), которая будучи подставлена в уравнение превращает его в тождество.

Общим решением дифференциального уравнения порядка n называется функция вида

<2>

которая удовлетворяет уравнению <1> при любом конкретном наборе постоянных C₁,C₂,C₃,…,C_n.

Задача Коши:

Дано дифференциальное уравнение <1> порядка n, найти истинное решение этого уравнения, удовлетворяющее n начальным условиям

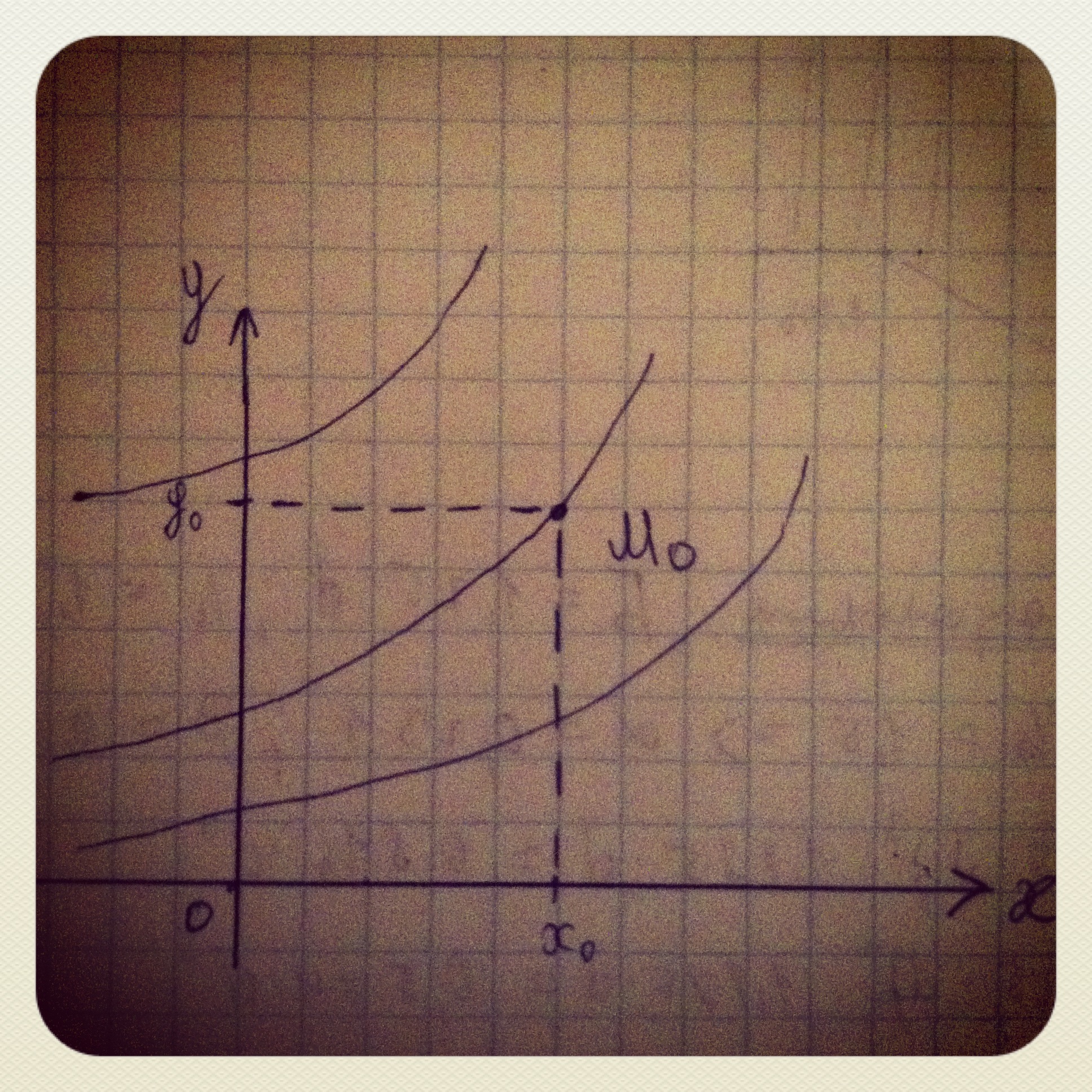
Теорема о существовании решения задачи Коши. Дифференциальные уравнения 1-ого порядка и их решения.

Теорема: Если в уравнении y’ = f(x;y) функция f(x;y) непрерывна вместе со своей частной производной y в точке М₀(x₀;y₀) и её окрестности, то уравнение имеет при (этом) том единственное частное решение, удовлетворяющее заданному начальному условию y(x₀)=y₀

Дифференциальные уравнения 1-ого порядка называются уравнения связывающие независимую переменную, искомую функцию и ее первую производную.

Дифференциальное уравнение 1-ого порядка задается в 3-х формах:

y’=f(x;y) – явная

F(x;y;y’)=0 – неявная

М(x;y)dx + V(x;y)dy=0 – дифференциальная

Решением дифференциального уравнения называется любая дифференцируемая функция y=y(x), которая при подстановке в уравнение обращает его в тождество. Интегралом уравнения называется его решение, полученное в неявном виде.

Каждое дифференциальное уравнение 1-ого порядка имеет бесконечное множество решений. Все это множество можно описать одной функцией, которая называется общим решением или общем интегралом дифференциального уравнения. Из этого множества можно выбрать конкретное (частное) решение, если задать начальное условие.

Начальным условием для уравнения 1-ого порядка является задание значение искомой функции при заданном значение независимой переменной, т.е. y(x₀)=y₀

Общим решением дифференциального уравнения 1-ого порядка называется функция y=y(x;C), которая удовлетворяет следующим условиям:

- функция содержит одну произвольную постоянную С

- эта функция является решением уравнения при любых значениях произвольной постоянной

- при заданном начальном условие произвольную постоянную можно определить единственным образом так, что полученное частное решение будет удовлетворять заданному начальному условию.

Геометрический смысл дифференциального уравнения и его общего и частного решения:

- График y=y(x) решения дифференциального уравнения y’=f(x;y) называется интегральной кривой

- Общее решение y=y(x;C) уравнение есть семейство интегральных кривых.

- Дифференциальное уравнение 1-ого порядка y’ = f(x;y) задает связь между координатами точки М(х;у) плоскости xoy с угловым коэффициентом касательной к интегральной кривой проходящей через эту точку.

- Задание начального условия y(x0) = y0 означает задание точки на плоскости М0(x0;y0).

Решить задачу Коши:

y’ = f(x;y), y(x₀)=y₀. Означает, что из всего множества интегральных кривых представляющих общее решение уравнения, необходимо отобрать ту единственную, которая проходит через данную точку М₀(х₀;у₀).

Выполнение условий теоремы Коши в точке означает, что через данную точку плоскости обязательно проходит и при том только одна интегральная кривая.

Точки (х;у) плоскости, в которых не выполняются условия теоремы Коши, называют особыми точками.

В этих (случаях) точках терпит разрыв или функция f(x;y) или ее производная f’(x;y).

Через каждую из таких точек либо проходит множество интегральных кривых, либо не проходит не одной.

Типы и решения уравнений 1-ого порядка.

1. Простейший вид:

f(x)dx + g(y)dy = 0 – уравнение с разделительными переменными.

Решение: почленyое интегрирование левой и правой его частей

⌡f(x)dx + ⌡g(y)dy = C.

2. Уравнение вида y’=f(x)g(y) – уравнение с разделяющимися переменными.

Определение: Дифференциальное уравнение y’=f(x;y) является уравнением с разделяющимися переменными, если его правая часть представляет собой, или может быть представлена в виде произведения (или отношения) двух функций, одна из которых заявляет только от х, а другая только от у т.е.

y’= f₁(x)f₂(y) или y’= f₁(x)/f₂(y) или y’ = f₂(y)/f₁(x)

Решение уравнения с разделяющимися переменными осуществляется поэтапно:

1. Пусть исходное уравнение имеет вид y’=f(x;y)

а) представляем функцию в виде произведения f(x;y) = f₁(x)f₂(y) используя алгебраические приемы:

в) Заменяем производную отношением

Уравнение примет вид

c) Умножаем обе части уравнения на dx и, одновременно, делим на функцию f₂(y), стоящую не у «своего» дифференциала. Получили:

Переменные разделены.

d) Интегрируем обе части полученного уравнения.

2. Если уравнение заданно в неявной форме, то следует из него выразить y’ в явном виде и далее действовать, как уже было сказано

3. Если уравнение задано в форме М(x;y)dx + V(x;y)dy = 0, то

а) переносим второе слагаемое в правую часть

б) каждую из двух функций представим в виде произведения (или отношения) сомножителей, например f₁(x) f₂(y)dx=g₁(x)g₂(y)dy

c)Делим обе части уравнения на произведение функций f₂(y) g₁(x), стоящих не н «своих» дифференциалов.

d) Общий интеграл находим интегрированием

.

2. Уравнение вида y’=F(ax+by+c) – уравнения, допускающие разделение переменных

Уравнение вида y’=F(ax+by+c), где а,b,c – постоянные, допускают разделение переменных, если сделать замену.

Z(x)=ax+by+c

Пример: y’= -4x+2y-6

Сделаем замену z(x)= -4x+2y-6 => y=1/2z+2x+3 => y’=1/2z’+2

Подставляем в исходное уравнение и получаем уравнение для z(x)

1/2z’+2=z => z’=2z-4 => dz/dx=2x-4

Разделяя переменные, получаем решение:

2(-4x+2y-6)-4= Ce^2x => y=1/4 Ce^2x+2x+4

2. Уравнение вида y’g(y/x) – однородное уравнение.

Определение: Дифференциальное уравнение y’=f(x;y) называется однородным, если его правая часть есть однородная функция своих аргументов f(x;y)=g(y/x)

Другими словами: уравнение первого порядка будет являться однородным, если его можно представить в виде y’=g(y/x)

Легко показать, что всякое однородное уравнение сводится к уравнению с разделяющимися переменными подстановкой y/x=t(x)

Для преобразования подстановки, необходимо:

1. Выразить в явном виде производную искомой функции из любой исходной формы записи уравнения, т.е. записать уравнение в явном виде y’=f(x;y)

2. Преобразовать функцию f(x;y) к виду f(x;y)=g(y/x) т.е. чтобы выражение, определяющее функцию содержало бы только отношение y/x и возможно константы.

3. Сделать замену y/x=t(x), y=y(x)x, y’=t’x+t которая обязательно позволит разделить переменные в полученном уравнении

2. Уравнение вида 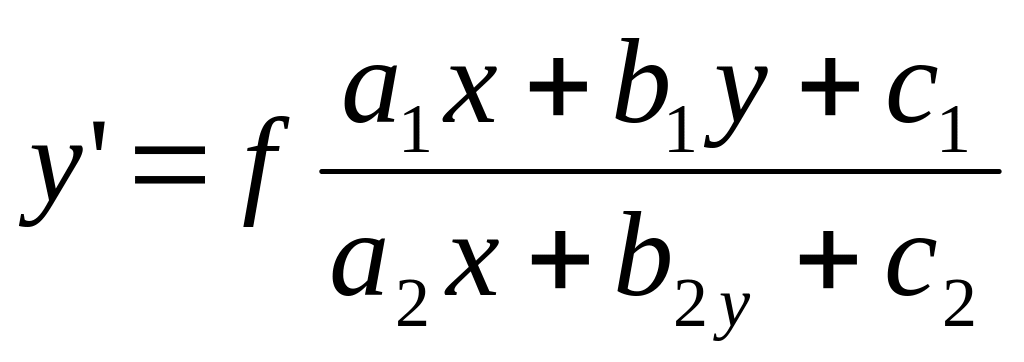– уравнения, приводящиеся к однородным.

Такие уравнения приводятся к однородному с помощью замены:

где х₀, y₀ есть решение системы

2. Уравнение вида y’+P(x)y = Q(x) – линейные уравнения.

Дифференциальное уравнение y’=f(x;y) – является линейным, если его правая часть есть линейное выражение относительно искомой функции y’=a(x)y+b(x) – Всякое уравнение 1-ого порядка будет линейным, если искомая функция и ее производная входят в уравнение в первых степенях и не перемножаются.

Решение: Метод Бернулли (Метод подстановки).

Этот метод позволяет с помощью подстановки

Y=U(x)V(x) сводить любое линейное уравнение к двум уравнениям с разделяющимися переменными относительно функции U(x) и V(x)

2. Уравнение вида 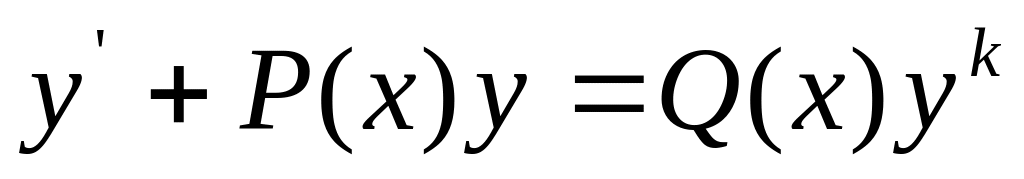- уравнение Бернулли.

Уравнением y’=f(x;y) является уравнением Бернулли, если правая часть уравнения имеет вид f(x;y)=a(x)y+b(x)y^k, к – любое рациональное число, исключается к=0 и к=1, при к=0 уравнение является линейным, а при к=1 - с разделяющимися переменными.

Замечание: Данное уравнение сводится к линейному следующим образом сначала делим на y^k

Делаем замену z(x)=y^1-k, z’(x)=(1-k)y^-ky’,

Уравнение примет вид , далее решается как линейное, например метод подстановки z=U*V

2. Уравнение вида P(x;y)dx + Q(x;y)dy=0

Уравнение P(x;y)dx + Q(x;y)dy = 0 является уравнением в полных дифференциалах, если выполняется условие

Интегрирование уравнения в полных дифференциалах производится следующим образом

1. Проверяем выполнение условия

2. Если условие выполняется, то левая часть уравнения есть полный дифференциал некоторой, пока неизвестной функции U(x;y), т.е. p(x;y)dx + Q(x;y)

dy=dU(x;y)

Тогда в соответствии с уравнением dU(x;y)=0, и поэтому общей интеграл уравнения в полных дифференциалах запишется в виде U(x;y) = C.

Таким образом, решение уравнения сводится к нахождению функции U(x;y).

Первый способ

Сравнивая выражение для полного дифференциала функции двух переменных с левой частью уравнения ,

Можем записать, что

Второй способ:

Третий способ:

Пусть требуется решить уравнение вида

P(x;y)dx+Q(x;y)dx=0

1. Проверим условие Py’=Qx’

2. Запишем систему

3. 

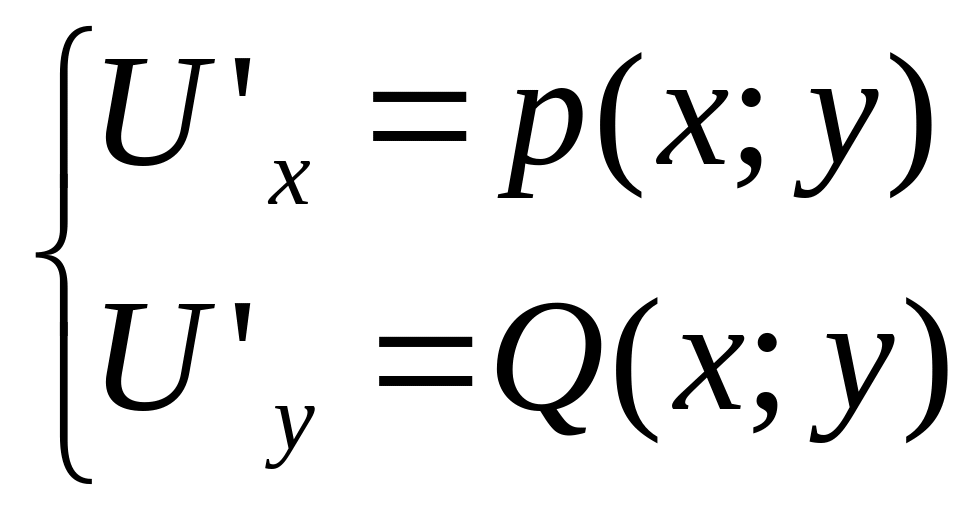
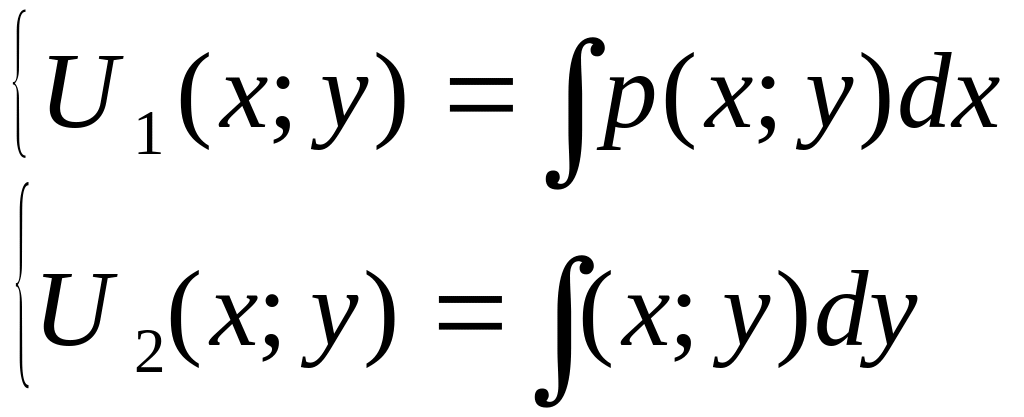
4. Записываем функцию U(x;y) = U₁(x;y)+ недостающее слагаемое из выражения для U₂(x;y)

5. Приравнивая полученную функцию константе, получим общий интеграл исходного уравнения U(x;y)=C

Метод Лагранжа (вариации произвольной постоянной).

Решение лин.урав. y’+p(x)y = Q(x) методом Лангранжа, состоит из 2-х этапов.

1. Находим общее решение однородного уравнения y’+P(x)y=0. Получим функцию y=y(x,C), С- произв. Постоянная.

2. Решение исходного уравнения ищем в том же виде, но считаем C=C(x). Подставляем функцию y=y(x,C(x)) в исходное уравнение, находим функцию C(x) и записываем общее решение исходного уравнения.

Дифференциальные уравнения высших порядков.

Дифференциальным уравнением n-ого порядка называется уравнение, которое содержит независимую переменную х, искомую функцию у, и производную n-го порядка

Уравнения n-ого порядка может быть записано в явной форме, если оно разрешено относительно старшей производной

В неявной

Решением дифференциального уравнения n-ого порядка называется любая n раз дифференцируемая функция y=y(x), которая при подстановке в уравнение, обращает его в тождество.

Начальными условиями для уравнения n-ого порядка являются задания значений искомой функции и ее производных до (n-1)-ого порядка, включительно при заданном значении х=x₀

y(x₀)=y₀ y’(x₀)= y’₀…y^(n-1)x₀=y₀^(n-1)

Задача Коши для уравнения состоит в нахождении частного решения уравнения, удовлетворяющего заданным начальным условиям.

Общим решением: уравнения называется функция , которая удовлетворяет следующим условиям:

1. Функция содержит произвольные постоянные, количество которых равно порядку уравнения.

2. Эта функция является решением уравнения при любых значения произвольных постоянных.

3. при заданных начальных условиях произвольные постоянные можно определить единственным образом так, что полученное частное решение будет удовлетворять заданным начальным условиям.

Теорема Коши: Если в уравнение функция непрерывна вместе со своими частными производными по в многомерной точке и ее окрестности, то уравнение имеет и при том единственное частное решение, удовлетворяющее заданным начальным условиям.

Дифференциальные уравнения 2-ого порядка, допускающие понижение порядка.

Тип I. Уравнение вида

Относительной особенностью такого уравнения является отсутствие в нем в явном виде самой искомой функции y и ее производных до (n-1)-ого порядка включительно.

Решением такого уравнения находится путем последовательного интегрирования.

Тип II. Уравнение вида

Относительной особенностью такого уравнения является отсутствие в нем самой функции y и ее производных до (n-2)-ого порядка включительно. Такое уравнение сводится к уравнению первого порядка подстановкой .

Тип III. Уравнения второго порядка вида

Хар-ой особенностью такого уравнения является отсутствие в нем в явном виде независимой переменной х. Порядок уравнения можно понизить до первого подстановкой: , тогда

Однородные линейные уравнения, определения, свойства решений.

Линейным дифференциальным уравнением высшего порядка называется уравнение, в котором искомая функция y(x) и ее производные входят в первых степенях и не перемножаются.

,

Где а₀,а,… - либо функции от х, либо постоянные числа.

Линейное дифференциальное уравнение 2-ого порядка имеет вид:

.

Если f(x)=0, то уравнение – однородное.

Свойства решений линейного однородного уравнения:

1. Если функция y₁(x) является каким-либо частным решением уравнения 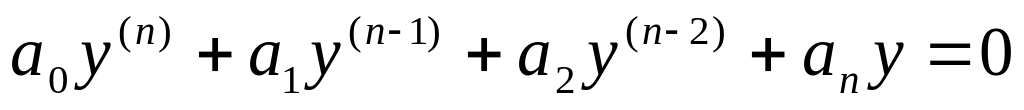, то функция ,

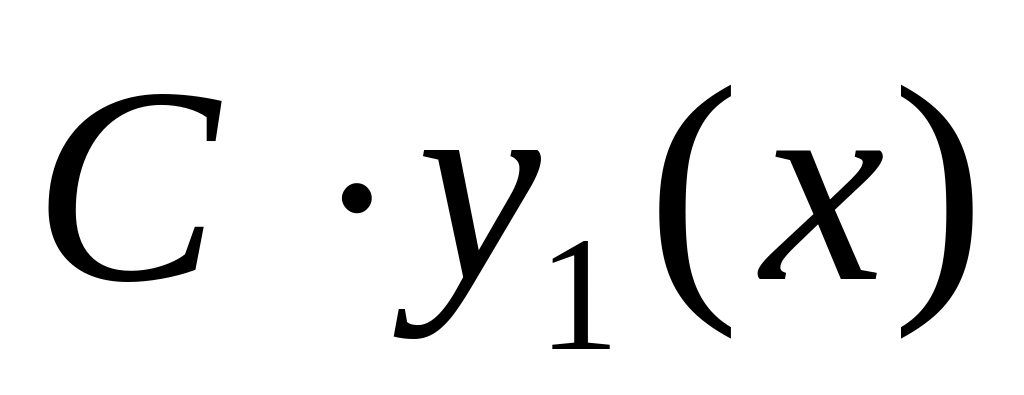где С – const, так же является решением этого уравнения.

2. Если функция 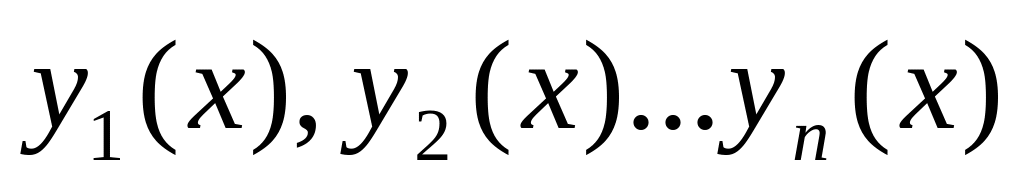- являются частными решениями уравнения , то их сумма 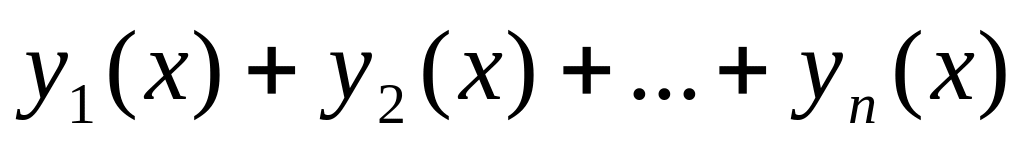также является решением этого уравнения.

3. Если функции - являются частными решениями уравнения , то их линейная комбинация 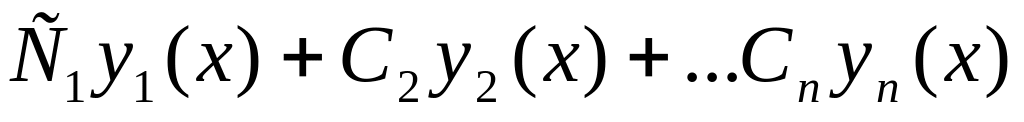также является решением этого уравнения.

Определитель Вронского (линейная зависимость и линейная независимость системы функции).

Система функций называется линейно независимой, если ни одну из этих функций нельзя представить в виде линейной комбинации остальных, например .

В частности две функции и называют линейно независимыми, если одну из них нельзя линейно выразить через другую, т.е.

или

Система функций называется линейно зависимой, если одну из этих функций можно представить в виде линейной комбинации остальных, например

В частности, две функции и называются линейно зависимыми, если существует такое число

, что или .

Общим критерием линейной зависимости и независимости системы функции является определитель Вронского.

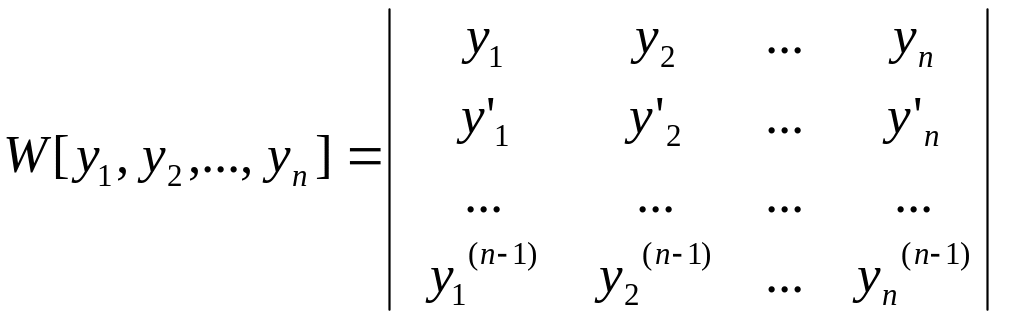
В частности, для системы двух функций определитель Вронского имеет вид:

Сформулируем критерий линейной зависимости через определитель Вронского.

Теорема 1. Если определитель Вронского , не при каких х, то система функций является линейно независимой.

Теорема 2. Если определитель Вронского тождественно равно нулю, то система функций является линейно зависимой.