Алгоритм обработки результатов многократных равноточных измерений

Если известна систематическая погрешность, то ее необходимо исключить из результатов измерений.

Вычислить математическое ожидание результатов измерений. В качестве математического ожидания обычно берется среднее арифметическое значений.

Установить величину случайной погрешности (отклонения от среднего арифметического) результата однократного измерения.

Вычислить дисперсию случайной погрешности.

Вычислить среднеквадратическое отклонение результата измерения.

Проверить предположение, что результаты измерений распределены по нормальному закону.

Найти значение доверительного интервала и доверительной погрешности.

Определить значение энтропийной погрешности и энтропийного коэффициента.

23.Обработка результатов неравноточных измерений.

Если результаты измерений получены не в одинаковых условиях и им соответствуют различные дисперсии, а следовательно, и средние квадратические погрешности, то измерения называются неравноточными. При обработке неравноточных измерений вводят новую характеристику точности измерения, называемую весом измерения. Вес результата измерения р определяется формулой: 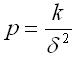 где k — произвольно выбранное число, но одно и то же для всех весов, участвующих в решении какой-либо задачи;  — дисперсия результата измерения.

Вследствие того, что точное значение дисперсии  никогда не известно, вес вычисляют по формуле т. е. принимают  , где m — средняя квадратическая погрешность, полученная по достаточно большому количеству результатов измерений. Как видно из определения веса, отношение весов не изменяется, если все веса увеличить или уменьшить в одно и то же число раз. Это является одним из свойств весов. 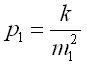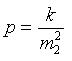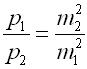Если двум результатам измерения соответствуют веса ;  то, разделив первое равенство на второе, получим т.е. веса двух измерений обратно пропорциональны квадратам средних квадратических погрешностей этих измерений. Равенство выражает второе свойство весов. Из определения веса следует, что неравноточные измерения имеют неравные веса.

24.Обработка результатов совместных и совокупных измерений.

Совместное измерение — одновременное измерение нескольких неодноименных величин для нахождения зависимости между ними. При этом решается система уравнений.

Совокупное измерение — это проведение ряда измерений (чаще всего прямых, но, вообще-то, измерения из ряда могут быть любыми — вспомните, как получаются сложные функции в математике) нескольких величин одинаковой размерности в различных сочетаниях, после чего искомые значения величин находятся решением системы уравнений. Число уравнений при этом должно быть равно числу измерений.

Эти виды измерений характеризуются тем, что значения искомых величин рассчитывают по системе уравнений, связывающих их с некоторыми другими величинами, определяемыми посредством прямых или косвенных измерений. При этом измеряются несколько комбинаций значений указанных величин. Каждая такая комбинация позволяет получить одно уравнение, а система содержит всю информацию о значениях искомых величин и имеет вид

где F; — символ функциональной зависимости между величинами в i-м опыте; i=1; 2;...; n; n — число опытов; Q_j — значения искомых величин, общее число которых равно m; Х_г⁽ⁱ⁾ — полученные в i-м опыте значения k величин, измеряемых прямыми или косвенными методами.

Если Q_i являются значениями одной и той же величины, то измерения называются совокупными, если разных физических величин, — то совместными.

Для того чтобы рассчитать значения искомых величин, достаточно иметь m уравнений, т.е. столько же, сколько содержится неизвестных. Тогда результаты измерений и доверительные границы их погрешностей можно найти методами обработки результатов косвенных измерений. Однако обыкновенно для уменьшения погрешностей результатов измерений делается значительно больше измерений, чем это необходимо для определения неизвестных, т.е. n > m.