20. Интервальные оценки числовых характеристик. Понятия доверительной вероятности, доверительного интервала и доверительных границ.

Интервал значений случайной величины, внутри которого с заданной вероятностью находится истинное значение погрешности результата измерения, называется доверительным интервалом погрешности результата измерения, а соответствующую ему вероятность — доверительной вероятностью 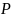. Нижнюю и верхнюю границы доверительного интервала называют доверительными границами. Доверительный интервал характеризует степень воспроизводимости результатов измерения. Как следует из определения, для характеристики случайной погрешности необходимо иметь две характеризующие ее величины — доверительный интервал и доверительную вероятность.

21.Обработка результатов измерений с однократными наблюдениями.

Измерения с однократными наблюдениями. За результат измерения в этом случае принимают результат однократного наблюдения х, используя предварительно полученные данные об источниках, составляющих погрешность. Доверительные границы  (неисключённой систематической погрешности) (НСП) результата измерения Θ(Р) вычисляют по формуле:

где k(P) — коэффициент, определяемый принятой Р и числом m₁ составляющих НСП: Θ(Р) — найденные нестатистическими методами границы j-й составляющей НСП. Среднее квадратическое отклонение (СКО) результата измерения с однократным наблюдением вычисляют одним из следующих способов: Если в технической документации на СИ или в МВИ указаны нормально распределенные составляющие случайной погрешности результата наблюдения (инструментальная, методическая, из-за влияющих факторов, оператора и т. д.), то СКО вычисляют по формуле

г	m2 — число составляющих случайной погрешности; Si — значения СКО этих составляющих.

Доверительную границу случайной погрешности результата измерения е (Р) в этом случае вычисляют по формуле

где Ζ_P/2 — значение нормированной функции Лапласа в точке Р/2 при доверительной вероятности Р.Если в тех же документах случайные составляющие погрешности результата наблюдения представлены доверительными границами ∈_i, (Р) при одной и той же доверительной вероятности Р, то доверительную границу случайной погрешности результата измерения с однократным наблюдением при доверительной вероятности вычисляют по формуле

Если случайные составляющие погрешности результата наблюдения определяют предварительно в реальных рабочих условиях экспериментальными методами при числе наблюдений n_i < 30, то:

где	t — коэффициент Стьюдента, соответствующий наименьшему числу наблюдений nm из всех ni можно найти в  или в любом справочнике по теории вероятностей;  S(x) — оценки СКО случайных составляющих погрешности результата наблюдения.

22.Обработка результатов прямых многократных равноточных измерений.

Прямые измерения – это измерения, посредством которых непосредственно получается значение измеряемой величины.

Равноточными или равнорассеянными называют прямые, взаимно независимые измерения определенной величины, причем результаты этих измерений могут быть рассмотрены как случайные и распределенные по одному закону распределения.

Обычно при обработке результатов прямых равноточных измерений предполагается, что результаты и погрешности измерений распределены по нормальному закону распределения.

После снятия расчетов вычисляется значение математического ожидания по формуле:

где x_i – значение измеряемой величины;

n – количество проведенных измерений.

Затем, если систематическая погрешность определена, ее значение вычитают из вычисленного значения математического ожидания.

Потом вычисляется значение среднеквадратиче-ского отклонения значений измеряемой величины от математического ожидания.