Поверхности

Кинематическое образование поверхности

Классификация поверхностей

Способы задания поверхностей:

1)Аналитический

2)Кинематический

3)Каркасный

Под кинематическим образованием поверхностей понимают непрерывное перемещение в пространстве по определённому закону линии или поверхности. Такие линии или поверхности называются образующей поверхностью. Если известны законы, по которым непрерывно перемещается образующая поверхность, называется закономерной, в противном случае называется незакономерной.

-

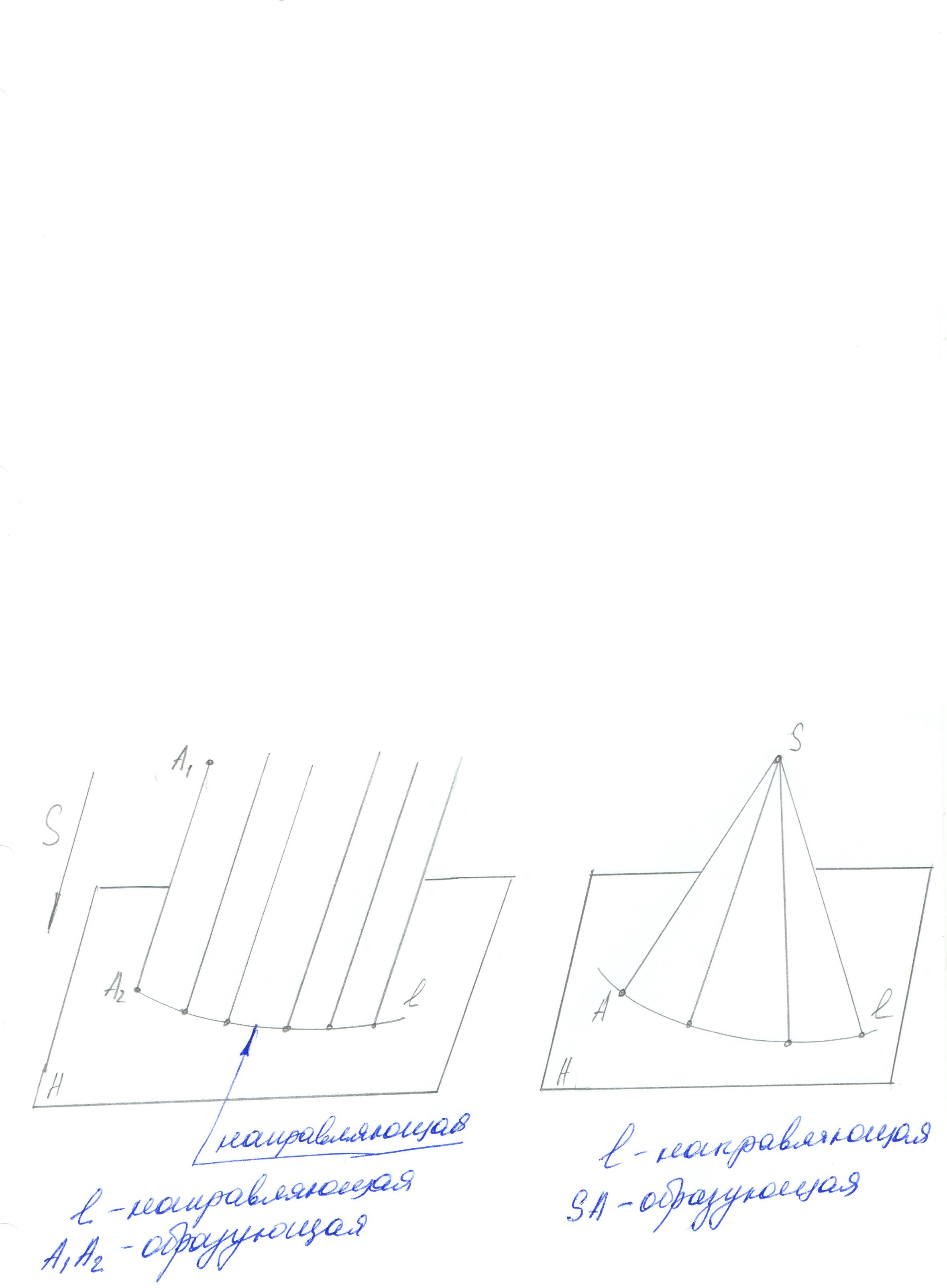
Поверхности полученные перемещением прямой линии по какому-либо закону называются линейчатыми.

Одна и таже поверхность может бать получена разными способами.

Например коническую и цилиндрическую поверхности можно получить и способом вращения (если направляющей является окружность) .

П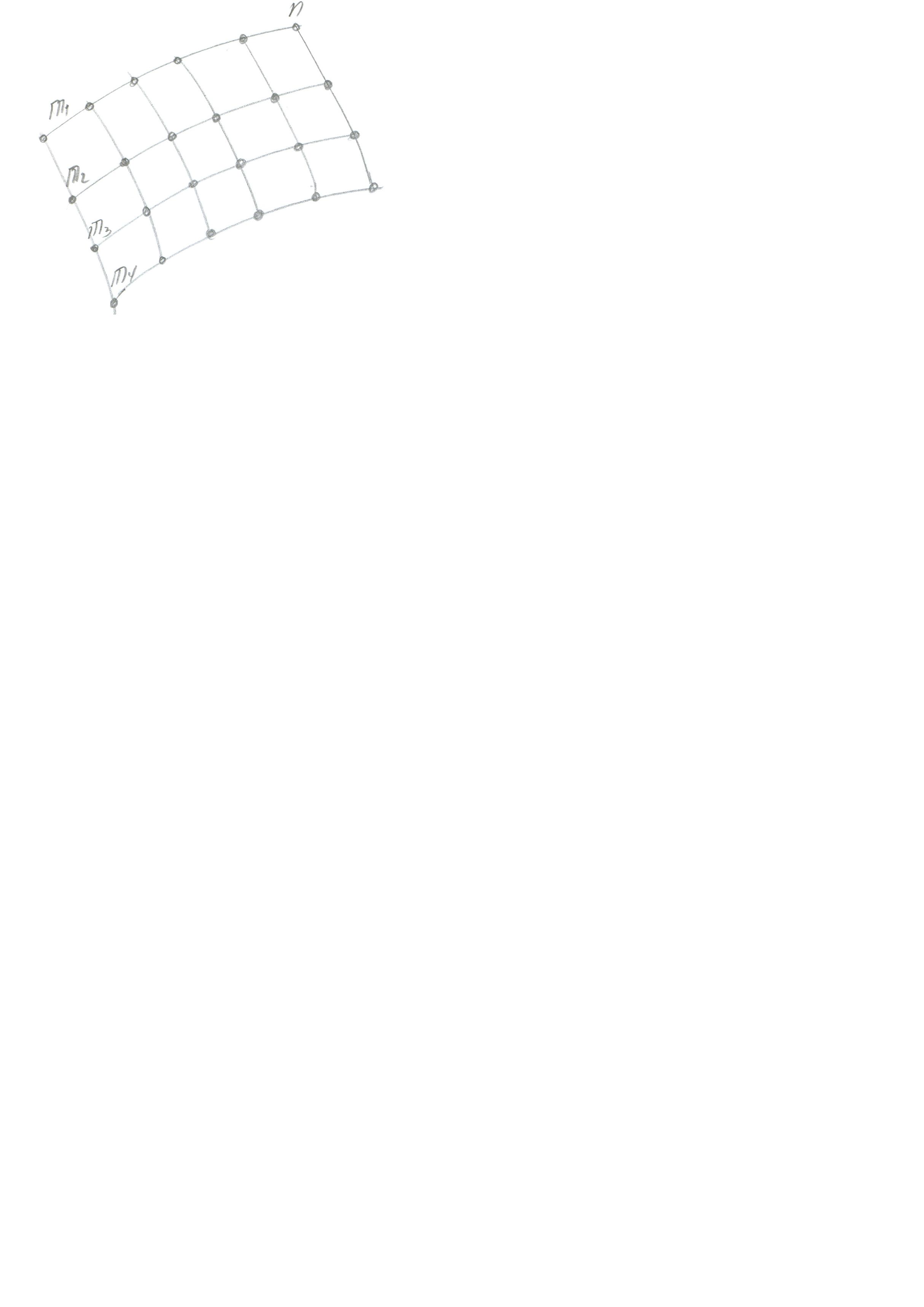 оверхность можно задать и каркасом,

Пусть мы имеем каркас или сетку, жёстко связанную в точках пересечения.

Каркасом задаются обычно сложные поверхности не подчиняющиеся никаким законам. Примером каркасных поверхностей служат поверхности: корпуса судов, самолётов, автомобилей.

Классификация поверхностей

1. Поверхности вращения, образуемые вращением произвольной образующей вокруг неподвижной оси(пов-ти 2-го порядка )

2. Линейчатые поверхности образуемые движением прямых.

3. Винтовые поверхности, образуемые винтовыми движениями прямых

4. Каркасовые поверхности.

-

Задать поверхности на чертеже, значит указать условия, позволяющие построить каждую точку поверхности Если хотят придать изображению большую наглядность, то вычёркивают ещё и очерк поверхности.

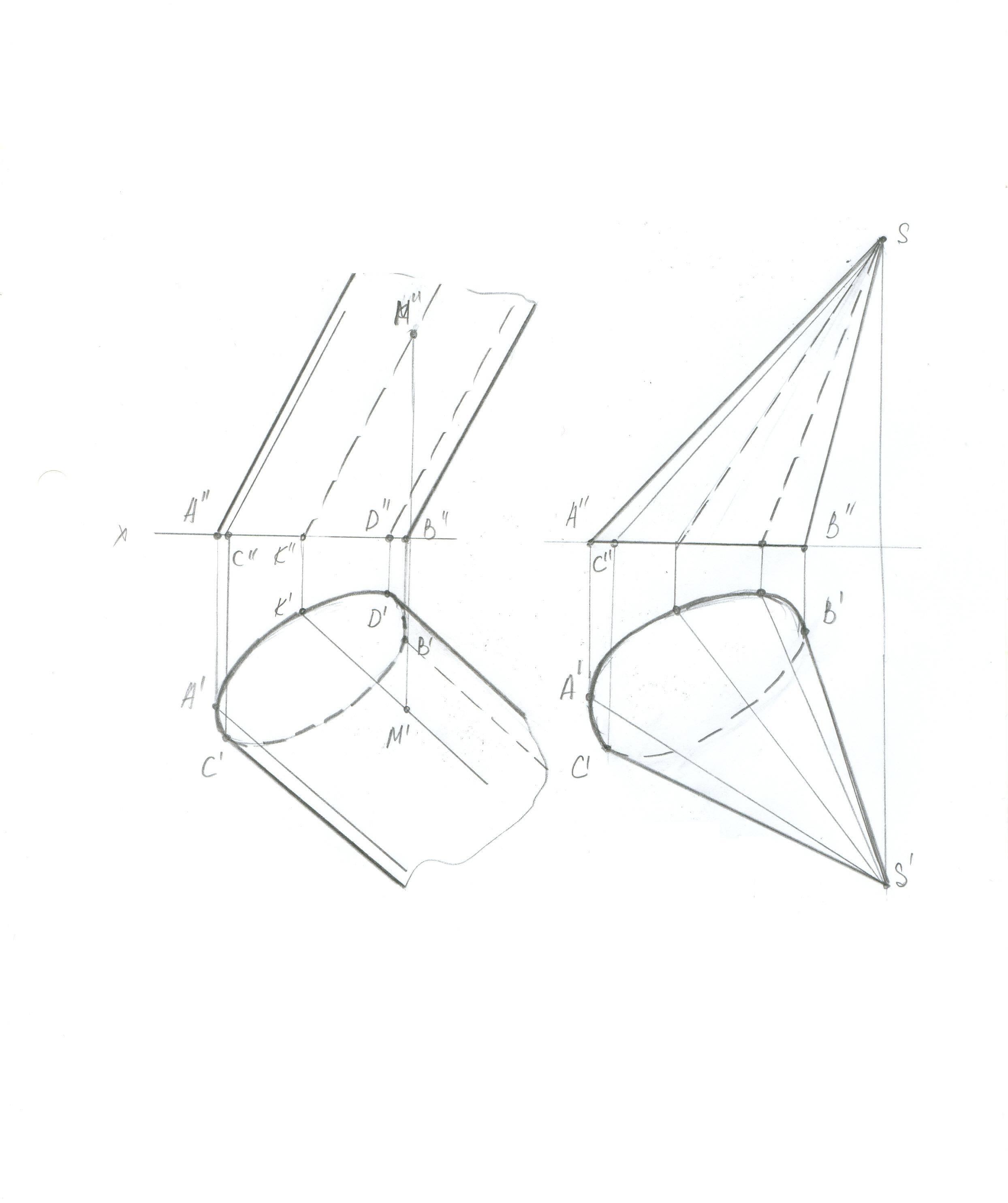
Чтобы построить точку на поверхности нужно построить линию, принадлежащую поверхности.

Если в качестве направляющей будет ломаная линия (многоугольник), то образуется призматическая и пирамидальная поверхность.

Рассмотрим поверхности вращения

-

Поверхности вращения

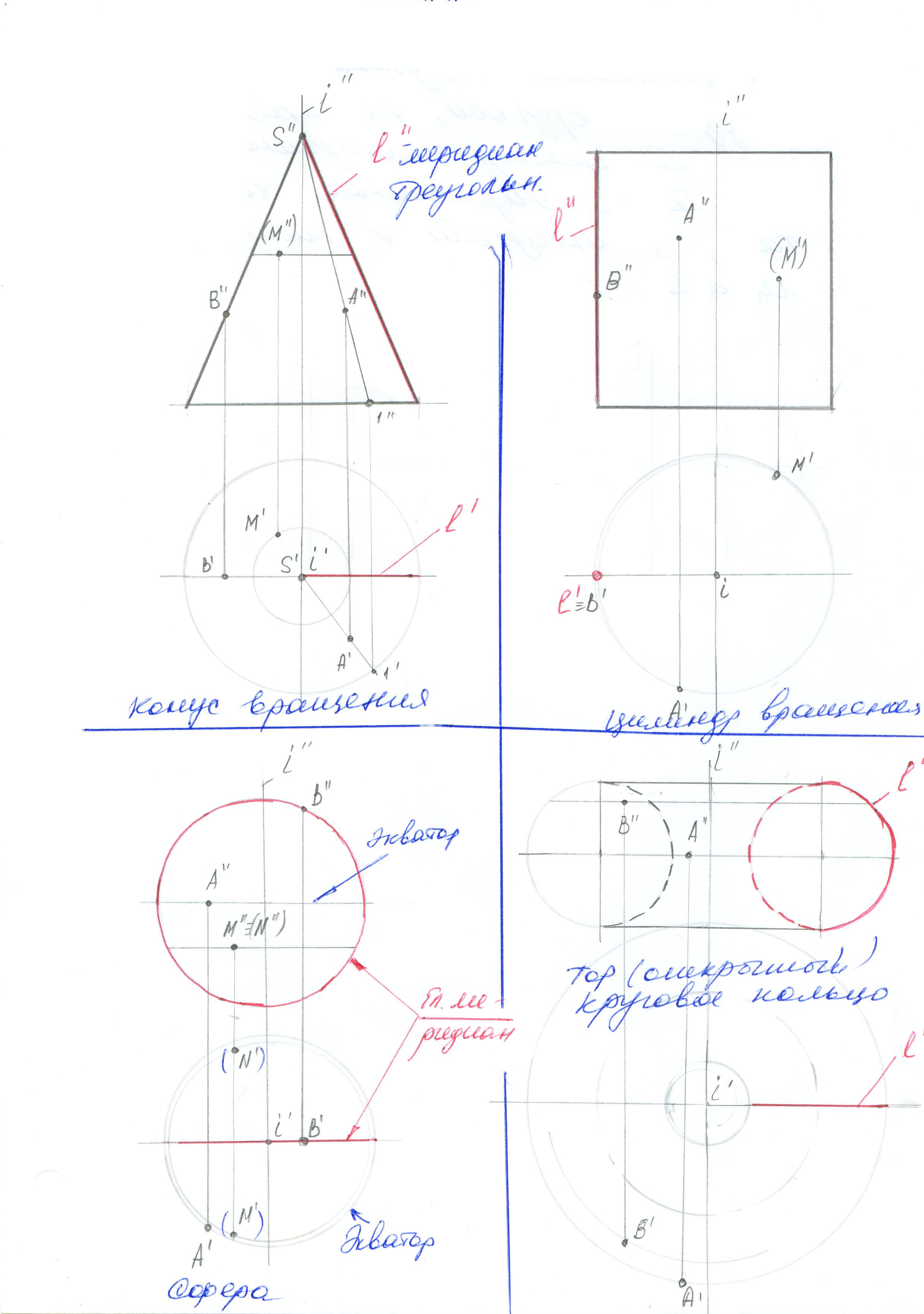
Поверхностью вращения называют поверхность получаемую от вращения какой либо линии (образующей) вокруг неподвижной оси.

Образующая зафиксирована в том или ином положении называется меридианом.

Если пересекать поверхности вращения плоскостями перпендикулярными к оси вращения, получаются в сечении окружности. Такие окружности называются параллелями .Наибольшую из параллелей называют экватором, наименьшую горлом.

Конические сечения

Пересечение поверхностей

I Пересечение поверхностей, если одна из них является проецирующей.

Прежде чем приступить а построению линии пересечения поверхностей, необходимо внимательно изучить условие задачи, т.е. какие поверхности пересекаются.

Если одна из поверхностей является проецирующей, то решение задачи упрощается, т.к. на одной из проекций линия пересечения совпадает с проекцией поверхности. И задача сводится к нахождению второй проецирующей линии.

При решении задачи следует отметить в первую очередь «характерные» точки или «особые».

Это :

• Точки на крайних образующих

• Точки, делящие линию на видимую и невидимую часть

• Верхние и нижние точки и др.

Далее следует разумно выбрать способ, каким будем пользоваться при построении линии пересечения поверхностей.

Мы будем пользоваться двумя способами:

1. вспомогательных секущих плоскостей.

2. вспомогательных секущих сфер.

Прмеры:

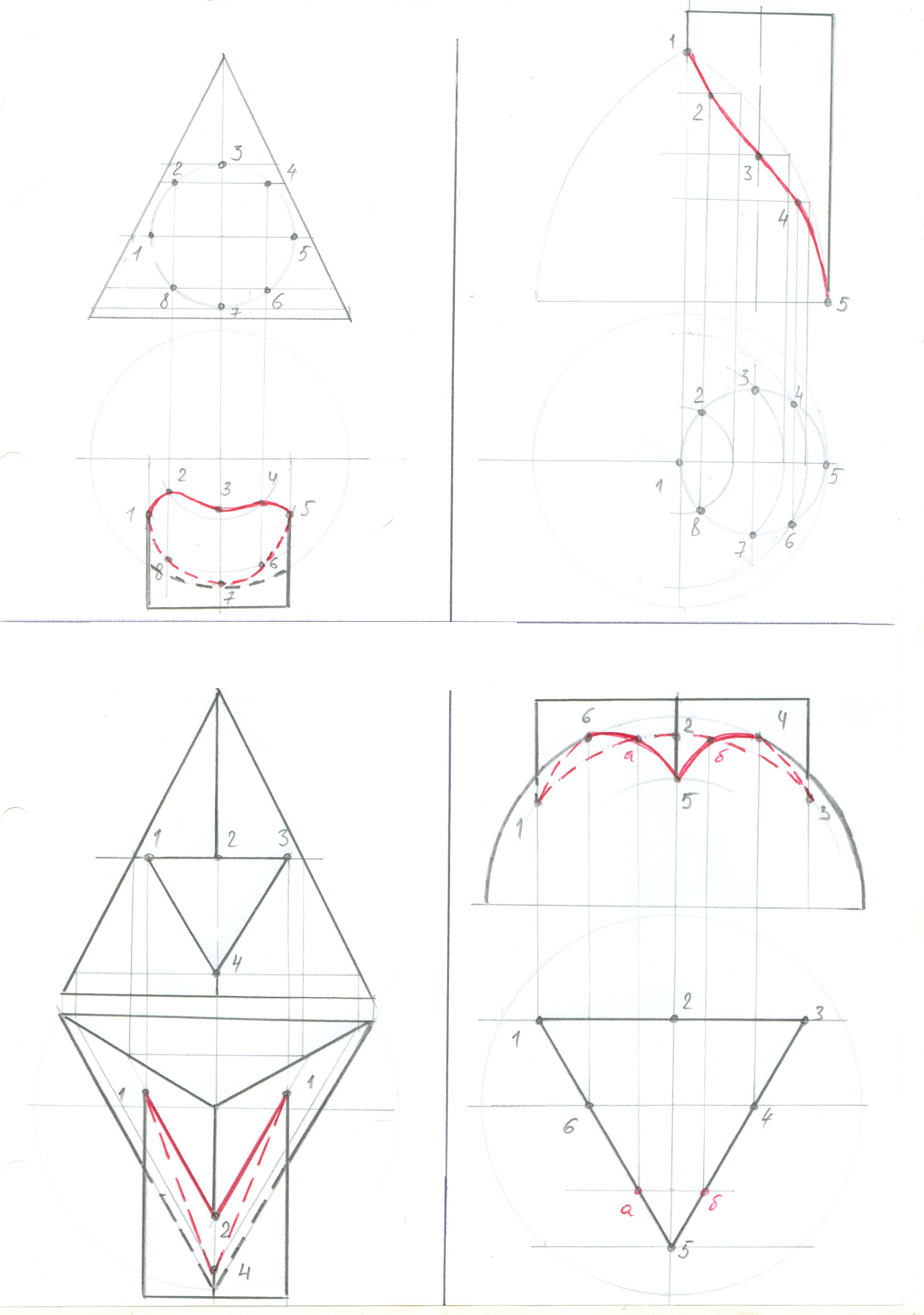
Построение линий пресечения способом вспомогательных секущих плоскостей

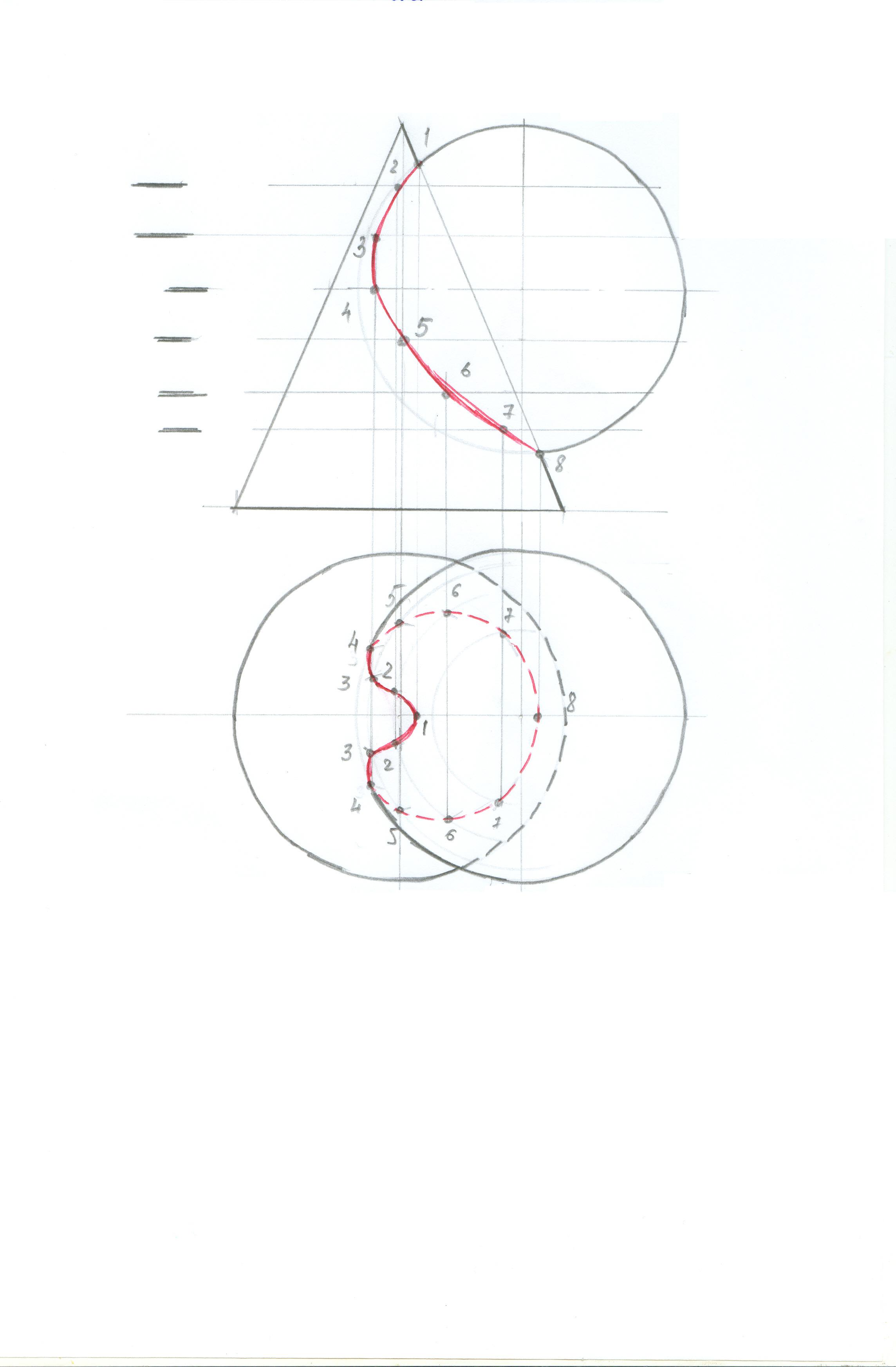
В данном случае в качестве плоскостей-посредников мы выбираем горизонтальные секущие плоскости, которые пересекают конус и сферу по окружностям. Если секущая плоскость-посредник пересекает хотя бы одну поверхность по линиям сложным в построении, такие плоскости в качестве вспомогательных применять нельзя.