33

Начертательная геометрия. Инженерная графика

Лекций - 18 часов Практических – 54 часа Экзамен – I семестр

Литература:

Гордон В.О.,Семенцов – Оглевский М.А. «Курс начертательной геометрии»/Под редакцией Ю.Б. Иванова, издательство «Наука», 1988г.

Задачи:

1. Научить строить чертежи, т.е. изображать пространственные трехмерные образы на плоском двухмерном чертеже (Прямая задача)

2. Научить читать чертежи, т.е. по плоскому изображению представить технический объект предметного пространства (обратная задача)

3. Научить на плоском чертеже решать позиционные и метрические задачи относительно взаимного положения пространственных объектов.

В число дисциплин, составляющих основу инженерного образования, входит начертательная геометрия.

Предметом начертательной геометрии является изложение и обоснование способов изображения пространственного образов (линий, поверхностей, тел) на плоскости и способов решения геометрических задач по заданному изображения этих тел.

Построение изображений основанных на методе проекций.

Изучение метода проекций начинается с построения точки, т.к. любой пространственный объект рассматривают как ряд точек, принадлежащих этому объекту.

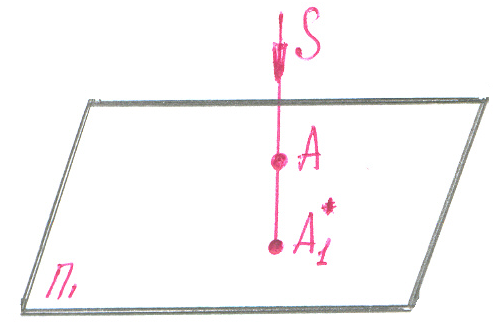
Проекцией т. А на плоскость П1 называется т. А1 *, полученная при пересечении проходящего через нее проецирующего луча с площадью проекций П1- площадь проекций А - объект проецирования SA – проецирующий луч А1 – проекция точки А

В зависимости от способа проведения проецирующего луча проекции подразделяют на центральные и параллельные.

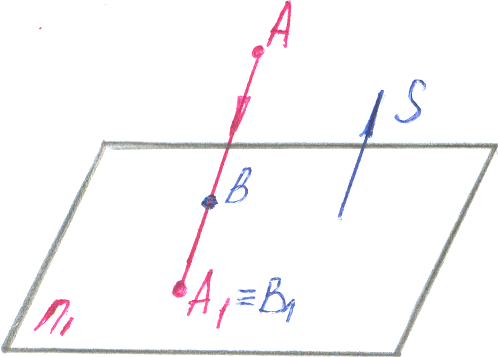
Параллельные проекции, получающиеся в случае расположения проецирующих лучей // между собой и // заданному направлению проецирования

В свою очередь параллельные проекции могут быть прямоугольные (ортогональные) и косоугольные

А1, А2 – проекции т. А на плоскость П1. Как видно из чертежа, одна проекция точки не определяет положение её в пространстве, т. к. может служить проекцией в любой точке, лежащей на проецирующем луче. Для получения полного изображения применяющей проекции на 2 и 3, иногда и более плоскости проекции.

Прямоугольное проецирование. Проекции точки на 2 и 3 плоскости проекций.

H - Горизонтальная плоскость проекции

V – Фронтальная плоскость проекции

W - Профильная плоскость проекции

0X 0Y 0Z – оси проекций

A' - Горизонтальная проекция

A''- Фронтальная проекция A'''- Профильная проекция

А'А и А''А Горизонтальная и фронтальная проецирующие прямые

Из чертежа видно, что две проекции точки определяют положение её в пространстве. Третья проекция используется в отдельных случаях.

Координаты точки А X,Y,Z(они определяют расстояние до плоскостиW,H,V) A' A''- вертикальная линия проекционной связи A'' A''' – горизонтальная линия проекционной связи A'Aу и A'''Ау – горизонтальная и вертикальная линии проекционной связи

Эпюр Монжа

Предложен Гаспаром Монжа в 1799г. В труде «Начертательная геометрия»

Основной закон проецирования:

Две проекции точки всегда лежат на одной линии связи параллельно одной из осей проекции.

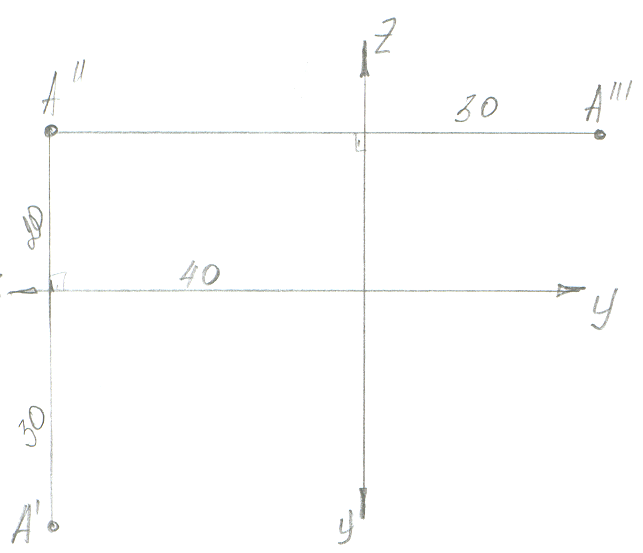
Пример: Построить три проекции точки А по заданным координатам

А(40,30, 20)

Классификация точек:

1. Точки лежат в пространстве

   • Ни одна из трех координат на равно нулю

   • Ни одна из проекций не совпадает с самой точкой.

2. Точки лежат на одной из плоскостей проекции

• Одна из трех координат равна нулю

• Одна проекция совпадает с самой точкой.

3. Точки лежат на одной из осей

• Две координаты точки равны нулю.

• Две проекции точки совпадают с самой точкой.

Лекция 2

I - Задание прямой.

II - Классификация прямых:

1. общего положения

2. уровня

3. проецирующие

III – Взаимное положение прямых.

I Проекции прямой. Принадлежность точки прямой.

Проекция прямой линии есть прямая. Прямая может быть определена: двумя точками точкой и направлением если точка принадлежит прямой, то проекция точки принадлежат одноименным проекциям прямой.

II Классификация прямой:

1. Прямая общего положения – это прямая не параллельная и не перпендикулярная ни одной из плоскостей проекций

   • На эпюре проекции такой прямой не параллельная и не перпендикулярна оси 0Х.

   • Проекция такой прямой всегда меньше самой прямой

2. Прямая параллельная одной из плоскостей проекции (прямая уровня)

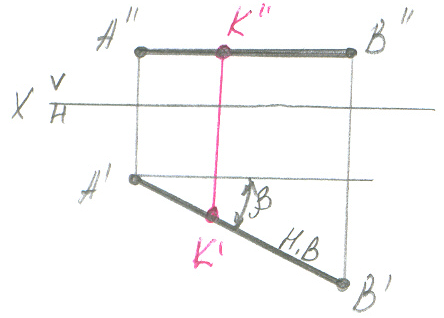
АВ || Н- горизонтальная прямая	СD || V – фронтальная прямая

MN || W – профильная прямая α и β – углы наклона прямой к плоскостям H и V

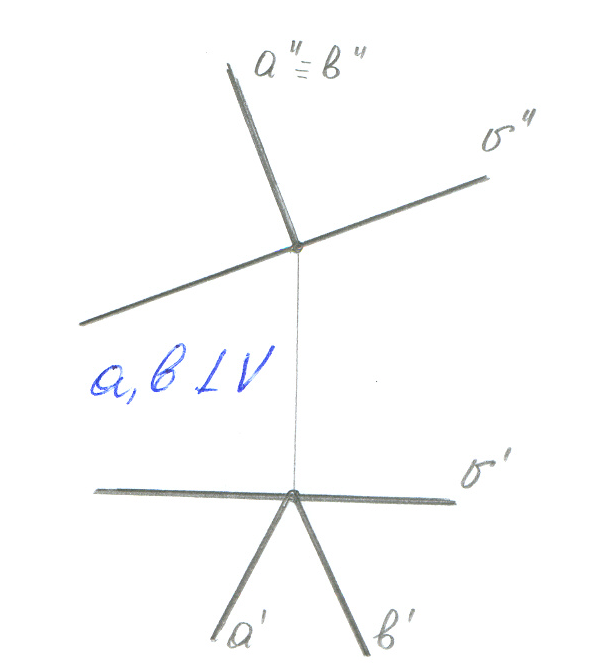
3. Прямая параллельна двум плоскостям проекциям или перпендикулярна одной из плоскостей (проецирующая прямая)

m- горизонтально проецирующая	n- фронтально проецирующая	k- профильно проецирующая

III – Взаимное положение двух прямых.

1. Пересекающиеся прямые

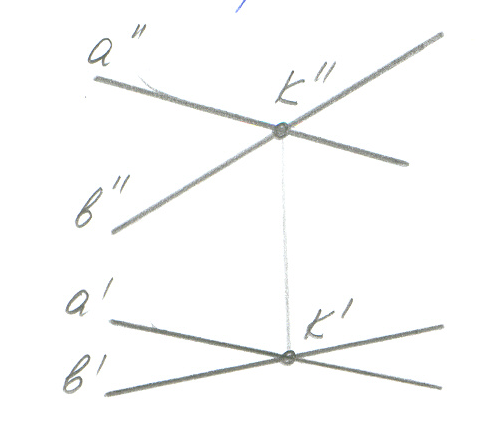
Если а и b пересекаются, то их одноименные проекции пересекаются и точка пересечения лежит на одной линии связи a'∩b'→k' a∩b = k a''∩b''→k'' a'''∩b'''→k'''

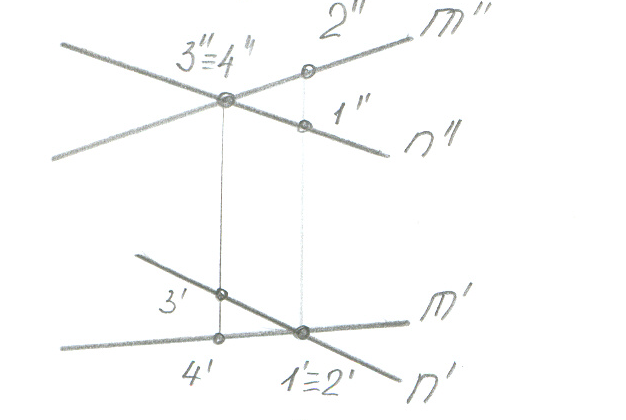
2. Скрещивающиеся прямые

Прямые которые не параллельны и не пересекаются

3. Параллельные прямые.

Если прямые в пространстве параллельны, то их одноименные проекции тоже параллельны C' || D' C||D→ C'' || D'' C''' || D'''	Чтобы убедиться параллельны ли прямые, следует построить профильные проекции этих прямых.

Определение Н.В. отрезка прямой и углов его наклона к плоскости или проекции методом прямоугольного треугольника.

Угол наклона прямой с плоскостью – есть угол между прямой и ее проекцией на данную плоскость.

Для определения Н.В. отрезка нужно построить прямоугольный треугольник, у которого один конец есть проекция на плоскость, а другой - разность расстояний концов отрезка до этой плоскости.

Проекция плоских углов.

Теорема: Если обе стороны любого угла параллельны плоскости проекции,

его на эту плоскость он проецируется в Н.В.(без искажения)

если одна сторона прямого угла параллельна плоскости проекций. А другая сторона ей не перпендикулярна, то прямой угол проецируется на эту плоскость без искажений.

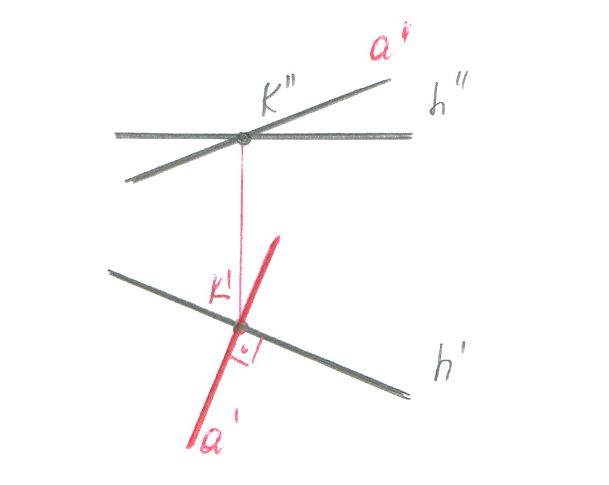
Если горизонталь и любая другая прямая перпендикулярны, то на чертеже их горизонтальные проекции перпендикулярны Пример 1: Из точки А. опустить перпендикуляр на прямую υ	Если фронталь и любая другая прямая перпендикулярны, то на чертеже их фронтальные проекции перпендикулярны. Пример 2: Построить горизонтальную проекцию прямой a┴h
Пример 3: Определить расстояние от точки А до прямой h

Плоскость. Задание плоскость на чертеже. Принадлежность точки и прямой плоскости.

I Положение плоскости в пространстве определяется:

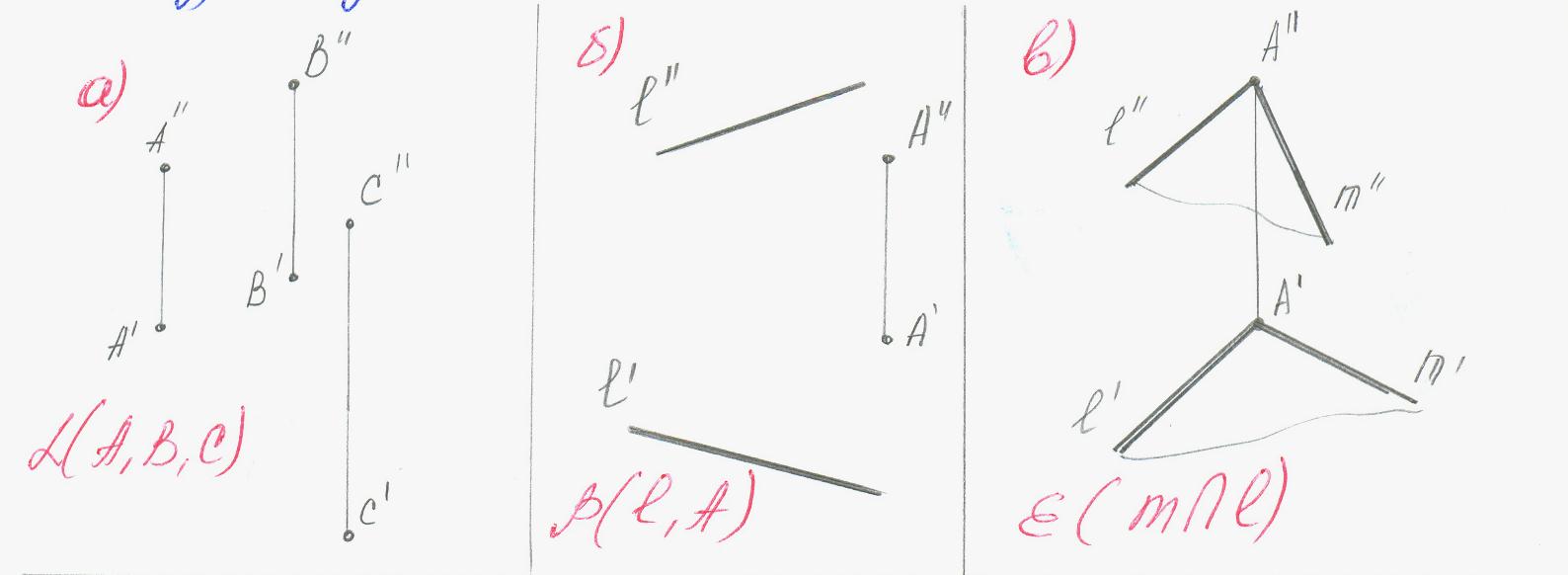
1. Тремя точками не лежащими на одной прямой.

2. Прямой и точкой, вне этой прямой

3. Двумя пересекающимися прямыми

4. Двумя параллельными прямыми

5. Следами плоскости.

αh- горизонтальный след плоскости

αv- фронтальный след плоскости

αx- точка схода следов

След плоскости- это прямая, по которой плоскость пересекается с плоскостью проекций.