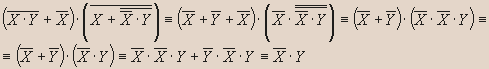- •Урок №1-2 тема "алгебра высказываний. Основные операции алгебры высказываний"
- •I. Беседа с учащимися (файл matlog1.Ppt)
- •3. Прочтите формулы:
- •Ход урока.
- •20 Вопросов
- •Новый материал.
- •1. Установление истинности сложных высказываний.
- •2. Эквивалентность высказываний.
- •3. Тавтология.
- •I. Актуализация опорных знаний.
- •II. Составление таблиц истинности.
- •Самостоятельная работа. Вариант №1.
- •Вариант №2.
- •Домашнее задание.
- •Законы де моргана. Тождественность высказываний. Упрощение формул. План урока.
- •Ход урока.
- •I. Подача нового материала.
- •1. Упрощение формул.
- •2. Преобразования “поглощение” и “склеивание”
- •3. Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям.
- •4. Любую формулу можно тождественно преобразовать так, что в ней не будут использованы:
- •5. Замена эквиваленции и импликации на конъюнкцию, дизъюнкцию и отрицание.
- •II. Практическая работа на эвм.
- •I. Проверка домашнего задания (файл д_з3.Doc).
- •II. Решение логических задач.
- •2. Графический способ решения систем логических уравнений.
- •3. Решение логических задач на эвм.
- •Решение контрольной работы №1 "Истинность высказываний. Тавтологии. Эквивалентности. Законы логики. Тождественные преобразования". Вариант №1.
- •Вариант №2.
- •Вариант №3.
- •Вариант №4.
- •Решение логических задач.
- •План урока.
- •Ход урока.
- •I. Проверка домашнего задания.
- •II. Решение задач.
- •Задача.
- •I. Актуализация опорных знаний. Беседа.
- •II. Логические основы построения эвм.
- •III. Структурные формулы и функциональные схемы.
- •IV. Построение логического выражения по таблице истинности
- •V. Домашнее задание.
- •Применяя законы и правила преобразования формул булевой алгебры упростить выражения:
- •Решение.
- •Построить логические схемы, реализующие заданные функции:
Вариант №4.
Докажите эквивалентность:
 Решение.
Решение.
A
B



0
0
0
1
1
0
0
1
1
0
0
0
1
0
1
1
1
1
1
1
1
0
1
1
Вывод. Из таблицы видно, что

Докажите, является ли данное высказывание тавтологией: Решение
X
Y

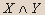


0
0
1
0
0
1
1
1
0
1
1
0
0
1
1
1
1
0
0
1
0
0
0
0
1
1
1
0
1
0
1
1
Вывод. Из таблицы видно, что высказывание не является тавтологией.
Установите истинность высказывания: Решение.
C
D
E
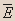


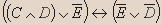
0
0
0
0
1
1
1
1
1
0
0
1
0
0
0
1
1
0
0
1
0
0
1
1
0
1
1
0
1
1
0
0
0
0
0
1
1
0
0
0
1
1
1
1
1
1
0
1
0
0
0
1
1
0
1
1
0
1
1
1
0
1
1
1
1
1
1
0
1
0
0
0
Вывод. Из таблицы видно, что высказывание истинно всегда, кроме случая: 1. C 0; D 0; E 1; 2. C 1; D 0; E 1; 3. C 1; D 1; E 1;
Для формулы придумайте формализуемое ею высказывание:
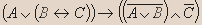 Решение.
Пусть:
A— «Коля пишет письмо»
B—
“Дима смотрит телевизор”
C—“Игорь
разговаривает по телефону”
Если
Коля пишет письмо или тогда и только
тогда Дима смотрит телевизор, когда
Игорь разговаривает по телефону, то
неверно что, Коля пишет письмо или Дима
смотрит телевизор и Игорь не разговаривает
по телефону.
Решение.
Пусть:
A— «Коля пишет письмо»
B—
“Дима смотрит телевизор”
C—“Игорь
разговаривает по телефону”
Если
Коля пишет письмо или тогда и только
тогда Дима смотрит телевизор, когда
Игорь разговаривает по телефону, то
неверно что, Коля пишет письмо или Дима
смотрит телевизор и Игорь не разговаривает
по телефону.
Данное высказывание преобразуйте в эквивалентное, но уже не содержащее отрицаний сложных высказываний: Решение.

Упростите:
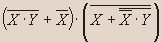 Решение.
Решение.