ВЫСШАЯ МАТЕМАТИКА
1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Сформулировать определения:
1) Дифференциальное уравнение первого порядка.
Уравнение F(x, y, y ') = 0, связывающее между собой независимую переменную, искомую функцию y(x) и ее производную y'(x) называется дифференциальным уравнением первого порядка.
F(x, y, y ') = 0 или y' = ƒ(x,y).
2) Интегральная кривая.
Решением(интегралом) дифференциального уравнения первого порядка является любая функция y = ϕ(x), которая при подстановке обращает его в верное тождество.
Интегральная кривая - график решения дифференциального уравнения(y = ϕ(x)).
Процесс нахождения решения дифференциального уравнения называется интегрированием.
3) Частное решение дифференциального уравнения первого порядка.
Частное решение(частный интеграл) дифференциального уравнения первого порядка называется решение общего интеграла при конкретном значении С. Частное решение находится, если задано начальное условие y(x0) = y0.
Каждому частному решению соответствует одна интегральная кривая, проходящая через точку x0,y0.
4) Общее решение дифференциального уравнения первого порядка.
Общим решением дифференциального уравнения первого порядка называется функция y = ϕ(x, C), где С - произвольная постоянная.
5) Общий интеграл дифференциального уравнения первого порядка.
Общее решение, записанное в неявном виде: Ф(x,y,C) = 0 - общий интеграл дифференциального уравнения первого порядка.
6) Задача Коши.
Задача Коши - нахождение частного решения или частного интеграла соответствующего заданному начальному условию F(x, y, y ') = 0.
7) Дифференциальное уравнение первого порядка в полных дифференциалах.
Дифференциальное уравнение первого порядка в полных дифференциалах называется уравнение вида: P(x,y)dx+Q(x,y)dy = 0, если существует такая функция двух переменных u(x,y) с частными производными, что справедливо выражение dU(x,y) = P(x,y)dx+Q(x,y)dy. Общее решение уравнения: u(x,y) = C.
Дифференциальное уравнение P(x,y)dx + Q(x,y)dy = 0 будет являться уравнением в полных дифференциалах тогда и только тогда, если справедливо равенство: dQ/dx = dP/dy.
8) Однородное дифференциальное уравнение первого порядка.
Однородное дифференциальное уравнение первого порядка - это уравнения вида y' = ƒ(x/y), P(x,y)dx+Q(x,y)dy = 0, где P(x,y) и Q(x,y) - однородные функции одинаковой степени.
9) Линейное дифференциальное уравнение первого порядка.
Линейное дифференциальное уравнение первого порядка - это уравнения вида y'+p(x)y = g(x), где p(x) и g(x) - непрерывные функции.
10) Линейное дифференциальное уравнение второго порядка.
Линейное дифференциальное уравнение второго порядка - это уравнение вида y'' + p(t)y'+q(t)y = r(t), где p(t), q(t), r(t) - непрерывные функции.
11) Характеристическое уравнение.
Если имеется однородное линейное дифференциальное уравнение c постоянными коэффициентами р0у(n) + p1y(n-1) + … + pny = 0, то алгебраическое уравнение p0λn + p1λn-1 + … + pn = 0
называется его характеристическим уравнением.
Сформулировать теоремы и свойства:
1) Теорема о существовании и единственности решения задачи Коши.
Уравнение
y'
= ƒ(x,y)
функция ƒ(x,y)
и ее частная производная
непрерывны в некоторой области D
плоскости Oxy.
Тогда для любой точки M(x0,y0)
D
существует единственное решение y
= y(x)
этого уравнения, удовлетворяющее
начальному условию y(x0)
= y0.
2) Правило решения дифференциальных уравнений первого порядка с разделяющимися переменными.
y'
= ƒ(x,y)
= p(x)q(y),
при y'
= dy/dx
=> dy/dx
= p(x)q(y)
=> dy/q(y)
= p(x)dx
=>
=> Q(y)
= P(x)
+ C.
3) Правило решения линейных дифференциальных уравнений первого порядка.
Метод Бернулли: y = uv, где u = u(x), v = v(x) - неизвестные функции по х.
y'=u'v+v'u. Подставляем в исходное уравнение. Делаем удобным для решения, одну из скобок приравниваем к нулю и находим или u, или v. Делаем обратную подстановку находим противоположное значение(u или v). Находим y.
4) Правило решения однородных дифференциальных уравнений первого порядка.
y' = ƒ(y/x), где y/x = u => y = ux. Дальше подставляем и интегрируем.
5) Правило решения дифференциальных уравнений первого порядка в полных дифференциалах.
Имеем dU(x,y) = P(x,y)dx+Q(x,y)dy . Смотрим выполняется ли равенство через частные производные dQ/dx = dP/dy. Находим dU/dx = P(x,y) и dU/dy = Q(x,y). Интегрируем dU/dx = P(x,y)считая y постоянным. Получаем некое выражение вида U(x,y) = P(x,y)+ϕ(y). Продифференцировав полученное равенство по y и учитывая второе равенство(dU/dy = Q(x,y)) получим dU/dy = P(x,y)+ϕ'(y)=Q(x,y), откуда получаем ϕ'(y), т.е ϕ(y) = некое выражение + C1. Общим интегралом является соотношение U(x,y) = P(x,y)+некое число + С1 = С2, или U(x,y) = P(x,y)+некое число = С.C находится подстановкой начального условие в уравнение.
6) Правило решения дифференциальных уравнений высшего порядка, допускающих понижение порядка.
Имеем
уравнение вида y''
= ƒ(x),
тогда решением является последовательное
интегрирование
,
.
7) Теорема о структуре общего решения линейного однородного дифференциального уравнения второго порядка.
Общее решение y00 линейного однородного дифференциального уравнения имеет вид y00 = C1y1(x)+C2y2(x), где y1(x) и y2(x) - линейно независимые решения этого уравнения.
8) Теорема о структуре общего решения линейного неоднородного дифференциального уравнения второго порядка.
Общее решение неоднородного дифференциального уравнения есть сумма какого-либо его частного решения и общего решения соответствующего ему однородного уравнения: y = y00 + ӯ, где ӯ - частное решение дифференциального уравнения, а y00 - общее решение дифференциального уравнения.
Доказательство теоремы для уравнения второго порядка y''+p*y'+q*y = ƒ(x), где p, q - константы.
y00 = c1*y1 + c2*y2 - общее решение для y''+p*y'+q*y = 0
(y00''+p*y00'+q*y00)+( ӯ''+p*ӯ'+q*ӯ) = ƒ(x)
Первая скобка - общее решения для y''+p*y'+q*y = 0, вторая скобка - частное решение для y''+p*y'+q*y = ƒ(x).
Частное решение находится двумя способами: методом неопределенных коэффициентов и методом вариаций.
9) Правило решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами.
y''+p*y'+q*y = 0 - общий вид уравнения.
k2+p*k+q = 0 - характеристическое уравнение.
Находятся корни характеристического уравнения, т.е. k1 и k2.
1. Если корни действительные числа и не равны, то общее решение: y = C1*ek1*x+ C2*ek2*x.
2. Если корни действительные числа и равны, то общее решение: y = ek1*x*(C1+C2*x).
3. Если корни комплексные числа (k1,2 = α+-jβ), то общее решение: y = eα*x*(C1*cos β*x+C2*cos β*x).
10) Правило решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами и правой частью специального вида.
y''+p*y'+q*y = ƒ(x), необходимо найти частное решение дифференциального уравнения.
Первый метод. ƒ(x) = eα*x*Pn(x), где Pn(x) - многочлен степени n.
а) Если α не является корнем уравнения k2+p*k+q = 0, то частное решение(ӯ) находится в виде
ӯ = eα*x*Qn(x), где Qn(x) - многочлен степени n с неизвестными коэффициентами.
б) Если α - корень уравнения k2+p*k+q = 0 кратности k, то: ӯ = xk*eα*x*Qn(x).
Второй метод. ƒ(x) = eα*x*[Pn(x)*cosβ*x+ Qm(x)*sinβ*x], где Pn и Qm - многочлены степени n и m. N = max(n,m).
а) Если α+-jβ не являются корнями уравнения k2+p*k+q = 0, то ӯ = eα*x*[PN(x)*cosβ*x+ QN(x)*sinβ*x].
б) Если α+-jβ корни уравнения k2+p*k+q = 0 кратности k, то ӯ = xk*eα*x*[PN(x)*cosβ*x+ QN(x)*sinβ*x].
2. ЧИСЛОВЫЕ РЯДЫ. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ. ПРИЗНАКИ СХОДИМОСТИ.
Сформулировать определения:
1) Числовой ряд.
Числовой
ряд - это сумма
членов числовой последовательности
вида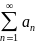 
или
a1+a2+a3+a4...aк
+...
2) Частичная сумма ряда.
Суммы вида: S1 = a1, S2 = a1+a2, S3 = a1+a2+a3 и т.д., называются частичными суммами ряда.
3) Сумма ряда.
Суммой
сходящегося числового ряда
называется предел
последовательности его частичных сумм,
т.е.
=
S
4) Сходящийся и расходящийся числовой ряд.
Числовой ряд называется сходящимся, если существует конечный предел последовательности {Sn} его частичных сумм: S = .
Если данного предела не существует или он равен бесконечности, то числовой ряд называется расходящимся и суммы не имеет.
5) Остаток ряда.
Ряд,
полученный отбрасыванием от исходного
n
первых членов, называется n-м
остатком ряда.
rn=
Сформулировать теоремы и свойства:
1) Необходимое условие сходимости ряда.
Если
ряд
сходится,
то
=0,
иначе расходится.
2) Критерий Коши сходимости числового ряда.
Пусть задана числовая последовательность {xn}. Эта последовательность сходится тогда и только тогда, когда для любого числа ε > 0 существует номер N такой, что при всех n > N и любых натуральных m выполняется неравенство (т.е. расстояние между членами последовательности с номерами n и n+m меньше ε) – критерий Коши сходимости последовательности.
3) Критерий сходимости ряда с положительными членами.
= 0 => сходится, иначе расходится.
4) I критерий сравнения.
Если
начиная с некоторого номера N
для всех n>N
выполняется неравенство an≤bn,
то из сходимости
ряда
следует сходимость ряда
,
а из расходимости ряда
следует расходимость ряда
.
5) II(предельный) признак сравнения.
Если
существует конечный предел
(an/bn)=k≠0,
то ряды
и
либо оба сходятся либо оба расходятся.
6) Признак сходимости Даламбера.
Пусть
дан положительный ряд
и существует конечный
предел
=L.
Тогда если L<1,то
данный ряд сходится, если L>1,
то расходится, если L=1,то
ряд может сходиться или расходиться. В
этом случае требуется исследовать ряд
с помощью других методов.
7) Радикальный признак Коши.
Пусть
–
положительный числовой ряд (an>0)
и существует конечный предел
=
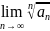K,
тогда если 0≤К<1,то
данный ряд сходится, если К>1,
то расходится, если К=1,
то ряд может сходиться
или расходиться. В этом случае требуется
исследовать ряд с помощью других методов.
8) Интегральный признак Коши.
Пусть
-ряд
с положительными членами, для которого
существует положительная, непрерывная
и монотонно убывающая на промежутке
[1,+∞)
функция ƒ(x),такая
что ƒ(n)
= an,
n
= 1,2,... ,тогда ряд
и
несобственный интеграл
сходятся
или расходятся одновременно.
3. РЯДЫ С ПРОИЗВОЛЬНЫМИ ЧЛЕНАМИ. АБСОЛЮТНАЯ И УСЛОВНАЯ СХОДИОМСТЬ.
Сформулировать определения:
1) Знакочередующийся ряд.
Ряд,
в котором любые два соседних члена имеют
разные знаки, т.е. знакочередующийся
ряд - это ряд вида: a1-a2+a3-a4+…+(-1)n+1
an
+… =
или -a1+a2-a3+a4+…+(-1)n
an
+… =
,
где все an
- положительные действительные числа
(an>0,
n
= 1,2,3....).
2) Знакопеременный ряд.
Ряд, содержащий и положительные и отрицательные члены, называется знакопеременным. В частности, всякий знакочередующийся ряд является знакопеременным.
3) Абсолютно и условно сходящийся ряд.
Пусть
дан знакопеременный
ряд, где an
– произвольные
числа (действительные или комплексные).
Если ряд
,
составленный из абсолютных величин его
членов сходится, то данный ряд
также сходится. В
этом случае знакопеременный ряд
называется абсолютно
сходящимся.
Если ряд сходится, а ряд расходится, то данный ряд называется условно сходящимся.
Сформулировать теоремы и свойства:
1) Теорема Лейбница.
Знакочередующийся
ряд S=
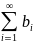сходится, если выполняется условие
и
bi=0.
2) Достаточный признак сходимости знакопеременного ряда.
Если
сходится ряд
,
то сходится и ряд
.
4. ФУНКЦИОНАЛЬНЫЕ РЯДЫ. СТЕПЕННЫЕ РЯДЫ. РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ.
Сформулировать определения:
1) Функциональный ряд.
Функциональный
ряд - ряд, каждым
членом которого является не число, а
функция uk(x).
u1(x)+u2(x)+...un(x)+...
=
.
2) Область сходимости функционального ряда.
Множество всех значений переменной Х, при которых степенной ряд сходится, называется областью сходимости ряда.
3) Сумма функционального ряда.
Если значение х0 переменной х принадлежит области сходимости функционального ряда , то можно говорить о сумме этого функционального ряда в точке х = x0: u1(x0) + u2(x0) + ... + u2(x0) + un(x0) + ... =S(x0).
Таким образом, значение суммы функционального ряда зависит от значения x0 переменной х, т.е. сумма функционального ряда сама является функцией переменной х. Областью определения суммы функционального ряда является область сходимости этого ряда.
4) Равномерно сходящийся функциональный ряд.
Функциональный
ряд u1(x)+u2(x)+...un(x)+...
=
называется равномерно
сходящимся в
некоторой области Х,
если для любого малого числа Ɛ
0
можно указать такое целое число N(Ɛ)
0, зависящее только
от Ɛ
и не зависящая от х,
что при всех n
N(Ɛ)
неравенство
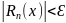выполняется для всех х
из области Х.
5) Степенной ряд.
Степенной
ряд - ряд вида
a0+a1*x+a2*x2+...+an*xn+...
или
.
6) Радиус сходимости степенного ряда.
Интервалом сходимости степенного ряда называется интервал (-R, R), в каждой точке которого ряд сходится, а вне интервала - расходится. На границах интервала сходимости, т.е. в точках х = +-R, интервал может как сходится, так и расходиться. R - радиус сходимости ряда.
Вычисление радиуса сходимости:
(по
Дамблеру) R
=
(по
Коши) R
=
7) Ряд Тейлора.
Ряд Тейлора - разложение функции в бесконечную сумму степенных функций.
ƒ(x)
бесконечно дифференцируема в некоторой
окрестности точки α,
тогда ряд вида
называется рядом
Тейлора функции ƒ
в точке α.
8) Ряд Маклорена.
Если
в ряде Тейлора
α = 0,
то ряд называется рядом
Маклорена.
Сформулировать теоремы и свойства:
1) Признак Вейерштрасса равномерной и абсолютной сходимости.
Функциональный
ряд, каждый член которого является
функцией, определенной в некоторой
области D,
сходится равномерно в этой области,
если существует такая последовательность
с1,
с2,...,
сn,...
положительных
постоянных, что выполняется неравенство
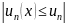для любого х
D
и любого n
= 1, 2, 3..., а ряд
с1+с2+...+сn+...
сходится.
2) Свойства равномерно сходящихся рядов.
1. Сумма S(x) равномерно сходящегося ряда в области Х, где un(x) (n = 1, 2, 3...) - непрерывные функции, является непрерывной функцией в области Х.
2.
Равномерно сходящийся ряд
,
где un(x)
(n
= 1, 2, 3...) можно
почленно интегрировать, т.е.
3.
Если ряд, составленный из производных
сходящегося ряда
,
сходится равномерно, то исходный ряд
можно почленно дифференцировать.
3) Теорема Абеля.
Если
степенной ряд
сходится в точке х0,
то он абсолютно сходится в каждой точке
х,
для которой
.
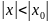4) Способы отыскания интервала и радиуса сходимости степенного ряда.
Вычисление радиуса сходимости:
(по Дамблеру) R =
(по Коши) R =
Интервал сходимости степенного ряда представляется в виде (х0-R, x0+R).
5) Свойства степенных рядов.
1.
Сумма степенного ряда
представляет собой функцию, определенную
и непрерывную в интервале сходимости
(-R,
R).
2. Степенной ряд можно почленно дифференцировать внутри интервала сходимости.
3. Степенной ряд можно почленно интегрировать на каждом отрезке, отложенном внутри интервала сходимости.
6) Условие разложимости функции в ряд Тейлора.
Для
того чтобы функция f(x) могла быть разложена
в степенной ряд на интервале (−R, R),
необходимо, чтобы эта функция имела
производные любого порядка для x ∈
(−R, R) и существовал
.
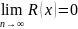7) Разложение основных элементарных функций в ряд Маклорена: ƒ(x) = ex, ƒ(x) = sin x, ƒ(x) = cos x, ƒ(x) = (1+x)a, ƒ(x) = ln(1+x), ƒ(x) = arctg x.
.
.
.
.
.
.
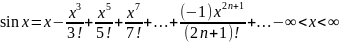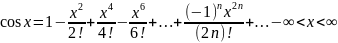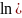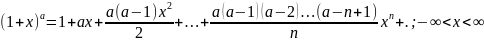5. РЯДЫ ФУРЬЕ.
Сформулировать определения:
1) Тригонометрический ряд.
Тригонометрический
ряд - любой ряд вида
.
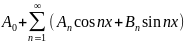Не каждый тригонометрический ряд является рядом Фурье.
2) Ряд Фурье.
Ряд
Фурье - ряд вида
.
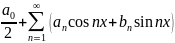Тригонометрический ряд называется рядом Фурье, если коэффициенты An и Bn определяются следующим образом:
.
Сформулировать теоремы и свойства:
1) Разложение функций в ряд Фурье на промежутке [-π, π].
Если функция ƒ(x) непрерывна или имеет конечное число точек разрыва на отрезке [-π;π] и при этом монотонна или имеет конечное число экстремумов на [-π;π], то ряд Фурье функции ƒ(x) сходится для любых х из [-π;π] и его сумма равна:
1. ƒ(x) для всех точек непрерывности х интервала (-π;π).
2.
для всех точек разрыва х0.
3.
при х = -π
и х = π.
2) Разложение четных и нечетных функций в ряд Фурье на промежутке [-π, π].
Четная:
ƒ(x)
=
,
где
,
.
Нечетная:
ƒ(x)
=
,
где
.
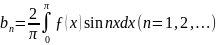3) Разложение функций в ряд Фурье в произвольном интервале.
,
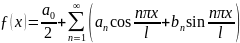где
,
,
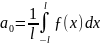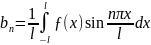(n
= 1, 2,...).
Четный ряд раскладывается по косинусам, нечетным - по синусам.
6. ДВОЙНОЙ ИНТЕГРАЛ: ОПРЕДЕЛЕНИЕ, СВОЙСТВА, ВЫЧИСЛЕНИЕ, ПРИЛОЖЕНИЕ.
Сформулировать определения:
1) Двойной интеграл
Двойным интегралом от функции ƒ(x,y) по ограниченной замкнутой области D называется предел интегральной суммы, построенной для функции ƒ(x, y) при неограниченном разбиении области D на ячейки и при стягивании каждой ячейки в одну точку.
.
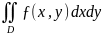Сформулировать теоремы и свойства:
1) Теорема о существовании двойного интеграла.
Если функция ƒ(x,y) непрерывна в заданной области D, то двойной интеграл существует.
2) Геометрический смысл двойного интеграла.
Если
ƒ(x,y)
0
и непрерывна в области D,
то интеграл
выражает объем тела, ограниченного
снизу областью D,
сверху - поверхностью z
= ƒ(x,y),
а с боков - цилиндрической поверхностью,
образующие которой параллельны оси Oz.
3) Физический смысл двойного интеграла.(???)
Физический смысл определяется физическим смыслом интегрируемой функции, т.е. (???)
4) Свойства двойных интегралов.
1.
Линейность:
.
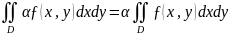2.
Монотонность:
,
т.е. можно почленно интегрировать.
3.
Аддитивность:
.
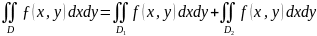4.
.
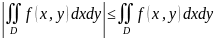5.
Теорема о среднем: Если функция ƒ(x,
y)
непрерывна в области D,
то существует точка М0(х0,
у0),
такая, что
.
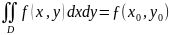5) Вычисление двойных интегралов в прямоугольных, декартовых координатах.
.
6) Вычисление двойных интегралов в полярных координатах.
.
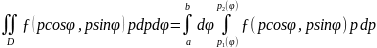7) Приложение двойных интегралов.
1.
Объем тела: V
=
,
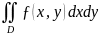где z
= ƒ(x,y)
- уравнение поверхности, ограничивающей
тело сверху.
2.
Площадь плоской фигуры:
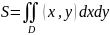- декартовая система координат,
- полярных координатах.
3.
Масса плоской фигуры:
.
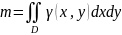4. Статистические моменты:
- относительно оси Ох.
- относительно оси Оу.
5. Момент инерции
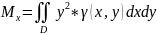- относительно оси Ох.
- относительно оси Ох.
7. ТРОЙНОЙ ИНТЕГРАЛ: ОПРЕДЕЛЕНИЕ, СВОЙСТВА, (НИНА) ВЫЧИСЛЕНИЕ.
Сформулировать определения:
1) Тройной интеграл.
Тройным интегралом от функции ƒ(x,y,z) по области U называется конечный предел интегральной суммы при стремлении к нулю наибольшего из диаметров частичных областей.
.
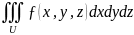Сформулировать теоремы и свойства:
1) Теорема о существовании тройного интеграла.
Если функция ƒ(x,y,z) непрерывная в замкнутой области V, то существует.
2) Физический смысл тройного интеграла.
Масса
тела переменной плотности γ
= f(x,y,z):
M
=
.
Объем: V
=
.
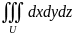3) Свойства тройных интегралов.
1.
Линейность:
.
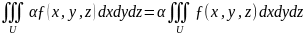2.
Монотонность:
,
т.е. можно почленно интегрировать.
3.
Аддитивность:
4.
.
5.
Теорема о среднем: Если функция ƒ(x,
y,
z)
непрерывна в области U,
то существует точка М0(х0,
у0,
z0),
такая, что
.
4) Вычисление тройных интегралов в прямоугольных декартовых координатах.
.
5) Вычисление тройных интегралов в цилиндрических координатах.
.
x = p*cosϕ, y = p*sinϕ, z=z
6) Вычисление тройных интегралов в сферических координатах.
.
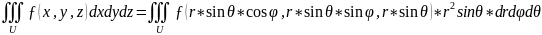x = r*sinθ*cosϕ, y = r*sinθ*sinϕ, z = r*cosθ.
7) Приложения тройных интегралов.
1.
Объем тела:
.
2. Масса тела переменной плотности γ = f(x,y,z): M = .
3.
Координаты центра тяжести с постоянной
плотностью:
.
4.
Координаты центра тяжести с переменной
плотностью γ
= f(x,y,z):
.
7*. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ I и II РОДА.
Сформулировать определения:
1) Криволинейный интеграл I рода.
Криволинейным
интегралом первого рода
от скалярной функции F
вдоль кривой С
называется интеграл
вида
,
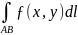где l
- длина дуги.
2) Криволинейный интеграл II рода.
Криволинейным
интегралом второго рода
от векторной функции F
вдоль кривой С
называется интеграл вида
(полный
интеграл).
Сформулировать теоремы и свойства:
1) Условие существования криволинейного интеграла I рода.
Криволинейный интеграл существует, если функция F непрерывна на прямой С.
2) Физический смысл криволинейного интеграла I рода.
m
=
,
где p(плостность)
= p(x,y).
3) Геометрический смысл криволинейного интеграла I рода.
Если
функция f(x)
непрерывна и положительна на [a,
b],
то интеграл
представляет собой площадь криволинейной
трапеции, ограниченной линиями y
= 0, x = a, x = b, y = f(x).
4) Свойства криволинейных интегралов I рода.
1.
Линейность:
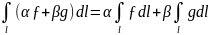
2.
Аддитивность:
если l1
l2
в одной точке, то
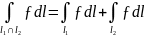
3.
Монотонность:
если ƒ
g
на
l,
то
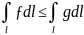
4. Криволинейный интеграл первого рода не зависит от параметризации кривой.
5) Вычисление криволинейного интеграла I рода.
Вычисление криволинейного интеграла 1-го рода сводится к вычислению обычного определенного интеграла от функции в заданных пределах.
6) Механический смысл криволинейного интеграла II рода.
Смысл криволинейного интеграла 2 рода – работа по перемещению тела вдоль кривой в поле переменных сил.
7) Свойства криволинейных интегралов II рода.
1.
Линейность:
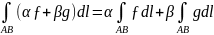
2.
Аддитивность:
3.
Монотонность:
если ƒ
g
на
l,
то
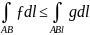
4.
Оценка
модуля:
8) Вычисление криволинейных интегралов II рода.
Кривая
L
задана в явном виде непрерывно
дифференцируемой функцией y
= y(x),
x
[a,b],
то
=
.
Кривая
L
задана параметрическими функциями x
= x(t),
y
= y(t),
t
[α,
],
то
.
9) Связь между криволинейными интегралами I и II рода.
,
где левая часть - интеграл второго рода,
правая - первого.
10) Формула Грина.
.
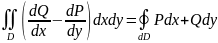11) Условия независимости криволинейного интеграла II рода от пути интегрирования.
Криволинейный
интеграл второго рода от векторной
функции не зависит от пути интегрирования,
если P,
Q
и R
являются непрерывными функциями в
области интегрирования D
и в этой области существует скалярная
функция u
= u(x,
y,
z),
такая, что
,
,
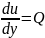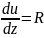
12) Приложения криволинейных интегралов I и II рода.
I род:
1.
Если подынтегральная функция равна
единице, то интеграл
.
2.
Площадь цилиндрической поверхности: S
=
.
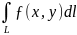3. Масса кривой: m = , где p(плостность) = p(x,y).
4. Статические моменты относительно осей Ох и Оу:
Мx
=
,
Мy
=
,
где p(x,y)
- плотность распределения кривой L,
а хс
= Му/m,
ус
= Мх/m
- координаты центра тяжести(центра масс)
кривой L.
5. Моменты инерции относительно осей и начала координат:
Jx
=
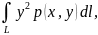Jy
=
Jx
=
II род:
1.
Работа, совершаемая
силой F(Fx,
Fy,
Fz),
действующей на точку при перемещении
ее по кривой L:
A
=
.