12) Достоверность передачи информации. Коды Хемминга.
Используют несколько приемов повышения надежности сообщений:
1. Повтор сообщений - простой способ повышения их достоверности. Предполагается, что в одном из посланных одинаковых сообщений символы будут не искажены. Сопоставляя сообщения, можно будет исправить ошибки.
Кодирование с выявлением ошибок (коды с проверкой на четность).
Увеличивая число дополнительных разрядов и формируя по определенным правилам проверочные
символы можно усилить корректирующие свойства кода так, чтобы он не только обнаруживал, но и
исправлял ошибки. Для исправления ошибки не достаточно установить ее наличие, нужно указать
позицию, в которой произошла ошибка.
Алгоритм построения кода с проверкой на четность.
Разбиваем сообщение на p слов, длиной n
Считаем контрольную сумму слова по модулю 2 каждого слова
Если контрольная сумма = 0, в дополнительный разряд ставим 0.
Если контрольная сумма = 1, в дополнительный разряд ставим 0
Передаем закодированное сообщение
Принимаем сообщение
Считаем контрольные суммы каждого полученного слова. если сумма совпадает с значением в дополнительном разряде – ошибки нет, иначе есть ошибка. При условии, что в слове сделано нечетное количество ошибок.
Приказываем передатчику повторить слово, в котором есть ошибка.
3. Кодирование с исправлением ошибок (самокорректирующиеся коды).
Самокорректирующиеся коды позволяют не только обнаруживать, произошла ли в блоке определенной длины ошибка при передаче сообщения, но и определять, в каких именно разрядах это случилось. После определения номера разряда, где произошла ошибка, коррекция сводится просто к изменению значения разряда (если в данном разряде записан нуль, то он изменяется на единицу, и наоборот).
Код Хемминга - простейший код, исправляющий одну ошибку.
В основу метода положено добавление к информационным битам добавочных битов проверки четности суммы знаков двоичной кодовой комбинации. Проверочные знаки расположены в разрядах, номера которых равны степеням числа 2: 1=20, 2=21, 4=22, 8=23,...
Алгоритм кодирования
Вычисляем количество разрядов, необходимое для передачи сообщения, закодированного кодом Хемминга
Количество информационных разрядов обозначим n.
Количество проверочных разрядов обозначим p.
Найдем число проверочных разрядов, оно должно быть таким, чтобы выполнялось следующее соотношение: p ≥ log2 (n + p+1)
Строим таблицу.
В первом столбце располагаем номера разрядов от 1 до 12
Выделяем среди разрядов проверочные и информационные.
Проверочные разряды будут располагаться в разрядах, номера которых равны степеням числа 2: 1=20, 2=21, 4=22, 8=23, …
Информационные разряды будут располагаться в разрядах с остальными номерами.
Во втором столбце записываем обозначения разрядов
Проверочные разряды обозначим y1, y2, y3, y4, информационные - x1, x2, x3, x4, x5, x6, x7, x8.
В третьем столбце записываем значения информационных разрядов.
В остальных столбцах записываем двоичные представления номеров разрядов.
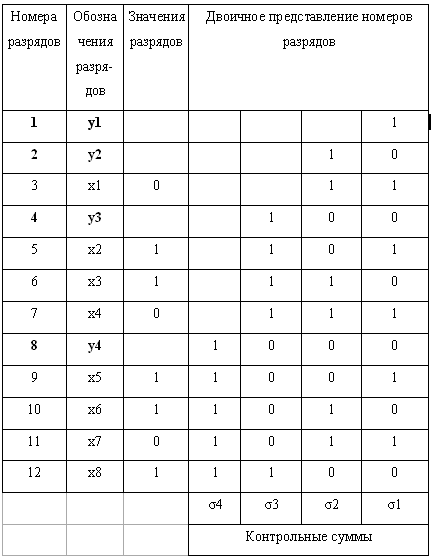
Найдем значения проверочных разрядов, вычисляя контрольные суммы (σ1, σ2, σ3, σ4).
Уравнения, для вычисления контрольных сумм составляются следующим образом: в i-ю контрольную сумму войдут значения разрядов, номера которых в двоичном представлении имеют единицу в i-ом разряде.
Запишем уравнения для контрольных сумм
Подставим в уравнения значения информационных разрядов и определим значения проверочных разрядов. Значения проверочных разрядов выбираются так, чтобы контрольная сумма по модулю 2 равнялась нулю. Получив значения проверочных разрядов, мы можем выписать код Хемминга
Двоичное число σ4 σ3 σ2 σ1, составленное из этих сумм, называют контрольным кодом.
Для построенного таким образом кода Хемминга с исправлением одной ошибки справедливо следующее предположение: если в коде Хемминга с исправлением одной ошибки возникла единственная ошибка в каком-либо разряде (неважно, в информационном или проверочном), то контрольный код будет совпадать с двоичным представлением номера разряда, в котором возникла ошибка.
Благодаря тому, что коды являются двоичными, знание разряда, в котором произошла ошибка, позволяет исправить эту ошибку. Для этого достаточно заменить цифру (0 или 1), стоящую в указанном разряде, на противоположную.