11) Кодирование информации. Условие Фано. Коды Шеннона-Фано и Хаффмана.
Кодом называют правило, описывающее отображение одного набора знаков в другой набор знаков.
Иногда кодом называют множество образов при этом отображении.
Кодирование информации. Слово «кодирование» понимается не в узком смысле — кодирование как способ сделать сообщение непонятным для всех, кто не владеет ключом кода, а в широком — как представление информации в виде сообщения на каком-либо языке. Правило отображения одного алфавита в другой.
Для представления информации в памяти ЭВМ (как числовой, так и не числовой) используется двоичный способ кодирования.
Элементарная ячейка памяти ЭВМ имеет длину 8 бит (байт). Каждый байт имеет свой номер (его называют адресом). Наибольшую последовательность бит, которую ЭВМ может обрабатывать как единое целое, называют машинным словом. Длина машинного слова зависит от разрядности процессора и может быть равной 16, 32 битам и т.д.
Для кодирования символов достаточно одного байта. При этом можно представить 256 символов (с десятичными кодами от 0 до 255). Набор символов персональных ЭВМ IBM PC чаще всего является расширением кода ASCII (стандартный американский код для обмена информацией).
Другой способ представления целых чисел — дополнительный код. Диапазон значений величин зависит от количества бит памяти, отведенных для их хранения. Например, величины типа Integer лежат в диапазоне от –32768 (–215) до 32767 (215 – 1) и для их хранения отводится 2 байта; типа LongInt — в диапазоне от –231 до 231 – 1 и размещаются в 4 байтах; типа Word — в диапазоне от 0 до 65535 (216 – 1) (используется 2 байта) и т.д.
Данные могут быть интерпретированы как числа со знаками, так и без знаков. В случае представления величины со знаком самый левый (старший) разряд указывает на положит. число, если содержит нуль, и на отрицат., если — единицу.
Вообще, разряды нумеруются справа налево, начиная с 0.
Дополнительный код положительного числа совпадает с его прямым кодом. Прямой код целого числа может быть получен следующим образом: число переводится в двоичную систему счисления, а затем его двоичную запись слева дополняют таким количеством незначащих нулей, сколько требует тип данных, к которому принадлежит число.
Дополнительный код целого отрицательного числа может быть получен по следующему алгоритму:
1) записать прямой код модуля числа;
2) инвертировать его (заменить единицы нулями, нули — единицами);
3) прибавить к инверсному коду единицу.
При получении числа по его дополнительному коду прежде всего необходимо определить его знак. Если число окажется положительным, то просто перевести его код в десятичную систему счисления. В случае отрицательного числа необходимо выполнить следующий алгоритм:
1) вычесть из кода числа 1;
2) инвертировать код;
3) перевести в десятичную систему счисления. Полученное число записать со знаком минус.
Несколько иной способ применяется для представления в памяти персонального компьютера действительных чисел - формат с плавающей точкой.
Формат чисел с плавающей точкой основывается на нормализованной форме записи чисел.
НФЗ в десятич сист счисл:
А = М ∙ 10 p, где М – мантисса числа (1 £ M < 10), p — порядок числа (целое число).
НФЗ в двоич сист счисл:
А = 1,М ∙ 2 p, M — мантисса (ее целая часть равна 1(2)) и p — порядок, записанный в десятичной системе счисления.
Число в форме с плавающей точкой может занимать в памяти компьютера 4 (число обычной точности - Single) или 8 (число двойной точности - Double) байтов. В памяти хранятся: знак числа, значение мантиссы числа и значение порядка.
Алгоритм для получения представления действительного числа в памяти ЭВМ:
1) перевести модуль данного числа в двоичную систему счисления;
2) нормализовать двоичное число, т.е. записать в виде M × 2p, где M — мантисса (ее целая часть равна 1(2)) и p — порядок, записанный в десятичной системе счисления;
3) прибавить к порядку смещение и перевести смещенный порядок в двоичную систему счисления;
4) учитывая знак заданного числа (0 — положительное; 1 — отрицательное), выписать его представление в памяти ЭВМ.
Вся информация в компьютере закодирована равномерными кодами.
Равномерный – каждому символу соответствует кодовое слово одинаковой длины: а – 000, в – 001, с – 010.
Сообщение, записанное на естественном языке обладает избыточностью.
Коэф. избыточности
Неравномерный - каждому символу соответствует кодовое слово не одинаковой длины.
Закодированные неравномерным кодом сообщения могут декодироваться благодаря свойству префиксности эффективных кодов - Условие Фано: никакое кодовое слово не является началом другого кодового слова.
Код Шеннона - Фано достаточно хорошо удовлетворяет условию равной встречаемости символов 0 и 1 в закодированном сообщении.
Идея кодирования состоит в следующем.
1) Все кодируемые символы сортируются по убыванию вероятности появления.
2) Все символы разделяются на две группы так, чтобы выполнялось условие: суммарно символы из каждой группы встречаются одинаково часто (то есть вероятность того, что в сообщении встретится символ, принадлежащий к первой группе, равна вероятности того, что в сообщении встретится символ из второй группы).
3) Первому разряду кода символов первой группы присваивается значение 0, первому разряду кода символов второй группы - 1.
4) Далее для каждой из 2х групп выполняются шаги 1)-3)
Процесс разбиения символов на группы и кодирования продолжается до тех пор, пока в подгруппах не остается по одному символу.
Код Хаффмана
Этот метод имеет два преимущества по сравнению с методом Шеннона-Фано: он устраняет неоднозначность кодирования, возникающую из-за примерного равенства сумм частот при разделении списка на две части (линия деления проводится неоднозначно), и имеет, в общем случае, большую эффективность кода.
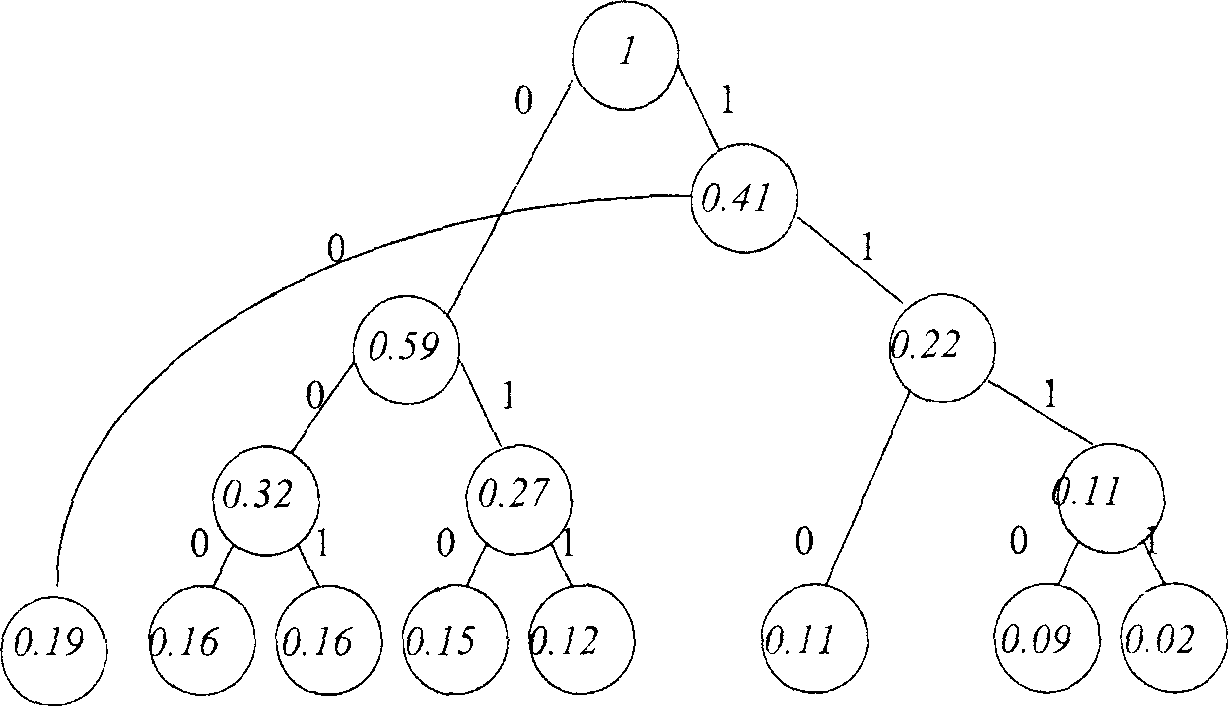
Строится кодовое дерево. Построение графа начинается с висячих вершин. Их число соответствует количеству символов в алфавите. Вес каждой вершины – это есть вероятность появления соответствующего символа. Перед началом работы висячие вершины упорядочиваются по мере увеличения вероятности. Шаг 1: определяется число поддеревьев графа. Если оно меньше 2, то дерево построено, если нет – шаг 2.
Шаг 2: выбирается 2 вершины с минимальными весами и сращиваются. Получается новая вершина и 2 ребра. Новая вершина имеет вес = сумме исходных вершин. Левое ребро получается 0, правое – 1. Возврат к шагу 1.
В результате построения дерева получается корень всегда = 1.
Чтобы получить кодовую комбинацию i-го символа необходимо от корня дерева спустится по ребрам к i-ой висячей вершине, выписав при этом метки ребер этого пути.
