№9

1. Деформация — изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформировать тело —смещать составляющие его частицы относительно друг друга. Виды деформации: растяжение-сжатие,сдвиг,изгиб,кручение. Сила упругости — сила, возникающая при деформации тела и противодействующая этой деформации. В простейшем случае одномерных малых упругих деформаций формула для силы упругости имеет вид: (закон Гука) (с минусом перед k),где k — жёсткость тела, дельтаX — величина деформации. Сила, препятствующая скольжению соприкасающихся тел друг относительно друга, называется силой трения. Она направлена по касательной к поверхности соприкосновения тел противоположно скорости скольжения данного тела (трение скольжения). Трение существует и в случае неподвижных относительно друг друга тел (трение покоя). Fтp = kN (сила трения Frp пропорциональна силе N, прижимающей сопри-касающиеся тела друг к другу (т. е. силе нормального давления)

2. Будем искать выражение в общем виде для внешней работы, которую совершает газ при изменении его объема. Рассмотрим, например, газ, который находится под поршнем в цилиндрическом сосуде (рис. 1). Если газ, расширяясь, передвигает поршень на бесконечно малое расстояние dl, то он осуществляет над ним работу   где S — площадь поршня, Sdl=dV— изменение объема газа. Таким образом, 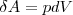  (1)  Полную работу А, которую совершает газ при изменении его объема от V₁ до V₂, найдем интегрированием формулы (1): 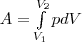  (2) Результат интегрирования зависит от вида зависимости между давлением и объемом газа. Найденное для работы выражение (2) справедливо при любых изменениях объема твердых, жидких и газообразных тел.  Осуществленную в том или ином процессе работу можно изобразить графически с помощью кривой в координатах р, V. Пусть, например, изменение давления газа при его расширении изображается кривой на рис. 2. При увеличении объема на dV совершаемая газом работа равна pdV, т. е. определяется площадью полоски с основанием dV, которая заштрихована на рисунке. Значит полная работа, которая совершается газом при расширении от объема V₁ до объема V₂, определяется площадью, ограниченной осью абсцисс, кривой p=f(V) и прямыми V₁ и V₂. 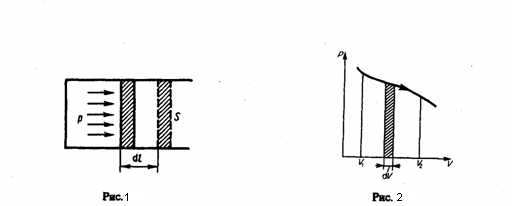 Графически можно представлять только равновесные процессы — процессы, которые состоят из последовательности равновесных состояний. Они протекают таким образом, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессы не являются равновесными (они протекают с конечной скоростью), но в ряде случаев неравновесностью реальных процессов можно пренебречь (чем медленнее протекает процесс, тем он ближе к равновесному). В классической термодинамике рассматриваемые процессы предполагаются равновесными. 

• Помимо удельной теплоемкости с вещества введем понятие молярной теплоемкости См-

Молярной теплоемкостью называется количество теплоты, не¬обходимое для нагревания моля вещества на I К. Из определения удельной теплоемкости (см. § 39) следует, что она связана с молярной соотношением

См = Мс,

где М — молярная масса вещества. Единицей См является джоуль на келъвин-моль (Дж/(К-моль)

Молярной теплоемкостью при постоянном объеме называется к< личество теплоты, необходимое для нагревания моля газа на 1 при постоянном объеме.

Cv = дельта U м / дельта Т дельтаUM = iR * AT/2 Су = iR/2 Молярной теплоемкостью при постоянном давле- * HULL называется количество теплоты, необходимое] для нагревания моля газа на 1 К при постоянном давлении.

• МАЙЕРА УРАВНЕНИЕ - ур-ние, устанавливающее связь между теплоёмкостями при пост, давлении Cp и пост, объёме С_V 1 кмоляидеального газа:  где R - газовая постоянная .Впервые было получено Ю. P. Майером (J. R. Mayer) в 1842 и ещё до работ Дж. П. Джоуля (J. P. Joule) использовано им для количеств, определения механического эквивалента теплоты. Для произвольной массы т(кг) вещества в состоянии идеального газа M. у. 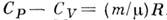записывается в виде:   , где 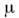 - молекулярная масса газа. M. у. можно получить из общего соотношения 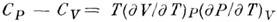  (см. Термодинамика ),если учесть, что для идеального газа справедливо Клапейрона уравнение. Cp=CV+R — уравнение Майера

3. Опыт и теория показывают, что все вещества, помещенные в магнит¬ное тле, приобретают магнитные свойства, т. е. намагничиваются, и потому в некоторой мере изменяют внешнее (первоначальное) поле. При этом оказывается, что одни вещества ослабляют внешнее поле, а другие — усиливают его; первые называются диамагнитными, вторые — парамагнитными веществами, или, короче, диамагнетиками и парамагнетиками. Среди парамагнетиков резко выделяется груши» веществ, вызывающих очень большое усиление внешнего поля. »гм вещества называются ферромагнетиками.

Подавляющее большинство веществ относится к диамагнетикам. Диамагнетиками являются такие элементы, как фосфор, сера, сурьмя, углерод, многие металлы (висмут, ртуть, золото, серебро, медь и др ). большинство химических соединений (в том числе вода и почти тс органические соединения). К парамагнетикам относятся некоторые газы (кислород, азот) и металлы (алюминий, вольфрам, платина, щелочные и щелочноземельные металлы). В довольно малочисленную группу ферромагнетиков входят железо, никель, кобальт, гадолиннй и диспрозий, а также некоторые сплавы и окислы этих металлов и некоторые сплавы марганца и хрома.

• Намагни́ченность — векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычно М или J. Определяется как магнитный момент единицы объёма вещества:

Здесь, M — вектор намагниченности; m - вектор магнитного момента; V — объём.

• Если в ферромагнетике, намагниченном, например, до состояния Насыщения Вмакс, начнет уменьшаться напряженность H поля, то

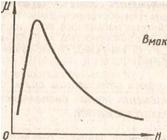
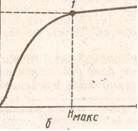
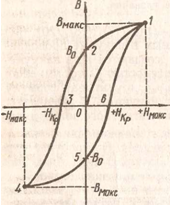
индукция В тоже будет уменьшаться; однако ее уменьшение происходит не по линии 10, а по линии 12 графика намагничивания (рис. 94).

При Н — О ферромагнетик не размагничивается полностью: в нем сохраняется остаточная магнитная индукция В*o . Для его полного

необходимо создать противоположное внешнее поле напряженностью H = — Hкр; эта напряжен¬ность называется коэрцитивной силой. При дальнейшем увеличении противоположного поля ферромагнетик начнет перемагничиваться (линия 34) и при Я = — Ямакс намагнитится до насыщения в противоположном направлении (В = — Вмакс). Затем ферромагнетик можно опять размагнитить (линия 456) и вновь перемагнитить до насыщения Вмакс (линия 61). Рассмотренное явление отставания изменений магнитной индукции от изменений напряженности намагничивающего поля называется магнитным гистерезисом, а замкнутая кривая 12451 — петлей гистерезиса.

Площадь, ограниченная петлей ги-стерезиса, характеризует работу, затраченную внешним полем на однократное перемагничивание ферромагнетика. Эта работа выделяется в виде теплоты.

№10 1. Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:

Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной

G = 6,67·10–11 Н·м2/кг2 (СИ).

Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все они находят объяснение на основе закона всемирного тяготения и законов динамики.

Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если M – масса Земли, R_З – ее радиус, m – масса данного тела, то сила тяжести равна 

где g – ускорение свободного падения у поверхности Земли: 

Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с². Зная ускорение свободного падения и радиус Земли (R_З = 6,38·10⁶ м), можно вычислить массу Земли М: 

При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Рис. 1.10.2 иллюстрирует изменение силы тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт притягивается к Земле вблизи ее поверхности, принята равной 700 Н.

• Сила, с которой тело притягивается к Земле, называется силой тяжести.

Вес — сила воздействия тела на опору (или подвес или другой вид крепления), препятствующую падению, возникающая в поле сил тяжести. Вес тела равен силе, с которой неподвижное относительно Земли и находящееся в пустоте тело давит на горизонтальную опору или растягивает пружину вследствие притяжения к Земле.

Невесо́мость — состояние, при котором сила взаимодействия тела с опорой (вес тела), возникающая в связи с гравитационным притяжением, действием других массовых сил, в частности силы инерции, возникающей при ускоренном движении тела, отсутствует.

2. Адиабати́ческий, или адиаба́тный проце́сс — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством .

Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии, то адиабатический процесс в силу отсутствия теплообмена ( ) системы со средой сводится только к последним двум процессам. Поэтому, первое начало термодинамики в этом случае приобретает вид

где   — изменение внутренней энергии тела,   — работа, совершаемая системой.

Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит^[8]:

Здесь   — температура системы,   — теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла.

• Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает

электростатическое поле,стационарное поле температуры,поле давления,поле потенциала скорости в гидродинамике.

Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.

Это уравнение имеет вид: 

где   — оператор Лапласа или лапласиан, а   — вещественная или комплексная функция на некотором многообразии.

В трёхмерной декартовой системе координат уравнение принимает форму:

При Адиабатическом расширении газа его температура понижается, а при сжатии – повышается. (Закон Пуассона)

Вывод уравнения

Согласно закону Менделеева — Клапейрона^[6] справедливо соотношение

где R — универсальная газовая постоянная. Продифференцировав обе части, получаем

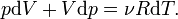
(3)

Если в (3) подставить   из (2), а затем   из (1), получим или, введя коэффициент  :

. Это уравнение можно переписать в виде что после интегрирования даёт уравнение . Окончательно получаем что и требовалось доказать.

• Поясним понятие работы применительно к адиабатическому процессу. В частном случае, когда работа совершается через изменение объёма, можно определить её следующим способом: пусть газ заключён в цилиндрический сосуд, плотно закрытый легко скользящим поршнем, если газ будет расширяться, то он будет перемещать поршень и при перемещении на отрезок 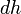  совершать работу^[9][10] 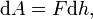где F — сила, с которой газ действует на поршень. Перепишем уравнение:

где s — площадь поршня. Тогда работа будет равна^[9][10]

где   — давление газа,   — малое приращение объёма. Аналогично видно, что уравнение выполняется и для сосудов с произвольной поперечной формой сечения. Данное уравнение справедливо и при расширении на произвольных объёмах. Для этого достаточно разбить поверхность расширения на элементарные участки   на которых расширение одинаково^[9].

Основное уравнение термодинамики примет вид^[11]:

(1)

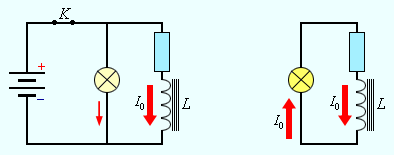
3. Ток, возбужденный магнитным полем в замкнутом контуре, называется индукционным, а само явление возбуждения тока посредством магнитного поля – электромагнитной индукцией. Электродвижущая сила, обусловливающая индукционный ток, называется электродвижущей силой индукции.

Рассмотрим несколько опытов, с помощью которых Фарадей изучал явление электромагнитной индукции (рис. 113).

1. К замкнутому контуру (плоскость которого перпендикулярна плоскости рисунка) приближается северный полюс магнита (рис. 113, а) . При этом в контуре индуцируется ток / ь вызывающий отклонение стрелки гальванометра Г. Магнитные поля магнита и индукционного тока изображены линиями индукции В и В Если движение магнита прекращается, то индукционный ток исчезает.

2. Северный полюс магнита удаляется от контура (рис. 113, б). Тогда в контуре индуцируется ток, противоположный току, индуцированному в предыдущем случае.

3. К контуру приближается южный полюс магнита (рис. 113, в). В этом случае индуцированный ток имеет такое же направление, как в случае удаления северного полюса магнита.

4. Южный полюс магнита удаляется от контура (рис. 113, г). Тогда индуцированный ток направлен так же, как в случае приближения северного полюса магнита.

5. В контуре включается ток / (ключом К) или же в этом контуре увеличивается сила (реостатом R) имеющегося уже тока (рис. 113, д).

Тогда в соседнем контуре индуцируется ток / г, направленный проти- ноположно току 1. Если изменение силы тока I прекращается, то ин-дукционный ток исчезает.

6. В контуре выключается или же уменьшается сила тока / (рис. 113, е). Тогда в соседнем контуре индуцируется ток /г, направленный одинаково с током I. Характерная особенность рассмотренных случаев состоит в том, что в каждом из них имеет место изменение потока магнитной индукции сквозь площадь, ограниченную контуром. Действительно, в случаях а, в, д этот поток увеличивается со временем, а в случаях б, г, е — уменьшается со временем. Обобщая результаты своих многочисленных опытов по электро-магнитной индукции, Фарадей пришел к следующим выводам. В замкнутом контуре индуцируется ток во всех случаях, когда происходит изменение потока магнитной индукции сквозь площадь, ограниченную контуром. Электродвижущая сила индукции пропорциональна скорости изменения потока магнитной индукции [закон Фарадея]: Эпсилон =(прибл) df/dt

Индукционный ток имеет такое направление, что его собственное магнитное поле компенсирует изменение потока магнитной индукции, вызывающее этот ток [правило Ленца]. Иными словами, индукционный ток направлен так, что его собственное магнитное поле препятствует изменению потока магнитной индукции, вызвавшему этот ток.

Потокосцепле́ние (полный магнитный поток) — физическая величина, представляющая собой суммарный магнитный поток, сцепляющийся со всеми витками катушки индуктивности.

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

где   — поток магнитного поля через замкнутую поверхность  , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре.

Вихревое поле – это поле, дивергенция которого равна нулю. То есть, говоря по-простому, это поле не имеет источников, а значит его силовые линии замкнуты. Такое поле может быть задано векторным потенциалом.

Примером вихревого поля является магнитное поле. Источником магнитного поля является электрический ток. Силовые линии магнитного поля прямолинейного тока представляют собой окружности, центром которых является проводник с током.

№12

1. Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.Кинетическая энергия — часть полной энергии, обусловленная движением.

Потенциальной энергией называют энергию взаимодействия тел или частей тела, зависящую от их взаимного положения.

Потенциальная энергия упруго деформированного тела — физическая величина, равная половине произведения жесткости тела на квадрат его деформации.

также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к не растянутому состоянию, то есть найдем упругую энергию растянутой пружины.

Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.

Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, то есть чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы.

2. Для реальных газов необходимо учитывать размеры мо­лекул и их взаимодействие друг с другом. Учитывая собственный объем молекул и сил межмолекулярного взаимодействия, физик И. Ван-дер-Ваальса вывел уравнения состояния реального газа. Наличие сил отталкивания, которые про­тиводействуют проникновению в занятый молекулой объем других молекул, сводит­ся к тому, что фактический свободный объем, в котором могут двигаться молеку­лы реального газа, будет не V_m, a V_m -b, где b — объем, занимаемый самими молекулами. Объем b равен учетверенному соб­ственному объему молекул. Действие сил притяжения газа приводит к появле­нию дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса, внутрен­нее давление обратно пропорционально квадрату молярного объема, т. е. P(внутр) = a/V²_m, где а— постоянная В-д-В, ха­рактеризующая силы межмолекулярного притяжения, V_m — молярный объем.

Для произвольного количества вещества v газа (v=т/М) с учетом того, что V = vV_m, уравнение Ван-дер-Ваальса примет вид ( .

Кривые зависимости р от V_m при заданных Т, определяемые уравнением Ван-дер-Ваальса (61.2) для моля газа: При некоторой температуре Т_к на изотерме имеется лишь одна точка перегиба К. Эта изотерма называется кри­тической, соответствующая ей температу­ра T_к — критической температурой. Кри­тическая изотерма имеет лишь одну точку перегиба К, называемую критической точ­кой; в этой точке касательная к ней па­раллельна оси абсцисс. Соответствующие этой точке объем V_к и давление р_к на­зываются также критическими. А само состояние называется критическим состоянием. При низких температурах (Т<Т_к) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.

3.Теория Максвелла. Переменные эл-е и магнитные поля не могут сущ-ть по отдельности: изменяющееся магнит.поле порождает электрическое поле,и наоборот.

Энергия магнитного поля, создаваемого током в замкнутом контуре индуктивностью L, равна где I — сила тока в контуре.Энергия магнитного поля катушки с индуктивностью L, создаваемого током I, равна