2. Основы научно-теоретических знаний по модулю

2.1. Вязкость жидкости. Формула Ньютона

Любая реальная жидкость и газ обладают свойством вязкости. Вязкость является одной из причин, вызывающей сопротивление течению жидкости по трубам и каналам (внутренняя задача гидромеханики) и движению твердого тела в жидкости (внешняя задача гидромеханики).

Между слоями в потоке вязкой жидкости действуют силы, касательные к направлению их движения. При этом слои жидкости, расположенные ближе к стенке, подтормаживают верхние слои, что приводит к характерному виду эпюры скорости, изображенной на рис. 1.1.

Рис. 1.1. К понятию вязкости жидкости

Юшкин, стр. 13

Прандтль, стр. 142

Силы трения, возникающие между движущимися друг относительно друга слоями жидкости с площадью соприкосновения dS (рис. 1.1), можно определить на основании формулы Ньютона:

(1.1)

или, если отнести силу трения к площадке dS и обозначить получаемое при этом касательное напряжение через ,

. (1.2)

В этой формуле – производная, характеризующая изменение скорости в поперечном к слою направлении, которая согласно рис. 1.1 , 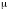– динамический коэффициент вязкости, зависящий от свойств жидкости. Формула (1.2), предложенная Ньютоном вначале в качестве гипотезы и подвергавшаяся в дальнейшем тщательной опытной проверке, в настоящее время общепринята в гидромеханике для расчета касательных напряжений при ламинарном течении жидкостей и именуется формулой ньютона (законом внутреннего трения Ньютона).

Ламинарным, то есть слоистым, называется течение вязкой жидкости, при котором отсутствует перемешивание между ее слоями. Неупорядоченное движение вязкой жидкости с интенсивным перемешиванием частиц называется турбулентным. В случае турбулентного течения формула Ньютона неприменима.

Динамический коэффициент вязкости  зависит от рода жидкости, ее температуры и (в малой степени) от давления. Размерность  согласно (1.2) [μ] = ML^–1T^–1.

В системе единиц СИ размерность [] = Н сек м^-2, а в технической []= кГ сек м^-2.

Широкое применение в гидромеханике находит также кинематический коэффициент вязкости , представляющий отношение  к плотности жидкости .

.

Размерность [ μ] = L²T^–1, откуда следует, что в коэффициент не входят динамические характеристики.

На рис. 1.2 показаны зависимости кинематического коэффициента  в функции от температуры – для воды и в функции от температуры и давления – для воздуха. Как видно из рисунка, для воды этот коэффициент примерно на порядок меньше, чем для воздуха. Это означает, что вода относительно менее вязкая жидкость, нежели воздух. Коэффициенты вязкости  и  определяются опытным путем.

Выясним физическую причину возникновения вязкости на примере газа; для этого необходимо учесть его молекулярное строение. Молекулы движущегося газа совершают хаотическое тепловое движение, перескакивая из слоя в слой. При этом происходит обмен количеством движения между слоями.

Между слоями, согласно закону изменения количества движения, возникают силы, которые имеют характер сил сопротивления (трения). Этот обмен количествами движения совершается на «молекулярном уровне». Таким образом, вязкость обусловливается наличием молекулярного движения газа.

Вводя коэффициент вязкости , как физическую характеристику жидкости и тем самым косвенно учитывая действие этого молекулярного движения в газе, можно в дальнейшем по-прежнему использовать гипотезу сплошности для вязкой жидкости, не прибегая к прямому учету молекулярных взаимодействий.

Касательное напряжение равно нулю, если μ = 0, то есть если жидкость лишена свойств вязкости. Второй фактор, определяющий наличие касательных напряжений в жидкости, связан с существованием изменения скорости по нормали (градиент скорости). Если , то τ = 0 даже в вязкой жидкости.

Жидкости, подчиняющиеся закону внутреннего трения Ньютона, называются нормальными, или ньютоновскими. К ним относятся наиболее важные жидкости и газы, такие, как вода, воздух, нефтепродукты, ртуть и др.

Жидкости, в которых связь между напряжениями и градиентами скоростей не подчиняется формуле (1.2), называются аномальными, или неньютоновскими. К ним относятся некоторые смазочные масла при низких температурах, коллоидные растворы, масляные краски, глинистые растворы, а также растворы в воде некоторых высокомолекулярных соединений. Движение подобных аномальных жидкостей исследуется в реологии, а также в специальных разделах гидромеханики.