1.Структура механизмов. Звено. Кинематическая пара.
Под структурой механизма понимается совокупность его элементов и отношений между ними, т.е. совокупность звеньев, групп или типовых механизмов и подвижных или неподвижных соединений. Структурная схема-графическое изображение механизма, выполненное с использованием условных обозначений, рекомендованных ГОСТ или принятых в спец.литературе, содержащее информацию о числе и расположении элементов, а также о виде и классе кинематических пар, соединяющих эти элементы. Структурная схема не содержит информации о размерах звеньев и вычерчивается без соблюдения масштабов. Звено- деталь или группа взаимнонеподвижных деталей, которые совершают определенные вынужденные движения. Кинематическая пара-подвижное соединение 2-х звеньев.
2. Классификация кинематических пар.
Любая кинематическая пара накладывает ограничения на движение входящих в нее звеньев, эти ограничения называются условиями связи (S). Класс кинематической пары определяется числом условий связи. S=6-H; H(число степеней свободы)=6-S; 1≤S≤5
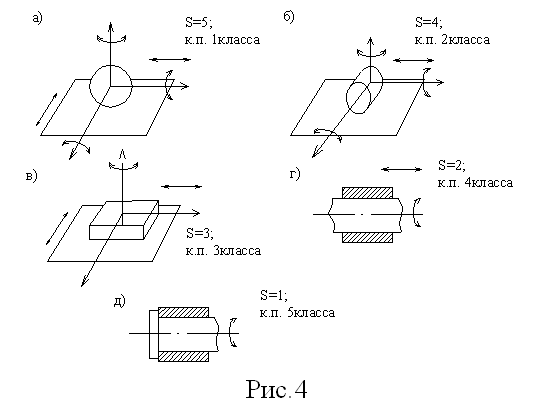
Точки, линии, пов-ти по которым звенья соприкасаются в кин.паре наз-ся элементами кин.пары.
Если элементами кин.пары яв-ся точка или линия она называется высшей.
Если элементами яв-ся пов-ти, они называются низшими.
3.Кинематическая цепь. Классификация кинематических цепей.
Система звеньев, связанных между собой кинематическими парами наз-ся кинематической цепью.
Для кинематической цепи общего вида пространственных механизмов структурная формула (формула Сомова-Малышева):W=6·n-5·p5-4·p4-3· -2·p2-p1
Для плоских механизмов (формула Чебышева): W=3·n-2м·p5-p4
n-число подвижных звеньев в кинематической цепи механизма;
p5, p4, p3, p2, p1- число кинематических пар соответственно 5,4,3,2 и 1 классов по классификации Артоболевского. Кинематические цепи делятся на простые и сложные. Простой кин.цепью наз-ся такая цепь, у которой каждое звено входит не более чем в две кин.пары.
Сложной кин.цепью наз-ся цепь, в которой имеется хотя бы одно звено, входящее более чем в две кин.пары.
Простые и сложные кин.цепи делятся на замкнутые и незамкнутые. Замкнутой кин.цепью наз-ся кин.цепь, каждое звено которой входит по крайней мере в две кинематические пары. Незамкнутой кин.цепью наз-ся кин.цепь, в которой есть звенья, входящие только в одну кин.пару.
4.Степень подвижности пространственных и плоских механизмов.
Для кинематической цепи общего вида пространственных механизмов структурная формула (формула Сомова-Малышева):W=6·n-5·p5-4·p4-3· -2·p2-p1
Для плоских механизмов (формула Чебышева): W=3·n-2м·p5-p4
n-число подвижных звеньев в кинематической цепи механизма;
p5, p4, p3, p2, p1- число кинематических пар соответственно 5,4,3,2 и 1 классов по классификации Артоболевского.
Плоским наз-ся механизм, точки звеньев которого описывают траектории в одной или параллельных плоскостях.
5. Пассивные условия связей и лишние степени свободы.
Пассивными условиями связи и лишними степенями подвижности наз-ся такие условия связи и степени подвижности, которые не влияют на характер движения звеньев механизма.
Удаление из механизмов звеньев и кинематических пар, которым эти степени свободы и условия связи принадлежат, может быть сделано без изменения общего характера движения механизма в целом.