7. Анализ устойчивости сау. Критерии устойчивоси

Устойчивость — способность системы возвращаться в исходное состояние после прекращения действия возмущения.

Математическое условие устойчивости может быть определено из ДУ. Если корни уравнения вещественные: … …

Система устойчива, если корни характеристического уравнения отрицательны. Если корни комплексносопряженные то система устойчива, если ai<0, амплитуда синусоиды экспоненциально уменьшается.

Для определения используют критерий устойчивости: алгебраический Гурвица, частотный Найквиста.

Критерий Гурвица основан на составлении определителя из коэффициентов характеристического уравнения.

Достоинство — позволяет достаточно просто определить устойчивость систем любого порядка.

Недостатки — не позволяет определить насколько близко к границе устойчивости находится система.

Критерий Найквиста

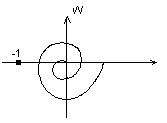Линия образована очерчиванием колец вектора модуль которого , а угол этого вектора — сдвиг фаз между входным и выходным сигналом.

Впервые был предложен для определения устойчивости…..

В соответсивии с критерием Найквиста система будет устойчива, если АФХ соответствующей ей разомкнутой системы не лхватывает точку с координатой (-1;0).

Поеимущество — позволяет определить насколько близко к границе устойчивости находится система.

Практическая пригодность систем регулирования определяется их устойчивостью и приемлемым качеством регулирования. Под устойчивостью понимают способность системы возвращаться в исходное состояние при прекращении возмущающего воздействия. Система может быть устойчива при воздействиях любой величины (устойчивость в большом) или при некоторых ограниченных воздействиях (устойчивость в малом).

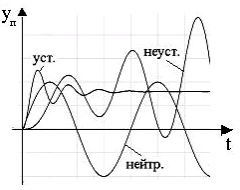
Анализ системы на устойчивость основан на решении однородного дифференциального уравнения, описывающего свободное движение: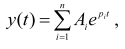

Условием устойчивости является:

Если корни характеристического уравнения вещественные и разные, то выходная величина будет монотонно изменяться, а характер изменения каждой составляющей будет определяться знаком соответствующего корня.

Если p_i = 0, то i–я составляющая принимает постоянное во времени состояние. При p_i > 0 соответствующая ему составляющая будет с течением времени увеличиваться до бесконечности. Следовательно, система будет устойчива только в том случае, если все корни характеристического уравнения меньше нуля.

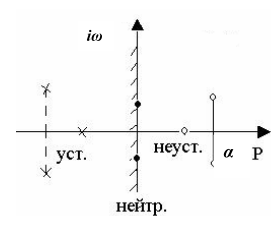
Если корни характеристического уравнения сопряженные комплексные (p_i = α_i ± jω_i), то составляющие переходного процесса будут иметь колебательный характер:

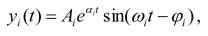
где А_i и φ_i – постоянные интегрирования.

В этом случае система будет устойчива, если все вещественные части корней (α_i) будут отрицательными, а амплитуда колебаний будет стремиться со временем к нулю.

Корни характеристического уравнения легко определяются, если его степень не выше второй. Решение уравнений более высоких порядков связано с большими трудностями и выполняется с использованием численных методов. Поэтому были разработаны методы, позволяющие исследовать системы на устойчивость с помощью специальных критериев, не вычисляя при этом корней характеристического уравнения. Одним из таких критериев является алгебраический критерий Гурвица, который формулирует условие устойчивости в виде определителей.

Для этого из коэффициентов характеристического уравнения составляют определитель. По главной диагонали выписывают последовательно все коэффициенты характеристического уравнения, начиная с а₁ . Затем заполняют столбцы коэффициентами: вверх от главной диагонали – по возрастанию индексов до а_n , вниз – по убыванию до а 0 . Оставшиеся пустыми места заполняют нулями. Затем из матрицы выделяют диагональные определители, удаляя последовательно равное количество строк и столбцов.

По алгебраическому критерию система n–порядка устойчива, если a₁ , а также все диагональные определители больше нуля.

Критерий Гурвица позволяет только установить факт устойчивости, и по полученным значениям невозможно определить, насколько близко к границе устойчивости находится система.

Критерий Найквиста (амплитудно-фазовый) был предложен для исследования устойчивости усилителей с обратной связью. Он позволяет судить об устойчивости замкнутой системы по поведению соответствующей ей разомкнутой системы, что упрощает расчеты.

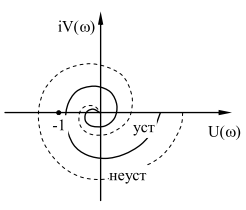
Замкнутая система устойчива, если АФХ соответствующей ей разомкнутой системы W(jω ) при изменении частоты от 0 до бесконечности не охватывает точки с координатами -1, i0.

Достоинством критерия Найквиста является возможность оценить, как близко к границе устойчивости находится система.