4. Методы математического описания сау. Передаточная функция

Поведение АСР в процессе функционирования представляет собой сочетание статических и динамических режимов. Для синтеза АСР и еѐ отдельных элементов, а также исследования их характеристик необходимо иметь уравнения, связывающие входные и выходные параметры. Различают статическую и динамическую модели (характеристики).

Статические характеристики АСР.

Статическая модель описывает поведение системы в равновесном состоянии: , где у – выходная величина, х – входная величина.

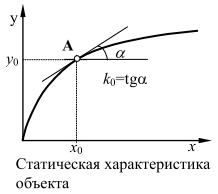
В общем случае функция (*) нелинейна, поэтому ее линеаризуют, раскладывая в ряд Тейлора в окрестностях рабочей точки:

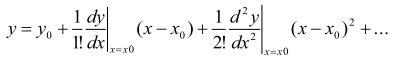
Оставляя только линейные члены ряда можно записать:

где - коэффициент передачи объекта.

Если выходная величина объекта зависит от нескольких входных воздействий, то при линеаризации по методу малых приращений следует определять частные производные по всем воздействиям, а приращение выходной величины является суммой частных приращений входных воздействий, т.е:

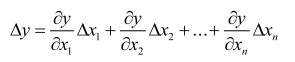
где Δx₁ , Δx₂ , …, Δx_n – приращения входных воздействий.

Динамические характеристики.

Динамические характеристики элементов АСР описываются 2-мя способами: 1) Дифференциальные уравнения 2) Передаточные функции (последовательное соединение звеньев, параллельное соединение звеньев, замкнутая обратная связь)

Динамическая модель описывает изменение входных и выходных величин во времени. Если объект имеет один выход, то динамическая модель в общем случае имеет вид:

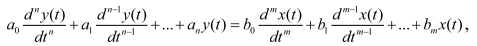
где y(t), x(t) – выходная и входная величины; a_i и b_i , – постоянные коэффициенты; n – порядок уравнения, при этом n ≥ m – условие физической реализуемости элемента.

Если входных величин несколько – то они и их производные записываются в правой части уравнения.

Если объект имеет k выходов, то его динамика описывается системой k дифуравнений.

Динамические характеристики рассматривают при трех стандартных

входных воздействиях:

- единичном ступенчатом – 1(t),

- единичном импульсном – δ(t),

- периодическом (синусоидальном).

В первых двух случаях полученные характеристики называются временными, в третьем – частотными. По временным характеристикам определяют качество регулирования.

Уравнения динамики решаются классическим или операторным методами. Классический метод применяют для решения линейных уравнений, если их порядок не превышает трех, а правая часть выражается простой функцией – константой или синусоидой. В этом случае общее решение уравнения динамики (неоднородное дифуравнение) представляет собой сумму общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение характеризует поведение системы, предоставленной самой себе, после снятия внешних возмущений. Его называют уравнением свободного движения системы:

.

Частное решение неоднородного уравнения описывает поведение системы, определяемое свойствами системы и видом воздействия, и называется вынужденным.

Тогда: .

Решением уравнения свободного движения является:

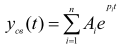где p_i – корни характеристического уравнения:

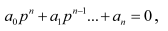
A_i – постоянные интегрирования, определяемые из начальных условий.

Операторный метод решения уравнений динамики предусматривает:

- приведение дифуравнений к операторной форме, применяя преобразование Лапласа с учетом заданных начальных условий;

- решение полученного алгебраического уравнения относительно искомой величины, записанной в операторной форме, используя в случае необходимости свойства преобразования;

- нахождение решения исходного уравнения динамики в обычной форме, применяя операцию обратного преобразования Лапласа.

Прямым преобразованием Лапласа функции f(t) действительного переменного t называется функция F(p) комплексного аргумента p = α + iω определяемая по формуле:

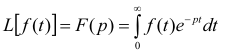
где L – символ операции прямого преобразования Лапласа.

Функцию f(t), называют оригиналом, а функцию F(p),– изображением.

Уравнение динамики системы в операторной форме всегда проще исходного дифференциального уравнения. При этом оно учитывает начальные условия и отражает физическую картину переходного процесса в системе.

Для отыскания оригинала по соответствующему изображению F(p) необходимо провести операцию обратного преобразования Лапласа, которая обозначается символом L^-1:

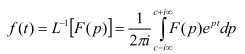
Вычисление интеграла затруднительно и поэтому решения для распространенных случаев приводятся в таблице.

Если изображения нет в таблице, то его необходимо привести к удобной для решения форме. Часто изображение F(p) можно выразить в виде дробно-рациональной функции от р:

.

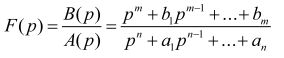если один из корней знаменателя равен 0, то оригинал может быть найден по формуле:

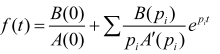, где р_i – ненулевые корни знаменателя.

Выраженное в операторной форме уравнение динамики позволяет найти передаточную функцию системы:

.

где Y(p) и X(p) – изображения по Лапласу выходной и входной величин при нулевых начальных условиях соответственно.

С помощью передаточных функций можно упростить описание динамики как АСР в целом, так и их элементов.

Передаточная функция АСР состоящая из n параллельно соединенных звеньев равна сумме передаточных функций отдельных ее звеньев.