22. Алгоритм математического моделирования объектов управления (резервуар с жидкостью)

Составление математического описания объектов начинают с нахождения уравнений его материального или энергетического балансов за бесконечно малый промежуток времени dt, выявления кинетических закономерностей, гидродинамических условий и т.п. Нелинейные дифференциальные уравнения линеаризуют.

Далее от абсолютных значений входных и выходных величин переходят к их приращениям. Последние, в свою очередь, заменяют безразмерными величинами, которые представляют собой отношения абсолютных приращений этих величин к их произвольно выбранным базисным значениям. В качестве таковых обычно используют значения величин в равновесном состоянии до нанесения возмущающего воздействия.

Полученные уравнения приводят к общепринятой форме путем группирования в левой части всех членов, содержащих выходную величину объекта и ее производные, а в правой части – всех членов, содержащих входную величину объекта и ее производные.

Резервуар c жидкостью.

Пусть вода подается в резервуар с расходом Gп и откачивается из него насосом с производительностью Gр. Входными величинами являются Gп и Gр, а выходная величина – уровень в емкости.

В равновесном состоянии: Gр0= Gп0= G 0

и уровень не изменяется. Неравенство входного и выходного потоков приведет к изменению объема воды в резервуаре: 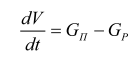, если площадь

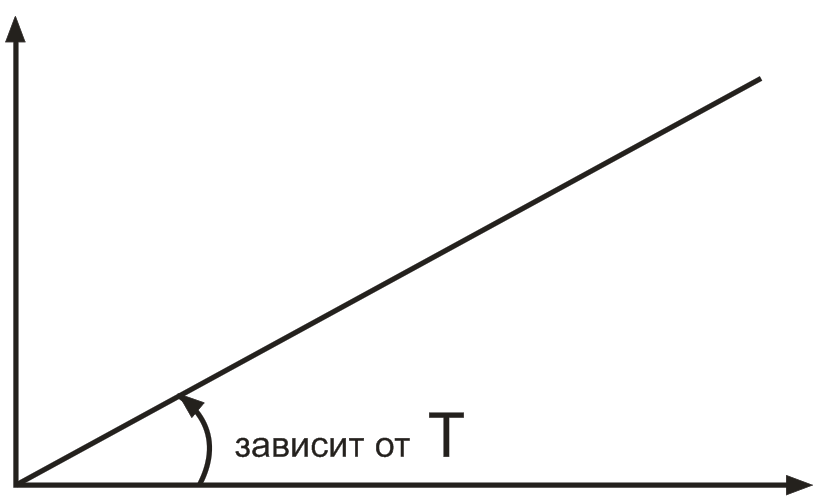
сечения емкости постоянна (V = SH), то: .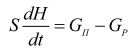

Уравнение математического баланса:

Gn = Gp

H = f(t)

Gn – Gp = dV/dt

Резервуар имеет постоянное сечение по H:

V = S * H

S * dH/dt = Gn – Gp

От абсолютных значений переходят к приращениям:

H = Ho + ∆H

Gn = Gno + ∆Gn

Gp = Gpo + ∆Gp

Gno = Gpo

S * d(∆H)/dt = Gno + ∆Gn + (–Gno – ∆Gp) = ∆Gn – ∆Gp = ∆G

Переходим к безразмерным величинам, все величины делим на базисные величины:

Y = ∆H/Ho X = ∆G/Go Go = Gno = Gpo

S * d(YHo)/dt = X * Go

SHo/Go * dY/dt = X, SHo/Go = T =› T * dy/dt = X – интегрирующее звено

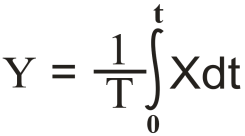
dY/dt = C – емкость (площадь сечения резервуара)

23. Классификация измерений.

Измерение – экспериментальное нахождение размера физической величины с помощью специального технического средства (средства измерения).

По изменению во времени:

- статические (измеряемая величина остаётся постоянной во времени в процессе измерения)

- динамические (измеряемая величина изменяется в процессе измерения)

По числу наблюдений:

- однократные (используются, если системные погрешности определяющие и больше случайных) высокие скорости

-многократные (используются в научных исследованиях, высокая точность, большая продолжительность)

По способу получения информации:

- прямые (искомое значение физической величины находят непосредственно из опыта) Массу меряют весами.

- косвенные (искомое значение находят на основании прямых измерений других физических величин функционально связанных с искомыми величинами) Измерение плотности по изменению массы и объёма.

По первому классификационному признаку измерения подраз­деляют на: статические, при которых измеряемая величина остает­ся постоянной во времени в процессе измерения, и динамические, при которых измеряемая величина изменяется в процессе измере­ния.

Классификация по второму признаку является в большой степе­ни условной, однако широко применяется в измерительной технике. Ею определяются сложившиеся совокупности родственных по при­роде или применению в отдельных областях науки или техники фи­зических величин.

По третьему признаку измерения подразделяют на три класса.

Измерения максимально возможной точности, достижимой при современном уровне техники. Это измерения, связанные с создани­ем и воспроизведением эталонов, а также измерения универсальных физических констант.

Контрольно-поверочные измерения, погрешности которых не должны превышать заданного значения. Такие измерения осу­ществляются в основном государственными и ведомственными мет­рологическими службами.

Технические измерения, в которых погрешность результата опре­деляется характеристиками средств измерений. Технические изме­рения являются наиболее распространенными и выполняются во всех отраслях хозяйства и науки. К ним, в частности, относятся и технологические измерения.

Четвертым классификационным признаком служит число изме­рений (наблюдений при измерении или просто наблюдений), выполняемых для получения результата. Здесь различают измерения с однократным наблюдением (обыкновенные) и измерения с много­кратными наблюдениями (статистические).

Прямыми называют измерения, при которых искомое значение величины находят непосредственно из опытных данных. В процессе прямого измерения объект измерения приводится во взаимодей­ствие со средством измерений и по показаниям последнего отсчи­тывают значение измеряемой величины или указанные показания умножаются на постоянный коэффициент для определения значе­ния измеряемой величины. Примером прямых измерений могут служить: измерение длины линейкой, массы с помощью весов, тем­пературы стеклянным термометром и т. д. К прямым измерениям относят измерения подавляющего большинства параметров химико-технологических процессов.

Косвенными называют измерения, при которых искомое значе­ние величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. При косвенных измерениях путем прямых измерений находят зна­чения величин-аргументов, а значение измеряемой величины Y определяют путем вычисления по формуле Y=f (X₁, X₂, … , X_m), где X₁, X₂, … , X_m — величины-аргументы.

Совокупными называют производимые одновременно измерения нескольких одноименных величин, при которых искомые значения величины находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин или ряда других величин, функционально связанных с измеряемыми.

Совместными называют проводимые одновременно измерения двух или нескольких неодноименных величин для нахождения за­висимости между ними.