9.Способы замены граничных условий сеточными уравнениями.

Будем рассматривать задачу Дирихле на основе уравнения Лапласса в области D c замкнутым контуром Г 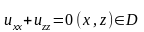(1)

Требуется найти функцию u(x,z), которая в области D удовлетворяет уравнению (1), а на контуре Г этой области следующему граничному условию 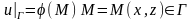(2)

 - функция известная, а М – точка, принадлежащая замкнутому контуру Г.

Будем считать, что выбрана прямоугольная сетка, построена сеточная область D_h, заменяющая область D. В этой области D_h выделим множество внутренних узлов и множество граничных узлов. Задача состоит в том, чтобы граничное условие (2) заменить некоторым сеточным условием. Для решения этой задачи большое значение имеет геометрическая картина. Если область D является прямоугольником, то сетка строится т.о., чтобы граничные узлы лежали непосредственно на границе Г. Если же область имеет криволинейную границу Г, то к внутренним узлам отнесем всякий, для которого 4 соседних узла лежат внутри области D_h, другие узлы будем считать граничными. На рисунке граничные узлы обозначены *, а внутренние – о. Следует различать граничные точки и граничные узлы.

Н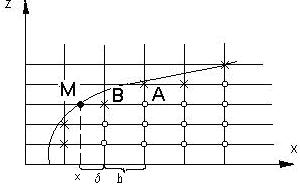 а рисунке обозначены М- граничная точка, (точка, лежащая на границе Г), В – граничный узел, А – внутренний узел. Необходимо определить, каким следует взять сеточное значение функции в точке В.

Простейшим решением этой задачи является след. взять в качестве значения u(В) значение функции  в точке контура, ближайшей к точке В, т.е. полагают u(В)= (М). Такой способ замены граничных условий получил название простого сноса граничных условий в ближайшую точку сетки. Погрешность этого способа имеет первый порядок О(h).

Чтобы уменьшить погрешность аппроксимации граничных условий, целесообразно использовать метод, который называется метод линейного интерполирования и дает погрешность второго порядка О(h²). В этом случае для вычисления значения функции в граничном узле u(В) нужно использовать значение фу-ии в граничной точке М(x,z) , а также значение этой функции в некоторой внутренней точке А(x+h,z), ближайшей к граничному узлу В. Здесь  - расстояние между граничной точкой М и ближайшим граничным узлом В (эта величина берется со знаком “+”, если узел В расположен внутри области и со знаком “-”, если узел В лежит вне области D; h – шаг сетки. Искомая формула получается из разложения u(В) и u(А) в окрестности точки М в ряд Тейлора. Окончательно приближенное значение сеточной функции в узле В можно вычислить по формуле 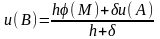(3)

Выражение (3) называют формулой Коллатца. В правой части этой формулы есть неизвестное слагаемое u(A), которое не позволяет сразу вычислить значение функции в граничном узле u(В), однако погрешность такой замены выше по сравнению со случаем непосредственного сноса граничных условий и имеет второй порядок О(h²).

По ходу решения задачи граничные условия, определенные формулой (3), можно уточнить, используя процесс Либмана.

10. Методы решения разностной задачи Дирихле

Пусть для задачи Дирихле (1),(2) 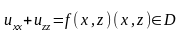(1)

(2)

методом сеток получена конечно-разностная схема

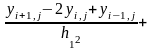
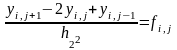(3)

i=1,2,…,N1-1 j=1,2,…,N2-1

y_i,0=(x_i,0) y_i,N2= (x_i,L2) i=0,..,N1

y_0,j=( 0, z_j) y_N1,j= (L1,z_j) j=0,..,N2 (4)

где L1 и L2 – максимальные значения области D по направлениям X и Z. Эта разностная схема (3)-(4) представляет СЛАУ относительно неизвестных значений сеточной функции y_i,j, состоящую из (N1-1)·(N2-1) уравнений с таким же количеством неизвестных.  Решение систем такого высокого порядка методом Гаусса (даже если N1,N2 не превышает 100, то число уравнений в системе будет порядка 10³-10⁴) требует почти (N1-1)³(N2-1)³, т.е. 10⁹-10¹² арифметических действий. Однако матрица системы (3)-(4) является слабо заполненной и имеет примерно 5N1*N2 ненулевых элементов. Поэтому для решения системы разностных уравнений (3)-(4) можно построить методы, с гораздо меньшим количеством действий, вплоть до (N1-1)(N2-1). В основе построения таких методов лежит метод разделения переменных, который комбинируют либо с методом редукции, либо с алгоритмом быстрого преобразования Фурье. Такие методы являются наиболее экономичными для области прямоугольной формы. Однако, если переменные не разделяются, или область не является прямоугольником , а также если в основе задачи лежит уравнение с переменными коэффициентами, то для решения системы (3)-(4) используют итерационные методы. В этом случае каждое из уравнений системы необходимо записать в виде, разрешенном относительно сеточной функции в центральном узле

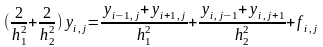(5)

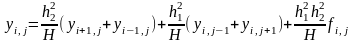Или (6)

Где .

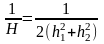Если сетка является квадратной, то получаем уже известное выражение

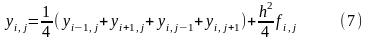Всякий итерационный процесс предусматривает выбор начального приближения и контроль максимального отклонения значений сеточной функции для двух последовательных итераций в соответствующих узлах ., k- номер итерации. Если величина этого отклонения M≤ достигает заданной точности, итерационный процесс прекращается, и значение функции на последней итерации принимается за искомое решение.

Одним из способов решения задачи Дирихле является сведение ее к решению некоторой фиктивной нестационарной задачи, т.к. при достаточно больших значениях параметра времени t решения нестационарной и аналогичной стационарной задачи достаточно близки. Такой способ решения называется методом установления.

Решение u(x,z) задачи (1)-(2) не зависит от времени, поэтому можно добавить в уравнение (1) слагаемое, которое равно нулю при точном решении. В этом случае уравнение (1) можно записать следующим образом 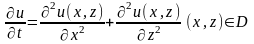(8)

Уравнение (8) представляет собой двумерное нестационарное уравнение теплопроводности, для которого известно множество способов построения разностных схем. Необходимо только для разрешимости задачи в такой постановке к краевым условиям (2) добавить начальное условие. Это условие можно принимать практически в произвольном виде, согласовав его с граничными условиями. Пусть начальное условие задается следующим образом 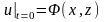(9)

Граничное условие (2) задачи Дирихле при этом остается стационарным, т.е. не зависящим от времени. (10)

Процесс числен. решения задачи Дирихле в постановке (8)-(10) состоит в переходе при t от произвольного значения функции u, которое мы берем из условия (9) к искомому стационарному решению. Счет ведется до выхода на стационар. режим, т.е. ограничиваются решением при некотором достаточно большом значении t, если значения искомой функции u на 2х соседних итерациях совпадают с заданной степенью точности.

Метод установления является итерационным процессом решения задачи Дирихле в постановке (8)-(10). Причем на каждой итерации значение искомой функции u(x,z) получаются путем численного решения некоторой вспомогательной нестационарной задачи. В теории разностных схем доказывается, что такой итерационный процесс является сходящимся к решению исходной стационарной задачи, если решение стационарной задачи существует.

МathСad имеет две функции для решения задачи Дирихле в области с квадратной матрицей. Если на всех четырех сторонах квадрата заданы граничные ненулевые условия, то используется функция relax. Эта функция возвращает квадратную матрицу, в которой

• индекс элемента матрицы совпадает с нумерацией узлов квадратной сетки

• значение элемента матрицы является аппроксимацией искомого реш. в этой точке.

Функция relax имеет следующие аргументы

Relax(a,b,c,d,e,f,u,w)

a,b,c,d,e, - квадратные матрицы, содержащие коэффициенты исходного уравнения Пуассона. f- квадратная матрица значений правой части исходного уравнения, u – матрица начальных приближений для граничных и внутренних узлов области решения, w- параметр релаксации, имеет положительное значение не превышающее единицы.

Уравнение Пуассона вида

на квадратной сетке представляем следующим образом

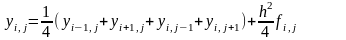
Параметры функции в этом случае имеют значение

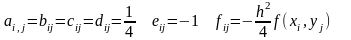
Если на всех сторонах квадрата мы имеем нулевые граничные условия, то можно использовать функцию multigrid.