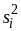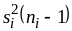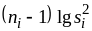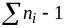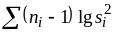25. Методика проверки гипотезы однородности ряда дисперсий при равном объеме выборок, взятых из нормальной генеральной совокупности. Как определяется расчетное и критическое значения критерия g?

Пусть имеется m выборок не равных объемов n_i, взятых из одной или m генеральных совокупностей, имеющих нормальные распределения. При этом дисперсии этих совокупностей имеют одинаковые значения, т. е. , а математические ожидания могут быть и не равны друг другу. Дисперсии выборок , , ,…, , вычисленные по формуле 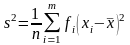, несколько отличаются друг от друга по величине. Требуется проверить гипотезу о том, что это различие дисперсий выборок носит случайный характер, и, следовательно, дисперсии генеральных совокупностей , из которых взяты выборки, равны между собой, т.е. . При нашей гипотезе величину , (11) где , следует считать несмещенной оценкой σ². Если проверяемая гипотеза справедлива, то случайная величина 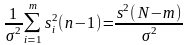будет иметь распределение χ² с (N - m) степенями свободы. Очевидно, что распределение отношения при нашей гипотезе зависит лишь от n_i. Бартлет показал, что случайная величина , (12) где 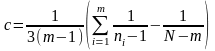имеет распределение, близкое к распределению χ² с (m - 1) = k степенями свободы, если только n_i ≥ 3. Для вычисления Q пользуются следующей формулой, в которой сделан переход от натуральных к десятичным логарифмам: 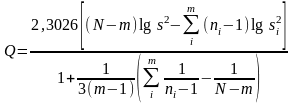. (13) Задаваясь доверительным уровнем вероятности, например, q = 0,05 и пользуясь табл. П.4 приложения, определяют верхний критический предел χ² при (m - 1) = k степеней свободы. Если q < χ², то гипотеза принимается, если q > χ², то гипотеза бракуется. Для вычисления Q рекомендуется составлять вспомогательную таблицу 3.

№ выборки

Таблица 3 Вспомогательная таблица для вычисления Q Если объемы выборок равны, т. е. n₁ = n₂ = …n_k = n, то формула (13) принимает вид 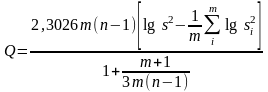, (14) где s² вычисляется по формуле . (15) Однако при равном объеме выборок проверку гипотезы однородности дисперсий проще производить упрощенным приемом³, основанным на вычислении критерия G: 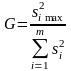. (16) Критические значения G для 5%-ного уровня значимости в зависимости от объема выборок n и числа выборок m приведены в табл. П.5 приложения. Если найденное по данным выборок G_н меньше табличного G (G_н < G), то гипотеза однородности дисперсий генеральных совокупностей, из которых были взяты выборки, принимается. Если G_н > G, то гипотеза бракуется.

27. Виды погрешностей обработки деталей, причины (источники) их возникновения. Характер изменения во времени функциональных погрешностей в зависимости от состояния и условий работы режущего инструмента.

Выделяют три вида погрешностей обработки деталей: погрешности размера, погрешности формы и погрешности взаимного расположения поверхностей и осей детали. При механической обработке деталей на металлорежущих станках источниками этих погрешностей являются станок, приспособление, инструмент и сама обрабатываемая деталь (сокращенно система СПИД).

В зависимости от причин, вызывающих погрешности обработки деталей, выделяют случайные погрешности и систематические. В свою очередь, систематические погрешности подразделяются на постоянные погрешности и закономерно изменяющиеся во времени, или функциональные. Таким образом, все погрешности механической обработки по причинам их образования классифицируют на три основных вида: постоянные, функциональные и случайные. Требуемая точность обработки в условиях серийного и массового производств обычно обеспечивается настроенным на размер станком. При работе на настроенных станках величина тех или иных погрешностей обработки практически не зависит от оператора, обслуживающего станок. Поэтому в этом случае можно дать следующие определения основным видам погрешностей обработки. Постоянными называются такие погрешности, которые сохраняют свое значение при обработке каждой новой детали. Функциональными называются такие погрешности, величина которых закономерно изменяется при обработке каждой новой детали. Случайными называются такие погрешности, величина которых при обработке каждой новой детали может принять любое численное значение (в определенных пределах), заранее нам неизвестное.

Постоянные погрешности обработки возникают вследствие неточности настройки режущего инструмента на размер, неточности изготовления станка, приспособления и мерного режущего инструмента. Погрешности в изготовлении станка, приспособления и режущего инструмента целиком переносятся и на обрабатываемую деталь. Поэтому в зависимости от вида обрабатываемой поверхности и изучаемого параметра точности обработки устанавливается и доминирующая причина постоянных погрешностей. Например, при обработке наружных и внутренних поверхностей резцом или фрезой доминирующей причиной постоянных погрешностей обработки будет неточность установки режущего инструмента на размер; при обработке мерным инструментом (разверткой, зенкером, протяжкой и т. п.) основной причиной постоянных погрешностей будет неточность изготовления режущего инструмента; при нарезании резьбы на токарно-винторезном станке основной причиной постоянной погрешности шага нарезаемой резьбы будет неточность шага ходового винта станка и т. д. Для погрешностей формы и взаимного расположения поверхностей основными причинами постоянных погрешностей будут являться геометрические неточности станка.

Функциональные погрешности. Главными причинами возникновения функциональных погрешностей обработки являются размерный износ режущего инструмента и его температурные деформации от нагрева в процессе резания, а также температурные деформации станка и температурные деформации обрабатываемой детали. Все эти погрешности являются функцией времени работы станка и режущего инструмента. Однако температурные деформации станка носят временный характер. По истечении определенного времени работы его температура стабилизируется и деформация частей станка прекращается, а погрешность, возникающая по этой причине, превращается в постоянную.

П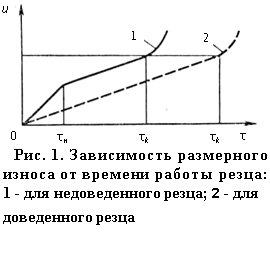 ри работе на настроенных станках или при работе мерным режущим инструментом размерный износ систематически изменяет размер каждой новой детали на удвоенную величину износа инструмента при выполнении диаметральных размеров или только на величину износа при выполнении размеров длин. Исследованиями установлено, что размерный износ u режущих инструментов протекает во времени τ по закону, выражаемому кривой 1, показанной на рис. 1. Эта кривая имеет три участка. Первый участок (от 0 до τ_н) характеризует изменение износа инструмента в период его приработки. Это участок начального износа инструмента. Второй участок (от τ_н до τ_к) характеризует нормальный износ инструмента и третий участок (от τ_к до конца кривой) - катастрофический износ, когда наступает быстрое разрушение инструмента.

Если работа производится предварительно доведенным инструментом, размерный износ будет изменяться во времени по закону прямой (см. рис. 1, линия 2). При этом период стойкости инструмента увеличится, так как доводка инструмента повышает его износостойкость в 1,5 и более раз. Размерный износ режущего инструмента и интенсивность износа зависят от материала режущего инструмента и материала обрабатываемой детали, от режима резания и геометрии инструмента. Характеристикой интенсивности размерного износа является относительный (удельный) износ u₀, т. е. износ в микрометрах, отнесенный к 1000м пути резания l: 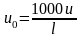. Путь резания l определяется по формуле 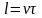, где v - скорость резания в м/мин;  - время работы режущего инструмента. Если известен относительный износ режущего инструмента, погрешность обработки , вызванная его размерным износом, может быть определена по следующим формулам:

а) для диаметральных размеров 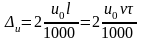мкм;(1) б) для размеров длин мкм.(2)

Этот вид погрешностей обычно определяется опытным путем для данных конкретных условий. Вместе с износом режущего инструмента одновременно происходит и деформация его от нагрева в процессе резания.

Исследованиями установлено, что температурные деформации режущего инструмента l в зависимости от времени  его работы протекают по закону, показанному на рис. 2. 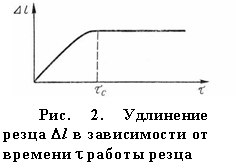До некоторого момента времени τ_с наблюдается интенсивное изменение размера режущего инструмента (например, удлинение резца), после чего температура режущего инструмента стабилизируется, и дальнейшее изменение его размера прекращается. По такому же закону происходит и изменение размеров обрабатываемой детали в связи с температурными деформациями режущего инструмента.

Например, при обработке резцом наружных цилиндрических поверхностей диаметр каждой обрабатываемой детали сначала будет прогрессивно уменьшаться, а затем после некоторого периода времени τ_с размер стабилизируется, и функциональная погрешность после момента времени τ_с превратится в постоянную погрешность.

Если обработка производится с обильным охлаждением, то погрешности обработки, вызванные температурными деформациями режущего инструмента, имеют весьма малые значения и ими можно пренебречь. При обработке деталей из штучных заготовок большое значение имеет время перерывов в работе режущего инструмента. Если время перерывов будет равно или больше времени работы инструмента, то за этот период инструмент полностью охладится, и изменение его размеров от нагрева для каждой новой детали будет носить постоянный характер и больше влиять на форму детали (например, конусность), чем на размер.

Случайные погрешности обработки возникают от многих причин, но главными из них являются упругие деформации системы СПИД и зазоры в отдельных узлах станка. Под влиянием колеблющейся силы резания, а также толчков и вибраций происходит неравномерное отжатие инструмента от обрабатываемой поверхности, а также неравномерный по величине и направлению выбор зазоров станка, что приводит к изменению размера обрабатываемой детали. Колебания силы резания возникают главным образом из-за неравномерного припуска на обработку и неравномерной твердости материала обрабатываемых деталей. Случайные погрешности, кроме перечисленных двух основных причин, возникают также в результате: неравномерности процесса резания; образования и срыва наростов на лезвии режущего инструмента; упругих деформаций детали под действием колеблющейся силы зажима; температурных деформаций обрабатываемой детали под влиянием колеблющейся температуры нагрева детали; несовпадения настроечных баз с конструкторскими; действия внутренних напряжений в материале заготовок; и других причин.

28 Суммарная погрешность механической обработки деталей на настроенных станках. Понятие мгновенного и суммарного распределения исследуемого параметра точности обработки. Теоретические диаграммы точности обработки. Условия осуществления процесса обработки, при которых он может характеризоваться диаграммой I, II, III или IV вида точности.

Таким образом, при обработке каждой новой детали возникают свои функциональные и свои случайные погрешности и, кроме того, у каждой детали имеется общая постоянная систематическая погрешность. Так как все эти погрешности возникают одновременно, то в сумме они образуют результирующую или суммарную погрешность обработки детали, которая и будет определять действительное отклонение размера от его номинального значения. В силу изменчивости функциональных и случайных погрешностей суммарная погрешность обработки одной детали будет отличаться от суммарной погрешности другой детали. В результате этого возникает рассеивание погрешностей размеров и погрешностей формы деталей в партии, обработанной с одной настройки станка. Это рассеивание может подчиняться различным законам распределения. В частности, для погрешностей размеров часто находит применение закон нормального распределения. Выбор закона нормального распределения для исследования погрешностей размера обосновывается теоремой Ляпунова, которую для рассматриваемого случая можно упрощенно представить следующим образом. Если наблюдаемая величина х является суммой частных величин x_i, вызванных действием значительного числа случайных и некоторого числа систематических факторов; если влияние всех случайных факторов на суммарную величину одного порядка, т. е. среди них нет резко доминирующих; если случайные факторы взаимно независимы и число их не изменяется во времени; если число систематических факторов остается одинаковым и постоянным во времени, то при выполнении этих условий и при достаточно большом числе слагаемых сумма последних будет следовать закону нормального распределения. Причем из теоремы Ляпунова следует, что каждое слагаемое может иметь какое угодно распределение. Сумма же их будет подчиняться закону нормального распределения, если число слагаемых достаточно велико и выполняются остальные условия теоремы Ляпунова.

Опыты показывают, что при работе на настроенных станках, когда среди возникающих случайных погрешностей обработки нет резко доминирующих и систематические погрешности не изменяются существенно во времени, когда работа протекает в нормальных условиях (станок, приспособление, инструмент находятся в исправном и хорошем состоянии), то распределение действительных размеров партии деталей, обработанных на станке с одной настройки, подчиняется обычно закону нормального распределения.

Отступление от нормального закона распределения действительных размеров партии деталей может быть вызвано в основном тремя причинами:

1) наличием доминирующей случайной погрешности или доминирующей систематической погрешности, закономерно изменяющейся во времени;

2) наличием переменного рассеивания из-за неполадок в станке или резкого колебания механических свойств материала обрабатываемых заготовок;

3)одновременным действием первой и второй причин.

Под мгновенным распределением понимается такое распределение изучаемого признака в генеральной совокупности, которое имело бы место, если бы действие всех производственных факторов оставалось таким (или примерно таким), каким оно является в данный момент времени. Другими словами, функциональные погрешности оставались бы постоянными и равными по величине тому значению, какое они имеют в данный момент. Поэтому мгновенное распределение по существу является распределением только случайных погрешностей обработки.

Под суммарным распределением обычно понимается итоговое распределение изучаемого признака в партии деталей, изготовленных за период времени от наладки до подналадки станка.

Строго говоря, рассеивание случайных погрешностей тоже будет несколько изменяться во времени вследствие износа режущего инструмента и в связи с этим сопровождаться некоторым увеличением силы резания. Однако это увеличение рассеивания случайных погрешностей во времени будет настолько незначительным, что для большинства операций с ним практически можно не считаться. С учетом изложенного изменение во времени суммарной погрешности обработки и ее основных составляющих при обработке наружных цилиндрических поверхностей на настроенных станках токарной группы можно выразить при помощи четырех типов теоретических точностных диаграмм упрощенного вида (рис. 5). Упрощения заключаются в том, что изменения функциональных погрешностей приняты по линейному закону, а рассеивание случайных погрешностей - постоянным во времени.

На диаграммах по оси абсцисс отложено время работы станка в минутах с момента его пуска, а по оси ординат - отклонения размеров деталей от номинала в микронах. Линия 1, параллельная оси абсцисс, определяет постоянные погрешности, линии 2 и 4 определяют пределы рассеивания случайных погрешностей, а линия 3 характеризует изменение среднего значения суммарной погрешности обработки под влиянием функциональных погрешностей. Точка τ₀ на оси абсцисс (см. рис. 5, б) соответствует моменту пуска станка; точка τ₁ соответствует времени наступления стабилизации температуры резца, когда дальнейшее удлинение его от нагрева прекращается, и времени окончания ускоренного первичного износа резца; точка τ_k соответствует времени окончания работы станка в связи с необходимостью его подналадки. С правой стороны диаграммы для времени τ_k показаны величины суммарной погрешности обработки Δ и ее составляющих Δ_n, Δ_f и Δ_c. Для обработки отверстий диаграммы будут иметь аналогичный вид, но повернуты на 180° относительно оси абсцисс.

Диаграмма типа I на рис. 5, а характерна для случая, когда работа производится с охлаждением доведенным резцом, т. е. отсутствует его начальный износ и удлинение от нагрева. Этот тип диаграммы возможен и при работе без охлаждения доведенным резцом при условии, что время перерывов будет равно или больше времени работы резца.

Рис. 5. Теоретические диаграммы точности обработки наружных цилиндрических поверхностей на настроенных станках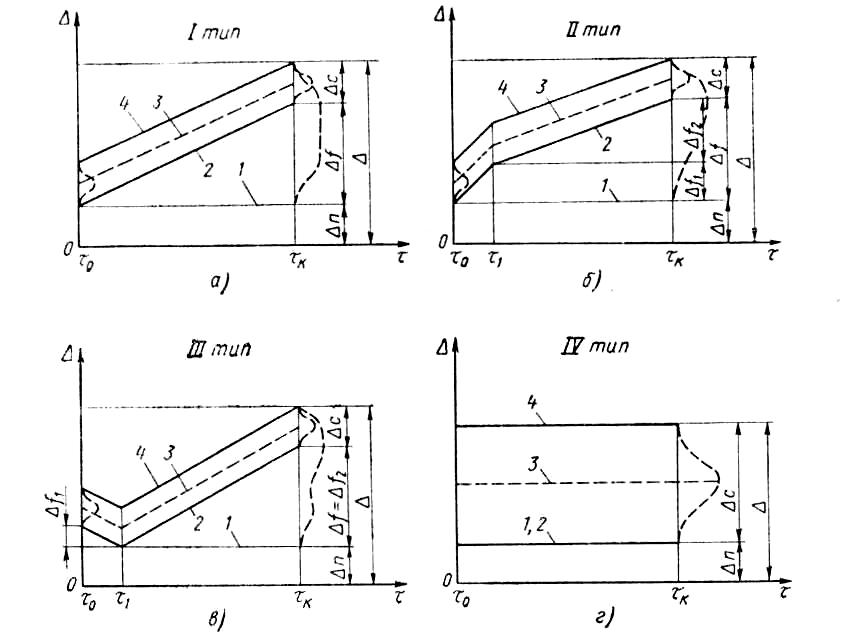

Диаграмма типа II на рис. 5, б характерна для случаев, когда работа производится недоведенным резцом с охлаждением или без охлаждения, но при этом удлинение его от нагрева в момент стабилизации температуры по величине меньше размерного износа за этот же отрезок времени (τ₁ – τ₀) либо при работе без охлаждения недоведенным резцом, когда время перерывов равно или больше времени работы резца.

Диаграмма типа III (рис. 5, в) имеет место тогда, когда работа производится без охлаждения доведенным или недоведенным резцом, удлинение которого от нагрева в момент стабилизации температуры по своей величине больше размерного износа его за тот же период времени τ₁ – τ₀).

Диаграммы I, II и III типа отражают характер изменения погрешностей обработки во времени с момента пуска станка. Если же станок уже предварительно проработал некоторое время (τ > τ₁), то для всех трех случаев будет иметь место только один первый тип диаграммы.

Диаграмма типа IV на рис. 5, г может иметь место тогда, когда отсутствуют функциональные погрешности. Такие случаи возможны, например, при обработке очень мелких деталей с весьма малым машинным временем доведенным инструментом с применением охлаждения или без охлаждения и время перерывов равно или больше времени работы инструмента, а также при обработке любых деталей на станках, оснащенных устройствами для автоматической подналадки резцов малыми импульсами.

Таким образом, в зависимости от условий обработки деталей на станке, а именно:

• наличия или отсутствия охлаждения,

• наличия доводки режущих кромок инструмента,

• длительности машинного времени и времени перерывов,

• размерной стойкости инструмента и других факторов

процессы образования погрешностей обработки во времени с момента пуска станка можно выразить графически при помощи четырех типов теоретических диаграмм точности. В соответствии с этим можно все процессы механической обработки разбить по точности на четыре типа, имея при этом в виду образование погрешностей обработки с момента пуска станка. Такое деление процесса по точности на типы имеет большое значение для расчленения суммарной погрешности обработки на составные ее части и для определения настроечного размера.

Для анализа же точности и устойчивости процессов механической обработки, когда исследования ведутся после того, как станок уже проработал некоторое время (τ > τ₁) возможны только два вида процессов, характеризуемых диаграммами I или IV типа. В ряде случаев точностные диаграммы могут иметь отступления от рассмотренных четырех типов. Для выявления и устранения причин таких отступлений могут быть полезными точностные диаграммы проф. Н. А. Бородачева, которые приведены в справочнике «Машиностроение»⁴.

29. Понятие устойчивости процесса обработки во времени. Технологическая и статистическая устойчивость процесса обработки во времени. Задачи и методы статистического анализа точности механической обработки. Общие положения методов большой выборки, малых выборок и точечных диаграмм (контрольных карт).

Под устойчивостью процесса во времени следует понимать его свойство без дополнительных регулировок сохранять требуемую точность за время обработки партии деталей с одной настройки станка.

Необходимо различать два вида устойчивости процессов во времени: технологическую и статистическую.

Процесс является технологически устойчивым, если за время обработки настроечной партии все размеры деталей находятся в пределах допуска. Процесс является статистически устойчивым, если за время обработки настроечной партии статистические характеристики рассеивания размеров деталей, т. е. дисперсия случайных погрешностей s² и средняя арифметическая суммарной погрешности обработки сохраняют постоянство своих значений, другими словами, если течение процесса во времени характеризуется теоретической диаграммой точности IV типа.

Кроме таких, полностью статистически устойчивых процессов, на практике встречаются процессы, у которых только дисперсия случайных погрешностей остается постоянной во времени, а среднее значение закономерно изменяется во времени, т. е. процессы характеризуются диаграммами точности I, II и III типа. Такие процессы будем в дальнейшем называть статистически устойчивыми по рассеиванию.

Очевидно, что статистически устойчивый процесс, а также статистически устойчивый процесс только по рассеиванию, при наличии закономерного изменения во времени центра рассеивания, будет при надлежащей точности и устойчивым технологически. Но процесс, устойчивый технологически, может быть не устойчивым статистически полностью или частично. Для того чтобы процесс был точен и можно было бы систематически наблюдать за его точностью во времени, необходимо, чтобы он был либо полностью, либо частично статистически устойчивым. Другими словами, необходимо добиться таких условий течения процесса во времени, при которых он приближался бы к одной из четырех типов теоретических диаграмм точности.

Основными задачами статистического анализа являются: 1 установление вида статистической устойчивости процесса, выявление причин неустойчивости процесса во времени, приведение его в устойчивое состояние; 2 определение точности процесса.

Статистический анализ устойчивости и точности процесса может быть осуществлен тремя основными методами: методом больших выборок, методом малых выборок и методом точечных диаграмм.

Сущность статистического анализа посредством большой выборки заключается в следующем. После того, как станок проработает время, необходимое для стабилизации температуры системы СПИД, из его текущей продукции берется большая выборка деталей (n ≥ 50), изготовленных подряд одна за другой при неизменной настройке и других неизменных условиях, и вычисляются статистические характеристики выборки и s. Далее проверяются гипотезы о случайности выборки и нормальном распределении. Если эти гипотезы подтверждаются, то процесс считается устойчивым во времени и его относят к IV типу точности. При отрицательных результатах проверки гипотез проводят исследования по определению, к какому типу точности (I, II или III-му) может быть отнесен рассматриваемый процесс. Определяется погрешность обработки, исходя из типа точностной диаграммы, выявляются причины большой погрешности обработки или неустойчивости процесса и вырабатываются рекомендации по их устранению.

В отличие от метода больших выборок статистический анализ посредством малых выборок предусматривает взятие в течении смены или иного периода работы станка выборок объемом n = 5-10 шт. через определенные фиксированные промежутки времени (например, через 15 – 30 мин.). Каждая выборка проверяется на случайность, а для каждых двух смежных выборок проверяется гипотеза однородности дисперсий. Сравнивая и оценивая расхождения средних и дисперсий выборок, можно установить моменты разладок процесса и даже источники этих разладок. Устраняя причины разладок, можно привести его в состояние, когда рассеивание размеров в каждый момент времени будет носить более или менее стабильный характер. Метод малых выборок, если последние берут регулярно в течение исследуемого периода (например, рабочей смены), позволяет получить полную картину состояния процесса, выяснить степень его устойчивости, а также выявить причины недостаточной устойчивости процесса во времени. Основным достоинством метода малых выборок является возможность отслеживать динамику изменения точности процесса во времени, чего нельзя сделать с помощью метода больших выборок. Последний может дать представление лишь о точности и устойчивости процесса в период взятия выборки, которые могут сохраниться и в дальнейшем, если после взятия выборки условия протекания процесса не изменяются. В действительности такой неизменности производственных условий заранее предвидеть нельзя.

В методе точечных диаграмм также используются малые текущие выборки, но оценка полученных данных осуществляется визуально по построенным точечным диаграммам изменения отклонений размера деталей или их средних значений, или размахов отклонений размера за время наблюдений. Метод точечных диаграмм не требует выполнения вычислительных работ, связанных с проверкой различных гипотез (случайности выборок, однородности средний и др.), что обеспечивает удобство и простоту контроля над ходом процесса обработки в производственных условиях.

1 Бородачев Н.А. Основные вопросы теории точности производства. М.-Л.: Изд-во АН СССР, 1950.

2 Романовский В.И. Применение математической статистики в опытном деле. М:, Гостехиздат, 1947.

31. Дунин-Барковский И.В., Смирнов Н.В. Теория вероятностей и математическая статистика в технике. М.: Гостехиздат,1955.

4 Энциклопедический справочник «Машиностроение». Том 15, М.: Машгиз, 1951.