Оглавление
Сигналы 2
Дискретное преобразование Фурье 5
Спектры аналоговых и дискретных сигналов 7
Дискретные системы 9
Проектирование дискретных систем. 12
КИХ фильтры. 12
Проектирование дискретных систем. 14
БИХ фильтры. 14
Операции над спектрами сигналов при их цифровой обработке 16
Изменение частоты дискретизации цифрового сигнала 18
Увеличение частоты дискретизации (Интерполяция) 18
Уменьшение частоты дискретизации (Децимация) 20
Определение разрядности АЦП и ЦАП для вычислителей 22
цифровых фильтров 22
Ошибки квантования в цифровых фильтрах 24
Сигналы 2
Дискретное преобразование Фурье 5
Спектры аналоговых и дискретных сигналов 7
Дискретные системы 9
Проектирование дискретных систем. 12
КИХ фильтры. 12
Проектирование дискретных систем. 14
БИХ фильтры. 14
Операции над спектрами сигналов при их цифровой обработке 16
Изменение частоты дискретизации цифрового сигнала 18
Увеличение частоты дискретизации (Интерполяция) 18
Уменьшение частоты дискретизации (Децимация) 20
Определение разрядности АЦП и ЦАП для вычислителей 22
цифровых фильтров 22
Ошибки квантования в цифровых фильтрах 23
Сигналы
Аналитическая запись дискретного сигнала
а
|
|
б
|
|
в
|
|
Дискретный сигнал квантованный по времени
а |
|
б |
|
в |
|
г |
|
Примеры дискретных сигналов
а |
|
б |
|
в |
|
г |
|
Аналитическая запись цифровых последовательностей
а |
|
б |
|
в |
|
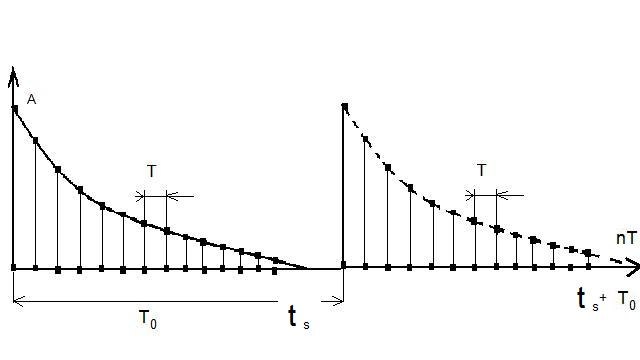
Периодическая последовательность и её особенности
а |
|
б |
|
в |
|
Сдвиг последовательности
Если последовательность x(nT)={1,2,3,0,0,0} с периодом N=6 сдвинуть вправо на 2 отсчёта то получим:
а |
x(nT)={1,2,0,0,0,3} |
б |
x(nT)={0,0,1,2,0,3} |
в |
x(nT)={0,0,1,2,3,0} |
г |
x(nT)={3,0,0,0,1,2} |
Дискретное преобразование Фурье
1. Для каких сигналов используется ДПФ:
а |
аналоговых |
б |
аналоговых периодических |
в |
дискретных периодических |
2. Прямое дискретное преобразование Фурье:
а |
|
б |
|
в |
|
,
где k=0,
1,
2, …N-1
,
где
n=0,
1,
2, …N-1
,
где
k=0,
1,
2, …N-1
3. Обратное ДПФ:
а |
|
б |
|
в |
|
,
где n=0,
1,
2, …N-1
,
где n=0,
1,
2, …N-1
,
где n=0,
1,
2, …N-1
4. Использование ДПФ для получения свертки сигналов x1(nT) и x2(nT)
а |
для
последовательности
|
б |
последовательность (nT) умножить на (nT), затем взять ДПФ от произведения (nT)* (nT), далее взять обратное ДПФ и получить свертку сигналов (nT) и (nT) |
в |
для последовательности (nT) определить прямое ДПФ (k), умножить (k) на вторую последовательность (nT), затем определить обратное ДПФ от полученного произведения и получить свертку сигналов (nT) и (nT) |
г |
для последовательности (nT) определить прямое ДПФ, затем умножить его на первую последовательность (nT), далее определить обратное ДПФ от произведения и получить свертку двух последовательностей (nT) и (nT) |
(nT)
определить ДПФ
(k),
для последовательности
(nT)
определить ДПФ
(k),
затем перемножить
(k)*
(k)=Y(k)
и взять обратное ДПФ от Y(k)
и получить y(nT)5. Какие Вы знаете алгоритмы вычисления ДПФ:
а |
Прореживание
по времени и по частоте, при этом длина
последовательности должна быть кратной
|
б |
Прореживание по времени и по частоте, длина последовательности может быть любой |
в |
Прореживание по времени и по частоте, длина последовательности должна быть четной 2ν , где ν – целое число 1, 2, 3, … |
г |
Прореживание по времени и по частоте, длина последовательности должна быть нечетной 2ν+1, где ν – целое число 1, 2, 3, … |
,
где ν – целое число 1, 2, 3, …