
- •1. Функции от матриц.
- •2. Интерполяционный полином Лагранжа-Сильвестра
- •3.Скелетное разложение матрицы: лемма о ранге, лемма о существовании и неединственности скелетного разложения
- •5. Теорема о существовании псевдообратной матрицы Мура-Пенроуза.
- •6. Теорема о единственности псевдообратной матрицы Мура-Пенроуза
- •7. Свойства псевдообратной матрицы Мура-Пенроуза
- •8. Решение однородных систем линейных алгебраических уравнений с использованием псевдообратной матрицы Мура-Пенроуза
- •9. Нормальное псевдорешение системы линейных алгебраических уравнений.
- •12. Сопряженное пространство и его базис
- •13. Ортогональное дополнение сопряженного пространства
- •14. Сопряжённое отображение
- •15. Унитарные и ортогональные матрицы. Их свойства
- •16. Критерии унитарности матрицы
- •17. Унитарное подобие.
- •18. Теорема Шура об унитарной триангуляризации матриц
- •19. Спектральная теорема для нормальных матриц
- •20. Эрмитовы и косоэрмитовы матрицы. Их свойства. Эрмитово разложение
- •21. Критерии эрмитовости матрицы
- •22. Теорема Рэлея-Ритца
- •23. Сингулярное разложение матриц
- •24. Полярное разложение матриц
- •25. Векторные нормы. Непрерывность векторных норм
- •26. Эквивалентностьвекторныхнорм
- •27. Матричные нормы
- •28. Согласованные и подчиненные векторные и матричные нормы.
- •29. Число обусловленности.
- •30. Сходимость матриц
- •31. Теорема Гершгорина
- •32. Уточнение оценок собственных значений с помощью преобразования подобия.
- •33. Локализация собственных значений Неравенство Шура. Теорема Бендиксона.
- •34. Локализация собственных значений Теорема Гирша. Теорема Брауна.
- •35. Невырожденность матриц.
- •36. Неотрицательные и положительные матрицы, их свойства.
- •37.Сравнение спектральных радиусов неотрицательных матриц
- •38.Теорема Перрона (с доказательством)
- •39.Теорема Перрона-Фробениуса
- •40.Теорема Фань-Цзы.
- •41.Примитивные и импримитивные матрицы.
- •42.Стохастические матрицы.
- •1. Функции от матриц.
- •2. Интерполяционный полином Лагранжа-Сильвестра
- •3. Скелетное разложение матрицы: лемма о ранге, лемма о существовании и неединственности скелетного разложения
- •21. Критерии эрмитовости матрицы
21. Критерии эрмитовости матрицы
Матрица A ∈ эрмитова тогда и только тогда, когда выполнено хотя бы одно из следующих условий:
а) функция
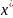 Ax
принимает вещественные значения для
любого x
∈
Ax
принимает вещественные значения для
любого x
∈
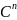 ;
;
b) матрица A нормальна и все ее собственные значения вещественны;
с) матрица
 AS
эрмитова для любой матрицы S
∈
.
AS
эрмитова для любой матрицы S
∈
.
Доказательство. Необходимость.
Рассмотрим число, комплексно-сопряженное к числу Ax:
 =
=
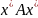 =
=
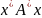 =
Ax
=
Ax
Таким образом, число x∗Ax совпадает с комплексно сопряженным числом и, следовательно, является вещественным.
Пусть λ - собственное значение эрмитовой матрицы A, x -соответствующий ему нормированный собственный вектор: Ax = λx, x = 1.
Умножим второе равенство на λ:
λ = λ x = λx = Ax ∈ R (в силу доказанного утверждения a). Нормальность матрицы А вытекает из справедливости равенства: = (A = , = A) = .
Для произвольной матрицы S ∈ справедливо:
 =
=
 S =
S =
 ,
следовательно
- эрмитова.
,
следовательно
- эрмитова.
Достаточность.
Рассмотрим
утверждение а) для вектора (x + y) ∈
:
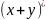 A(x
+ y)
= (
Ax
+
A(x
+ y)
= (
Ax
+
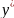 Ay)
+ (
Ay
+
Ax)
∈
R
∀x,y
∈
.
Поскольку
Ax
∈ R,
Ay
∈ R по предположению, то
Ay
+
Ax
∈ R, ∀ x,y ∈
.
(6.1)
Ay)
+ (
Ay
+
Ax)
∈
R
∀x,y
∈
.
Поскольку
Ax
∈ R,
Ay
∈ R по предположению, то
Ay
+
Ax
∈ R, ∀ x,y ∈
.
(6.1)
Возьмем в (6.1) x =
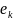 ,
y =
,
y =
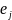 (
-
k-й вектор естественного базиса
.):
(
-
k-й вектор естественного базиса
.):
 A
+
A
+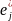 A
=
A
=
 +
+
 ∈ R ⇒ Im
= −Im
.
(6.2)
∈ R ⇒ Im
= −Im
.
(6.2)
Возьмем x = i , y = :
− i A + i A = −i + i ∈ R ⇒ Re = Re . (6.3) Из (6.2) и (6.3) следует, что = , ∀j, k = 1,…, n, а, следовательно, A = .
b)
По спектральной теореме для нормальных
матриц нормальная матрица унитарно
диагонализуема, т.е. A
=
,
где U
∈
 -
унитарная матрица, Λ
= diag{
,
..,
-
унитарная матрица, Λ
= diag{
,
..,
 }∈
}∈ ,
∈ σ
(A)
.
Рассмотрим
= (
)
,
∈ σ
(A)
.
Рассмотрим
= (
) =
=
 =
= A,
=
= A,
следовательно А - эрмитова.
c)
Положим S
=
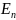 :
= (
)
⇒ A
= A
.
:
= (
)
⇒ A
= A
.
22. Теорема Рэлея-Ритца
Теорема
Рэлея-Ритца.
Пусть
Aэрмитова
и ее собственные значения упорядочены
(Пусть A
– эрмитова,
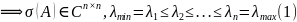 ).
Тогда
).
Тогда



Доказательство.
Поскольку матр. А – эрмитова, то по
спектральной теореме для эрмитовых
матриц сущ. такие унитарные март. и
диагональная матрица
и
диагональная матрица
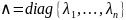 ,
что
,
что
 .
При любом векторе
.
При любом векторе
 верны равенства
верны равенства

Каждый сомножитель
 неотрицателен, поэтому
неотрицателен, поэтому

Поскольку март. U унитарна, а унитарные матр.изометричны, то имеют место равенства
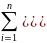
Таким образом, справедливы соотношения:

что и доказывает (2).
Покажем, что оценки в соотношении (2) точны.
Действительно, если x – собст.векторматр. A, соответствующий собственному значению λ1, то

Точность оценки сверху устанавливается аналогично.
Остальные утверждения является простыми следствиями соотношений(2).
Покажем, например,
справедливость (3). При
 из
правой части соотношения (2) имеем:
из
правой части соотношения (2) имеем:
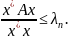
Это неравенство
обращается в равенство, когда x-
собственный
вектор матрицы A, соответствующий
собственному значению
.
Следовательно,
 .(5)
.(5)
Наконец, при можно перейти к нормированному вектору:
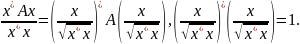
Таким образом, равенство (5) эквивалентно следующему

Рассуждения для
минимального собственного значения
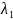 аналогичны.
аналогичны.
23. Сингулярное разложение матриц
Теорема
(Cингулярное
разложение).
Любая матрица ранга
r
может быть представлена в виде
ранга
r
может быть представлена в виде

где
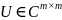 ,
,
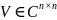 –
унитарные матр.,
–
унитарные матр.,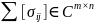 – диагональная прямоугольная матр. с
невозрастающими неотрицательными
элементами по диагонали. При этом
– диагональная прямоугольная матр. с
невозрастающими неотрицательными
элементами по диагонали. При этом
диагональные элементы σii являются сингулярными числами матрицы A;
столбцы матрицы U образуют ортонормированный базис из собственных векторов матрицы AA∗;
столбцы матрицы V образуют ортонормированный базис из собственных векторов матрицы ;
Доказательство.
Согласно свойству 70 знакоопределенных
матриц эрмитова матрица A∗A
являетсяположительнополуопределённой.
Пусть σ21,…,
σ2n
– собственные значения матрицы
причем
σi
упорядочены.Пусть v1,
. . . ,vn–
собственные векторы матрицы
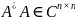 ,
соответствующие σ21,…,
σ2n.
Из спектральной теоремы для нормальныхматниц
следует, что v1,…,
vnможно
выбрать ортонормированными.
,
соответствующие σ21,…,
σ2n.
Из спектральной теоремы для нормальныхматниц
следует, что v1,…,
vnможно
выбрать ортонормированными.
По системе векторов v1,…, vnпостроим второй сингулярный базис u1,…, um(если r<m, то систему ортонормированных векторов u1,…, urдобавим до ортонормированного базиса в m-мерном пространстве.
Составим из векторов
v1,…,
vnи
u1,…,
umдве
унитарные матрицы: V ={v1,…,
vn}∈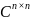 ,
U ={ и u1,…,
um}∈
,
U ={ и u1,…,
um}∈ .
Составим также диагональную матрицу
Σ=diag{σ1,
. . . ,σn}.
Тогда A=UΣV∗.
.
Составим также диагональную матрицу
Σ=diag{σ1,
. . . ,σn}.
Тогда A=UΣV∗.
