15. Унитарные и ортогональные матрицы. Их свойства

Система векторов 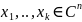называется ортогональной, если 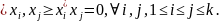Если к тому же сами векторы нормированы, т.е. 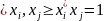, i=1,k , то акая система называется ортонормированной.

Теорема. Любая ортонормированная система ЛНЗ.

Докво. Рассмотрим для ортонормированной системы векторов {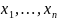 } равенство 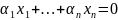и покажем, что оно возможно лишь при . Умножая равенство справа на сопряженное получим , что возможно только при 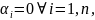откуда и вытекает ЛНЗ системы { }.

Опр. Матрица называется унитарной, если Если к тому же , то U называется ортогональной.

Теорема. (о QR-разложении). Если , n>= m, то существуют матрица c ортонормированными столбцами и верхняя треугольная матрица , такие, что A=QR. Если m=n, то Q унитарна.

Свойства унитарных матриц:

1. Для любых унитарных (ортогональных) матриц U, V 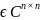произведение UVявляется также унитарной(ортогональной) матрицей.

2. Все собственные значения унитарной матрицы по модулю равны 1.

3. Любая матрица перестановок – унитарная.

Опр. Матрицей перестановок называется квадратная матрица, у которой по каждой строке и каждом столбце только один элемент отличен от нуля и равен единице.

4. Определитель унитарной матрицы по модулю равен 1

5. Унитарные матрицы одного порядка образуют группу по умножению.

16. Критерии унитарности матрицы

Матрица U ∈ C^{n × n} называется унитарной, если U*U = E. Если к тому же U ∈ R^{n × n} , то U называется ортогональной.

Теорема (о критериях унитарности). Следующие предложения эквивал. для матрицы U ∈ C^{n × n} :

a) U унитарная;

b) U невырожденная и U*=U^-1;

c) UU* = E_n ;

d) U* унитарная;

e) столбцы в U образуют ортонормированную систему;

f) строки в U образуют ортонормированную систему;

g) для любого вектора x Є Cⁿ справедливо x*x = (Ux)*(Ux)

(т.е. унитарные матрицы - изометричные). Доказательство. а) влечет b), т.к. матрица U^-1 (если она существует) - это единственная матрица, при умножении на которую слева получается E. Из определения унитарности следует, что U* именно такая матрица: UU* = UU^-1 = E. Значит, из b) следует c). Так как c) - это определение унитарности для U*, то из c) следует d).

Обращение импликаций проводится аналогично. Таким образом a), b), c) и d) эквивалентны.

Обозначим u_i - i-й столбец матрицы U. Из правил матричного умножения следует, что если U*U = E, то u_i*u_j = δ_ij, где δ_ij = - символ Кронекера. Последнее равносильно тому, что u_i,u_j ортонормированные. Следовательно, a) равносильно e). Аналогично доказывается равносильность d) и f). Докажем, что из a) следует g). Возьмем y = Ux. Тогда

y*y = x*U*Ux = x*x. Докажем, что из g) следует a). Рассмотрим сначала случай n = 2. Рассмотрим произвольную матрицу U, для которой выполняется g) для ∀x ∈ Cn. Возьмем

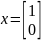
Имеем: 1 = x*x = y*y = x*U*Ux - это элемент матрицы U*U в позиции [1,1]. Аналогично полагая получим U*U₍₂₂₎ = 1. Т.е. U*U имеет вид , где a - скалярное произведение 1-го и 2-го столбца, - 2-го и 1-го столбца. Положим

Тогда из g) следует 2 = x*x = y*y = x*U*Ux =

Рассматривая , будем иметь

2 = x*x = y*y = x*U*Ux = 2 + i(a − ) ⇒ a − = 2i Im a = 0. Таким образом + a = 2 Re a = 0, a − = 2i Im a = 0 ⇒ a = 0. Следовательно, при n = 2 в случае выполнения g) имеем UU* = E, т.е. верно а). Рассмотрим теперь случай n > 2. Пусть U ∈ C^{n × n} матрица, для которой выполняется g). Положим A = U*U. Возьмем x ∈ Cⁿ, в котором все компоненты нулевые, кроме i-й и j-й (i ≤ j). Тогда где A_{j,j} главная подматрица матрицы A в строках i,j и столбцах i,j. Из доказанного выше при n = 2 следует, что A_{j,j} = E₂ ∈ C^{n × n}. Так как i,j - произвольные, то в A любая главная подматрица порядка 2 совпадает с E². Единственная матрица, обладающая таким свойством - это матрица E_n.

Случай n = 1 очевиден.