13. Ортогональное дополнение сопряженного пространства

Опр. Пусть -произвольное подпространство векторного пространства . Множество ковекторов из , которые ортогональны всем векторам из , называется ортогональным дополнением к пространству и обозначается : .

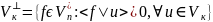Другими словами, ортогональное дополнение к - это множество всех линейных функций из .,обращающихся в нуль на векторах из

К тому же, ортогональное дополнение к .

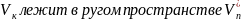Теорема. Ортогональное дополнение подпространства является подпространством пространства , при этом

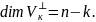
Док-во. Пусть - произвольный ковектор из ортогонального дополнения. Покажем, что ортогональность ковектора f всем векторам из равносильна ортогональности fвекторам любого базиса в .

Пусть -некоторый базис в тогда для любого вектора справедливо разложение , и в силу линейности функции f справедливо

<f|u>==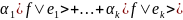 . Откуда следует, что <f|u>=0 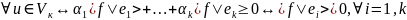(1)

Т.о. произвольный ковектор является решением системы (1). Для заданного базиса с базисными векторами вида система (1) равносильна системе линейных алгебраических уравнений: 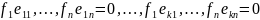(2).

Так как векторы ЛНЗ, то ранг матрицы системы(2) равен k. как известно из линейной алгебры, множество решений системы (2) образует линейное пространство размерности n-k. Это равносильно доказываемому утверждению.

14. Сопряжённое отображение

Пусть дано линейное отображение А: → .

Опр. Отображение 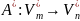называется сопряженным отображением для А, если для любого и для любого выполняется следующее соотношение: .

Теорема. Для любого заданного линейного отображения А сопряженное отображение существует, линейно и единственно.

Докво. Построим отображение удовлетворяющему условию для заданного отображения А. Для того чтобы задать отображение , надо для каждого функционала указать соотвествующий ему функционал 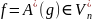, являющийся образом g при отображение . Но надо задать функционал из .—это значит определить его действие на произвольный вектор . Зададим правило этого действия. С учетом определяющего соотношения для сопряженного отображения имеем: .

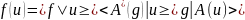Из этого следует, что для данного функционала действие искомого функционала на произвольный вектор определяется следующим образом. Сначала применим отображение А: → к вектору , в результате чего получаем его образ – вектор . Затем вычисляем значение заданного функционала на векторе и получаем значение <g|A(u)>, что является результатом действия f на u.

Т.о. сопряженное отображение определяется как композиция 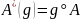. Т.к. выполняются эти условия: 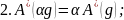, то можем утверждать, что данное отображение будет линейным.

Докажем единственность .

Пусть -- два отображения, для которых справедливо . Тогда для всех . Отсюда следует, что <( |u>=0. Фиксируем g и будем менять u. Тогда элемент (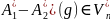 . Как линейная функция на принимает только нулевые значения, и, значит, равен нулю. Поэтому 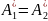, что доказывает единственность и завершает доказательство теоремы.

Теорема. Пусть А: → – линейное отображение Е и Н – базисы пространств и , соответственно, - биортогональные базисы пространства и . Тогда если отображение А в базисах Е и Н имеет матрицу А, то сопряженное отображение в биортогональных базисах и имеет матрицу .