9. Нормальное псевдорешение системы линейных алгебраических уравнений.

Опр. Вектор r=b-Ax называется невязкой вектора х.

Длина невязки ||r|| характеризует, насколько вектор х близок к решению систему. Если х является решением системы, то невязка равно нулю. Если система несовместна, то невязка всегда будет ненулевой. В этом случае можно поставить задачу: найти такой вектор х⁰, что величина ||r||²=||b-Ax⁰||² примет наименьшее значение. Такой подход называют методом наименьших квадратом.

Опр. Вектор х⁰, длина невязки которого минимальна, наз. Псевдорешением системы Ах=b. Псевдорешение с минимальной длиной называется нормальным псевдорешением системы Ax=b.

Теорема. Нормальное псевдорешение системы Ах=b всегда существует, единственно и определяется по формуле х⁰ =

10. Матричные уравнения AX = XB

Рассмотрим матричное уравнение AX=XB, .

Рассмотрим элементарные делители матрицы

А: и элементарные делители матрицы В:

.

Теорема. Общее решение уравнение АХ=ХВ, где

A=U , B=V ,

, может быть найдено по формуле Х=U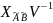 . Здесь -общее решение уравнение

Если , то , если , то - произвольная верхняя треугольная матрица.

Матрица Х зависит от N произвольных параметров : Х= , где ,

Следствие. Если матрицы А и В не имеют одинаковых собственных значений, то уравнение АХ=ХВ имеет только нулевое решений, то есть Х=0.

11. Матричные уравнения AX = XA

Рассмотрим частный случай уравнения АХ=ХВ при В=А: АХ=ХА .

Теорема. Общее решение АХ=ХВ, где , А=U , может быть найдено по формуле . Здесь -общее решение ур-ния. .

Если , то , если , то - произвольная правильная верхняя треугольная матрица. Матрица Х зависит от N произвольных параметров, N= , где

Теорема. Число ЛНЗ матриц, перестановочных с матрицей , определяется формулой N=n₁+3n₂+5n₃+…+(2t-1)n_t, где - непостоянные инвариантные множители матрицы А, .

Замечание. Ясно, что m=n₁+n₂+…+n_t. Отсюда следует, N≥m, причем N=m равносильно t=1, то есть все элементарные делители матрицы А взаимно просты.

12. Сопряженное пространство и его базис

Пусть – линейное векторное пространство над полем , .

Опр. Числовая функция y=f(u) с аргументами из и значениями из поля называется линейной функцией на пространстве , если: ;

.

Опр. Пространство линейных функций, определенных на векторном пространстве называется сопряженным пространством к и будем обозначать .

Функции из пространства . Называют ковекторами, а само выражение <f|u> называют скалярным произведением вектора с ковектором.

Опр. Вектор u и ковектор f называются ортогональным друг другу, если <f|u>=0.

Функционалы называются координатными функционалами базиса { }. Для них (1). Соотношение (1) называются соотношениями биортогональности, а система векторов E={ } и F={ }, удовлетворяющие (1) –биортогональными, что обозначаются как E F.

Теорема. Координатные функционалы , линейно независимы и составляют базис в .

Следствие. Для любого базиса Е пространства сузествует, и притом только один, базис F пространства , такой что E F.

Опр. Базис и F={ }, построенный из координатных функционалов базиса { }. В , называется сопряженным базисом для Е.