
- •1. Функции от матриц.
- •2. Интерполяционный полином Лагранжа-Сильвестра
- •3.Скелетное разложение матрицы: лемма о ранге, лемма о существовании и неединственности скелетного разложения
- •5. Теорема о существовании псевдообратной матрицы Мура-Пенроуза.
- •6. Теорема о единственности псевдообратной матрицы Мура-Пенроуза
- •7. Свойства псевдообратной матрицы Мура-Пенроуза
- •8. Решение однородных систем линейных алгебраических уравнений с использованием псевдообратной матрицы Мура-Пенроуза
- •9. Нормальное псевдорешение системы линейных алгебраических уравнений.
- •12. Сопряженное пространство и его базис
- •13. Ортогональное дополнение сопряженного пространства
- •14. Сопряжённое отображение
- •15. Унитарные и ортогональные матрицы. Их свойства
- •16. Критерии унитарности матрицы
- •17. Унитарное подобие.
- •18. Теорема Шура об унитарной триангуляризации матриц
- •19. Спектральная теорема для нормальных матриц
- •20. Эрмитовы и косоэрмитовы матрицы. Их свойства. Эрмитово разложение
- •21. Критерии эрмитовости матрицы
- •22. Теорема Рэлея-Ритца
- •23. Сингулярное разложение матриц
- •24. Полярное разложение матриц
- •25. Векторные нормы. Непрерывность векторных норм
- •26. Эквивалентностьвекторныхнорм
- •27. Матричные нормы
- •28. Согласованные и подчиненные векторные и матричные нормы.
- •29. Число обусловленности.
- •30. Сходимость матриц
- •31. Теорема Гершгорина
- •32. Уточнение оценок собственных значений с помощью преобразования подобия.
- •33. Локализация собственных значений Неравенство Шура. Теорема Бендиксона.
- •34. Локализация собственных значений Теорема Гирша. Теорема Брауна.
- •35. Невырожденность матриц.
- •36. Неотрицательные и положительные матрицы, их свойства.
- •37.Сравнение спектральных радиусов неотрицательных матриц
- •38.Теорема Перрона (с доказательством)
- •39.Теорема Перрона-Фробениуса
- •40.Теорема Фань-Цзы.
- •41.Примитивные и импримитивные матрицы.
- •42.Стохастические матрицы.
- •1. Функции от матриц.
- •2. Интерполяционный полином Лагранжа-Сильвестра
- •3. Скелетное разложение матрицы: лемма о ранге, лемма о существовании и неединственности скелетного разложения
- •21. Критерии эрмитовости матрицы
36. Неотрицательные и положительные матрицы, их свойства.
Определение.
Матрица A = [aij]
∈ называется
неотрицательной
(положительной)
и это обозначается как А≥0 (А>0), если
аij≥0
(аij>0),
i=1,n,j=1,m.
называется
неотрицательной
(положительной)
и это обозначается как А≥0 (А>0), если
аij≥0
(аij>0),
i=1,n,j=1,m.
Аналогично определяются отношения ≤ и < понятия неположительной (отрицательной) матрицы.
Если A-B≥0 (A-B>0), то пишут А≥В (А>В).
По
определению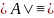 .
.
Свойства неотрицательных матриц.
Пусть А,В Є .
10. |A| ≥0 ∀A; |A| =0⇔A=0.
20.|Ax| ≤ |A| |x|.
30.|Am| ≤ |A|m, ∀m=1,2, . . .
40.Если 0≤A≤B, то 0≤Am≤Bm, ∀m=1,2, . . ..
50.Если A>0, x≥0 и x ≠0, то Ax>0.
60.Если |A| ≤ |B|, то ||A||E ≤||B||E.
70.||A||E =|||A|||E.
Теорема.
Пусть
A,B∈ .
Если
|A| ≤B, тоρ(A)≤ρ(|A|)≤ρ(B).
.
Если
|A| ≤B, тоρ(A)≤ρ(|A|)≤ρ(B).
Следствие. ПустьA, В∈ . Если 0 ≤ A ≤ B, то ρ(A)≤ρ(B).
Лемма. Пусть A∈ иA≥0. Если строчные суммы для А постоянны, то ρ(A)=||A||∞. Если для A постоянны. столбцовые суммы, то ρ(A)=||A||1.
Теорема. Пусть A∈ и A≥0. Тогда


Следствие.
Пусть A∈
,
А≥0 и
 .
Тогда
.
Тогда
 .
В частности,
.
В частности,
 если А>0 или если А неразложима и
неотрицательна.
Теорема.
Пусть A∈
и предположим, чтоА≥0. Тогда для любого
положительного вектораxЄCnсправедливы
неравенства:
если А>0 или если А неразложима и
неотрицательна.
Теорема.
Пусть A∈
и предположим, чтоА≥0. Тогда для любого
положительного вектораxЄCnсправедливы
неравенства:
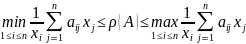
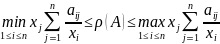
Следствие. Пусть A∈ , x ∈Rn, и предположим, что A≥0 и x>0. Если числа α,β≥0 таковы, чтоαx≤Ax≤βx, то α≤ρ(A)≤β.
Если αx<Ax, то α<ρ(A); если Ax<βx, то ρ(A) <β.
Следствие 9.4. Пусть A∈ и A≥0. ЕслиA имеет положительный собственный вектор, то отвечающее ему собственное значение есть ρ(A). Другими словами, если Ax=λx, x>0 и A≥0, то λ=ρ(A)
37.Сравнение спектральных радиусов неотрицательных матриц
Теорема Пусть A,B ∈ . Если |A| ≤ B, то ρ(A) ≤ ρ (|A|) ≤ ρ(B).
Доказательство. Во-первых, из свойств неотрицательных матриц следует справедливость следующей цепочки неравенств для ∀ m = 1, 2,... :
| |≤
|≤
 ≤
≤
 .
.
Далее из этих неравенств имеем для ∀ m = 1, 2,... :
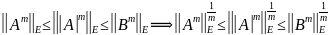
Переходя в последних равенствах к пределу при m → ∞
согласно равенству
ρ(A)
=
 получаем соотношения теоремы.
получаем соотношения теоремы.
Следствие Пусть A,B ∈ . Если 0 ≤ A ≤ B, то ρ(A) ≤ ρ(B).
38.Теорема Перрона (с доказательством)
Теорема (Перрона). Если A ∈ и A > 0, то
а) ρ(A) > 0;
b) ρ(A) есть собственное значение матрицы A
(ρ
(A)
=
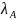 ∈
σ
(A));
∈
σ
(A));
с) для некоторого
 ∈
имеем
> 0 и A
= ρ(A)
;
∈
имеем
> 0 и A
= ρ(A)
;
d) ρ(A) есть алгебраически (а значит, и геометрически) простое собственное значение для A;
е) |λ|
< ρ(A)
для всякого собственного значения λ
 ρ(A);
ρ(A);
другими словами, только одно собственное значение , равное именно ρ(A), имеет максимальный модуль;
f )
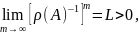 где
где
L ≡ x , Ax = ρ(A)x,
, Ax = ρ(A)x,
 y = ρ(A)y,
x > 0, y > 0,
y = ρ(A)y,
x > 0, y > 0,
 y
= 1.
y
= 1.
Доказательство:
a)- b) Рассмотрим собственное значение λ, такое, что |λ| = ρ(A) > 0, и отвечающий ему собственный вектор
x 0. По лемме(пусть еще Ax = λx, x 0 и |λ| = ρ(A). Тогда A|x| = ρ(A) |x| и |x| > 0.) искомым вектором будет |x|.
e) По определению |λ| ≤ ρ(A) для всех λ ∈ σ(A). Пусть |λ| = ρ(A) и Ax = λx, x 0.
Согласно лемме(
для некоторого θ ∈
R имеем
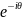 x
= |x| > 0), Aw = λw, где w =
x
> 0 для какого-то θ ∈
R. Отсюда, опираясь на следствие(Если A
имеет положительный собственный вектор,
то отвечающее ему собственное значение
есть ρ(A).др.словами λ
= ρ(A)),
получаем λ = ρ(A).
x
= |x| > 0), Aw = λw, где w =
x
> 0 для какого-то θ ∈
R. Отсюда, опираясь на следствие(Если A
имеет положительный собственный вектор,
то отвечающее ему собственное значение
есть ρ(A).др.словами λ
= ρ(A)),
получаем λ = ρ(A).
d)
ρ(A) есть собственное значение алгебраической
кратности 1; другими словами, ρ(A)—это
простой корень характеристического
уравнения
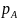 (t)
= 0, где
(t)
—характеристический полином матрицы
A.
(t)
= 0, где
(t)
—характеристический полином матрицы
A.
