28. Согласованные и подчиненные векторные и матричные нормы.

Определение. Матричная норма ||•||_M называется согласованной с векторной нормой ||•||_V , если

||A||_V≤ ||A||_M ||x||_V (1) для любой матрицы A и всех векторов x.

Определение. Пусть задана векторная норма ||•||_V. Тогда числовая функция

(2)

называется нормой матрицы, подчиненной (индуцированной) векторной норме ||•||_V.

Теорема (Подчиненная векторная норма). Функция (2) определена и является согласованной нормой в для любых норм в C^m и Cⁿ.

Теорема.Для подчиненной матричной нормы справедливо

||Ax||≤||A||||x||, ||E||=1

Доказательство

Следствие. Матричная норма ||•||_M , подчиненная векторной норме ||•||_V, согласована с этой нормой.

Матричная норма, подчиненная векторной норме ||•||_∞

Получим оценку сверху для величины ||Ax||_∞

||Ax||_∞ .

Покажем, что эта оценка достигается.

Пусть максимум по i имеет место при i=l. Возьмем x=(sign(a_l1),…,sing(a_ln)).

Имеем и точные равенства во всей цепочке выше.

Таким образом, 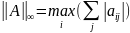подчиненная векторной норме ||•||_∞

29. Число обусловленности.

Определение. Величина

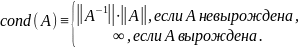(1)

называется числом обусловленности матрицы A по отношению к матричной норме ||•||.

Свойства числа обусловленности

1⁰. Для любой матричной нормы cond(A)≥1.

2⁰. Для любой матрицы A и любого числа α выполняется равенство cond(A) =cond(αA).

3⁰. Для спектральной и евклидовой норм число обусловленности не меняется при умножении матрицы слева и справа на любую унитарную матрицу.

4⁰. Для 1-, 2-, ∞-норм и евклидовой нормы число обусловленности не меняется при перестановке строк и столбцов.

5⁰. Для спектральной нормы число обусловленности любой матрицы равно отношению максимального сингулярного числа к минимальному.

30. Сходимость матриц

Определение. Матрица А называется сходящейся, если

Лемма.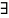 ||•||: ||A||<1 .

Доказательство.

||A^k||≤||A||^k→_k→0 0 A^k→_||•||0 A^k→_||•||∞0

Теорема.Матрица является сходящейся тогда и только тогда, когда .

Доказательство .Пусть A^k→0.Рассмотрим собственный вектор x≠0: Ax=λx. Тогда A²x=A(Ax)=A(λx)=λ(Ax)=λ²x…A^kx=λ^kx→0 .

Обратно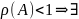 || ||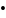:||A||<1 A^k→_k→∞0

Следствие.

31. Теорема Гершгорина

Теорема Гершгорина и ее следствия. Для произвольной матрицы AЄ обозначим - строчная почти-нормы, а также

- столбцовые почти – нормы матр. А.

Наиболее полезная и легко применяемая теорема, дающая оценка для собственных значений – теоремы Гершгорина.

Теорема Гершгорина (строчная).Все собственные значения матрицы A заключены в объединении n кругов

Кроме того, если объединение k из этих кругов есть связная область, не пересекающаяся с остальными n−k кругами, то в ней находится ровно k собственных значений матрицы A.

Теорема (Гершгорина (столбцовая)). Все собственные значения матрицы AЄ принадлежат объединению nкругов (столбцовой области Гершгорина)

Кроме того, если k из этих кругов образуют область, изолированную от остальных n-k кругов, то в ней находится ровно kсобственных значений матрицы А.