Задание 5. Корреляционный и регрессионный анализ

Корреляционно-регрессионный анализ позволяет вскрывать причины изменчивости наблюдаемых признаков и явлений, а также их взаимосвязь. С помощью этого метода устанавливается зависимость изменений изучаемых процессов от действующих на них факторов или связь отдельных признаков друг с другом.

Определить зависимость урожая капусты от пораженности ее килой

Участок	1	2	3	4	5	6	7	8	9	10
Развития болезни, %	33,5	34,2	36,0	39,3	39,9	40,5	42,3	45,8	49,7	52,8
Урожай, т/га	53,1	53,0	51,5	52,3	49,6	45,0	36,5	37,2	33,4	29,0

По предложенным результатам наблюдений провести корреляционный и регрессионный анализ данных предложенного варианта задания по следующей схеме:

1. Построить таблицу корреляционно-регрессионного анализа по представленным в варианте данным,

где: х – одна переменная, у – вторая переменная.

№ учета	х	у	х2	у2	ху
1
2
…
n
Суммы	Σх	Σу	Σх2	Σу2	Σху

2. Вычислить коэффициент корреляции r:

.

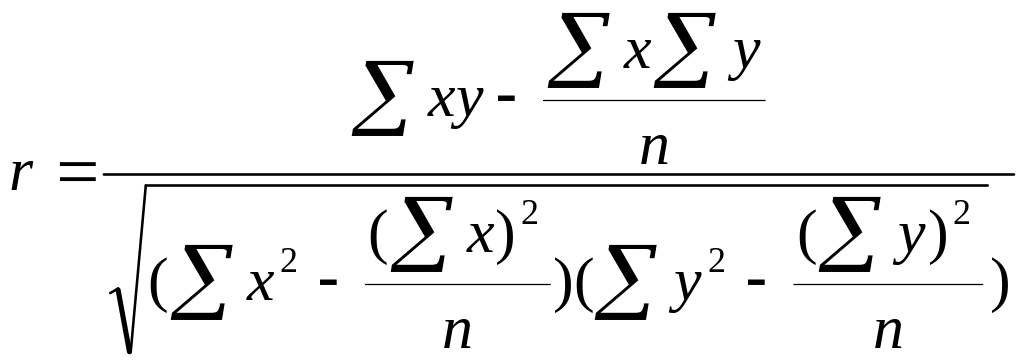где n – число парных наблюдений

3. Вычислить ошибку коэффициента корреляции S_r :

.

4. Определить существенность коэффициента корреляции по критерию t_r: (таблица Стьюдента).

5. Сделать выводы о характере и тесноте связи.

6. Вычислить коэффициент детерминации: d_xy=r²

7. Вычислить коэффициент регрессии b_x/y :

.

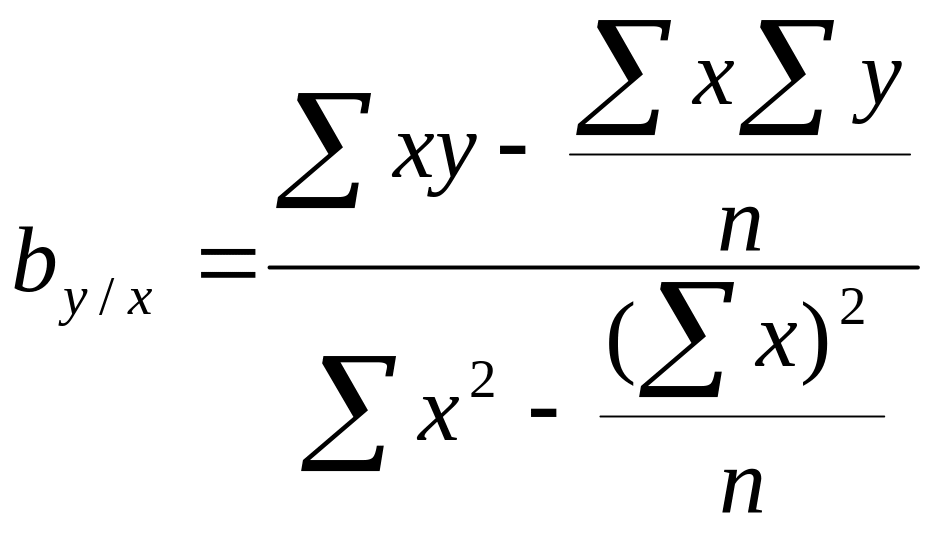8. Вычислить ошибку коэффициента регрессии S_{b y/x}:.

S_{b y/x}

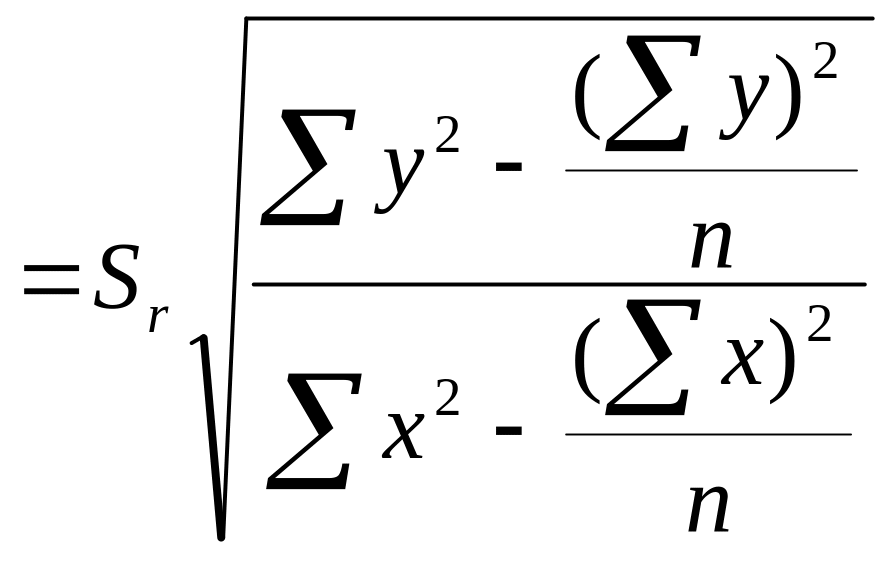
9. Составить уравнение регрессии: .

10. Определить критерий существенности коэффициента регрессии t_b и проверить t_r = t_b

.

11. Построить кривую регрессии по уравнению. Для построения линии регрессии взять 2 значения независимой переменной х, близкие к минимальному и максимальному. Подставить их по очереди в уравнение регрессии и рассчитать по уравнению соответствующие им значения зависимой переменной у. Построить систему координат, где по оси абсцисс откладываются значения х, а по оси ординат – значения у. Масштаб выбирается в соответствии с амплитудой колебаний значений изучаемых факторов. По рассчитанным 2 точкам в построенной системе координат построить линию регрессии.

12. Определить существенность регрессии по отклонению от линии регрессии и по критерию t_b.

13. Определить ошибку отклонения от регрессии

.

14. Определить доверительную зону линии регрессии: После расчета ошибки отклонения от регрессии S_ух построить доверительную зону регрессии, равную для уровня вероятности 95% у ± 2S_ух. Отложив эти значения на оси у выше и ниже линии регрессии, провести через эти точки 2 прямые, параллельные линии регрессии, ограничивающие доверительную зону. После этого нанести на график точки, соответствующие экспериментальным данным. Если они укладываются внутри доверительной зоны, значит линия регрессии существенна на уровне вероятности 95%. Если они выходят за пределы зоны, линию регрессии нельзя признать существенной.

15. Сделать выводы.