§2 Производные и дифференциалы высших порядков

1.Производные высших порядков

Определение. Пусть f(x) определена на (a,b) и имеет в некоторой окрестности точки x₀(a,b) производную g(x)=f(x). Если в точке x₀ существует g( x₀), то она называется производной второго порядка от f в точке x₀ и обозначается f(x₀). Производной n-го порядка называется производная от производной (n-1)- го порядка

.

Обозначение Лейбница .

Отметим, что для существования n-ой производной в точке, предыдущая (n-1)-я производная должна существовать в некоторой окрестности.

Аналогично определяются односторонние производные старших порядков.

Функция f называется n-раз дифференцируемой на X, если в каждой точке X существует n-ая производная.

f называется n-раз непрерывно дифференцируемой на X, если n-ая производная на X существует и непрерывна на X.

КлассыC(X), C[a,b], Cⁿ(X), Cⁿ[a,b].

Cⁿ(X) – множество всех n-раз непрерывно дифференцируемых на X функций.

Cⁿ[a,b] – множество всех n-раз непрерывно дифференцируемых на [a,b] функций. C(X)-множество всех непрерывных на X функций.

C[a,b]-множество всех непрерывных на [a,b] функций.

Пример. Вычисление второй производной функции, заданной параметрически

, x(t) строго монотонна

Аналогично вычисляются производные более высоких порядков.

Пример. Вычислить для функции

2. Вычисление производных функций, заданных неявно

Обозначим через F(x,y) некоторое выражение, содержащее параметрыx, y. Функцией, заданной неявно уравнением

F(x,y)=0 (1)

называется любая функция y=f(x) с областью определенияX , при подстановке которой в левую часть(1) это равенство превращается в тождество:

xX:F(x, f(x))=0.

Такие функции называется также однозначными ветвями.

Для вычисления производной y(x) функции, заданной неявно уравнением(1) достаточно продифференцировать тождествоF(x, f(x))=0 по переменномуx. В результате такого дифференцирования всегда будет получаться соотношение вида

A(x,y)+B(x,y)y=0 , (2)

где A(x,y), B(x,y) будут представлять собой некоторые выражения, включающие в себяx иy . Из соотношения(2) можно найти выражение дляy в нужной точке.

Пример 1: x²+y²=1, найти.

2x+2yy=0, y=. Для нахождения второй производной следует использовать равенствоx+yy=0, дифференцируя, получим

1+(y)²+yy=0, y=

Пример 2: x^y+e^xy=0

3. Формула Лейбница

Индукция по n. Для n=1 формула верна (fg)=fg+gf. Предположим, что формула доказана для n. Вычислим n+1 производную

Пример: найти f⁽¹⁰⁰⁾(x) для функции f(x) = x²e^x.

4.Дифференциалы высших порядков

dx=x=x - x₀ , dy=f(x₀)dx, x-независимое переменное

Определение. d ²f = f dx², dx=x, d ⁿf=d(d ^n-1 f)=d(f ^(n-1)dx^n-1)=f ⁽ⁿ⁾dxⁿ

при вычислении последующих дифференциалов приращение dx=x берется одно и тоже.

Из определения следует, что

, что согласуется с обозначением Лейбница.

Замечание. Если x – независимое переменное, то dⁿ x = 0, при n=2,3,…

Простейшие свойства дифференциалов

1. d(u+v)=du+dv, d(uv)=udv+vdu ,

2. dⁿ(cu)=c dⁿ u, c=const

3. dⁿ(u+v)=dⁿ u+ dⁿ v

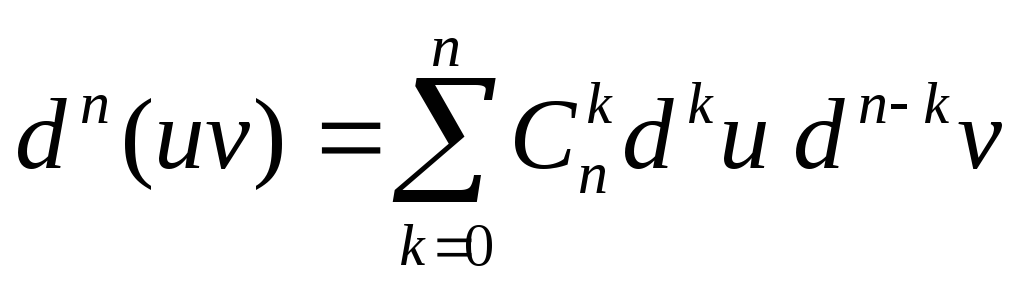4. ,d ⁰u=u, d ⁰v=v.

5.Инвариантность формы дифференциала первого порядка

Пусть задана сложная функция y=F(t)=f(g(t)), y=f(x), x=g(t).

dy=(f(g(t)) dt=f(x)g(t)dt=f(x)dg=f(x)dx. Вид первого дифференциала такой же, как и в случае, когда x является независимой переменной. Это свойство называется свойством инвариантности дифференциала первого порядка.

Для дифференциалов высших порядков свойства инвариантности, вообще говоря, нет.

dy=fdx, d ²y=fdx²+fd ²x, для функции x=t², второй дифференциал d ²x  0.

Замечание. (Важный частный случай, когда свойство инвариантности наблюдается и для старших дифференциалов ). В случае, когда внутренняя функция суперпозиции линейна, свойство инвариантности сохраняется для дифференциалов произвольных порядков.

d ⁿy, y=f(x), x=at+b, dx = a dt, d ²x=…=d ⁿx=0. Таким образом, n-ый дифференциал

d ⁿf=f⁽ⁿ⁾dxⁿ имеет такой же вид, как и в случае независимого переменного x.