Конспект лекций Логинов А.С. ЭТФ 1 семестр loginov_1999@mail.ru

Глава 1. Ведение

§1. Некоторые понятия теории множеств и математической логики

1.Множество, операции над множествами, обозначения

Множество - совокупность некоторых различимых объектов. Задать множество - задать признаки, характеризующие эти объекты.

Примеры:

N - натуральные числа, Z - целые числа, Q - рациональные числа,

R - вещественные числа

[a,b] – отрезок, (a, b) – интервал, (a,b],[a,b) – полуинтервалы.

Элемент принадлежит множеству x E, элемент не принадлежит множеству x E

Подмножество A  E

- пустое множество E, EE

Обозначение множества перечислением - {a, b, c}

Обозначение множества указанием характеризующего свойства –

{ x : x удовлетворет свойству P}.

Пример: N={xZ:x>0}, [a,b]={x: axb}

Дополнение (разность) E\A={xE:xA}

Пересечение AB ={x:xA и xB}

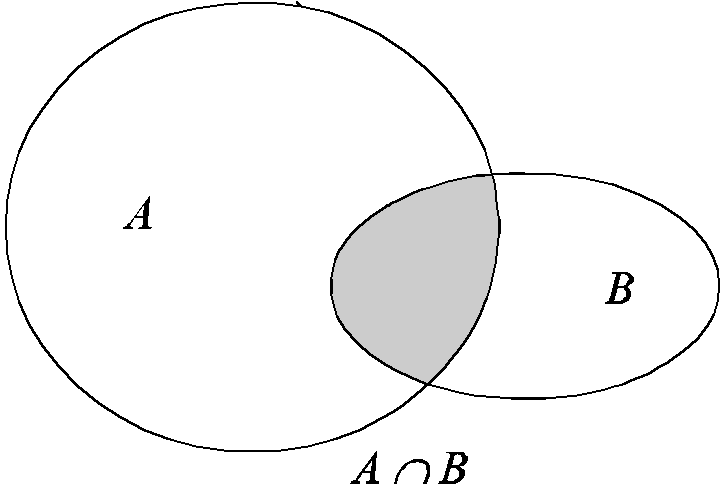
Если два множества не пересекаются. то это можно записать в виде AB=.

Объединение AB ={x:xA или xB}

Произведение множеств AB ={(x,y):xA и yB}.

Пример R² = R  R - плоскость.

2. Отображение, взаимно-однозначное соответствие, счетное и несчетные множества

Даны множества A и B. Отображение A в B (или функция определенная на A со значениями в B) - соответствие или закон (обозначим его f ), которое каждому a A сопоставляет единственное b  B, A B, f: A B, b = f(a).

a - прообраз, b - образ при отображении f.

Отображение из A в B называется взаимно-однозначным, если

1) разные элементы из A имеют разные образы

2) каждый элемент из B является образом некоторого элемента из A

Эквивалентные множества A  B или множества одинаковой мощности, если существует взаимно-однозначное соответствие между элементами этих множеств.

Счетное множество A  N

Пример: Множество рациональных чисел счетно.

Одно из важных свойств счетных множеств:

Объединение конечного или счетного числа счетных множеств является счетным множеством.

Несчетные множества

Бесконечное множество, не являющееся счетным, называется несчетным. Множество [0,1] имеет большую мощность, чем N. Множество эквивалентные по мощности отрезку [0,1] называются множествами мощности континуума. Множество действительных чисел R - несчетное множество, это множество является множеством мощности континуума.

3. Некоторые понятия математической логики (Дж. Маллас Пролог)

При описании логики Аристотеля употребляется понятие суждение. Суждение представляет собой законченную мысль, выраженную средствами естественного языка и (согласно Аристотелю) состоит из четырех элементов: квантор, субъект, связка, предикат.

Примеры:

	Квантор	Субъект	Связка	Предикат
1	Все	числа	являются	не рациональными
2	Некоторые	натуральные числа	-	четны

В последнем случае подразумевается связка “являются”. В первом случае обычно говорят также: “Все числа не являются рациональными”. Вместо термина предикат мы будем использовать также термин свойство. Противоположное свойство P или отрицание свойства P обозначается значком или .

В традиционной логике допускаются два типа суждений, каждый из которых характеризует возможные отношения между двумя классами (классом субъектов и классом предикатов):

Все S являются P ( каждый из S удовлетворяет свойству P )

Некоторые из S являются P ( существует представитель из S, удовлетворяющий свойству P )

Здесь S обозначает класс субъектов, а P - класс предикатов ( или некоторое свойство, характеризующее этот класс ). Все, каждый, любой, произвольный называются универсальным квантором или квантором общности. Квантор общности обозначается значком . Некоторые из, существует - экзистенциальные кванторы. Квантор существования обозначается значком . Таким образом, основные типы суждений можно записать в следующей форме ( логической связке соответствует символ двоеточия ):

1. xS:P

2. xS:P

Предикат и субъект в суждении могут быть составными, в частности они сами могут быть суждениями. Например, рассмотрим высказывание (суждение):

>0 >0 x,|x-x₀|< : |f(x)-2|<.

Это высказывание следует читать так: Для любого эпсилон больше нуля существует дельта больше нуля, (что) для всех икс, удовлетворяющих неравенству …, выполнено неравенство …. Это суждение является составным и может быть разложено на простейшие суждения следующим образом:

S₁ : P₁, где S₁-класс субъектов, S₁={xR,x>0}, P₁ - предикат,

P₁=(S₂ : P₂), где S₂=S₁, P₂ - предикат,

P₂=(xS₃: P₃), S₃= S₃()={xR:|x-x₀|<}, P₃ – предикат (свойство) |f(x)-2|<.

Прямая и обратная теоремы, эквивалентность, метод математической индукции

Структура простейшей теоремы выглядит следующем образом: дано свойство A (условие) , из него выводится свойство B (заключение).

В этом случае говорят A влечет B (A из следует B) и пишут A B . Последняя запись подразумевает, на самом деле, истинность выражения A B.

Если к тому же B A, то говорят, что верна и обратная теорема и пишут A B, при этом A и B называются эквивалентными.

Теорема. Отрицание суждения должно строиться по следующим формальным правилам:

1. квантор  заменяется на квантор 

2. квантор  заменяется на квантор 

3. предикат P заменяется на свое отрицание.

Пример:

>0 >0 x,|x-x₀|< : |f(x)-2|<.

его отрицание

>0 >0 x,|x-x₀|< : |f(x)-2|.

Доказательство достаточно провести для двух типов простейших суждений:

1.  x: P

2.  x: P.

Для таких суждений сформулированная теорема достаточно очевидна.

Метод математической индукции

Имеется последовательность свойств P_n. Если доказано свойство P₁ и

P_k P_k+1, то P_n справедливы для nN.