Конспект лекций Логинов А.С. ЭТФ 1 семестр loginov_1999@mail.ru

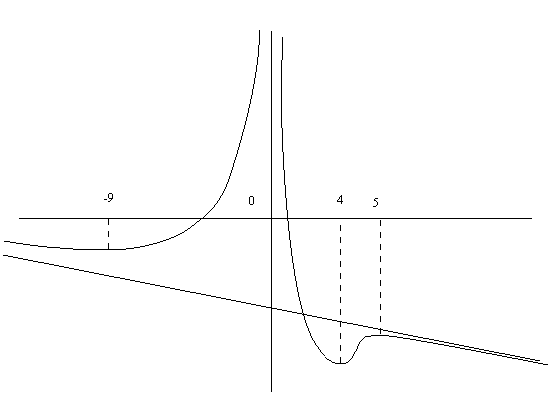
Пример.

Асимптоты ,x

Особые точки -9,0,4,5

	(-,-9)	-9	(-9,0)	0	(0,4)	4	(4,5)	5	(5,)
y	-	0	+		-	0	+	0	-
y									
y	+ 		+ 		+ 		+- 		- 

Пример

t	(-,-1)	-1	(-1,1)	1	(1,)
	+		+		-
x	-  -3	-3	-3  1	1	1  -
Диапазон x	(-,-3)		(-3,1)		(-,1)
dy/dx	-	0	+	3	+
y(x)	-2	-2	-22	2	-2
d2y/dx2	+		+		-

Пример.

. Асимптота y=2x при t+ (x+).

t	(-,0)	0	(0,+)
	-		+
x	+  1	1	1  +
Диапазон x	(1,+ )		(1,+ )
dy/dx	+	4	+
y	1	1	1
y	+		-

Построение графиков функций, заданных в полярной системе координат.

 : r = r(),[₁,₂].

Связь декартовой и полярной систем координат

x = r cos ,

y = r sin .

Параметризация кривой 

x = r() cos ,

y = r() sin  , [₁,₂].

Пример. Исследовать поведение кардиоиды r = 2(1 + cos t) в окрестности точек t = 0, t =  .

Задача для самостоятельного решения. На основании уравнения кардиоиды придумать параметрическое задание кривой, график которой показан на нижеследующем рисунке.

Ответ в конце документа.

Глава 5. Элементы теории кривых

§1 Векторная функция скалярного аргумента

1.Определение векторной функции. Операции над векторными функциями

На плоскости

, r(t)=x(t)i+y(t)j .

В пространстве

,r(t)=x(t)i+y(t)j+y(t)k .

Операции над вектор функциями

1) p(t), q(t)p(t)+ q(t)

2) (t)r(t)

3) Скалярное произведение ( p(t) , q(t) )

4) В трехмерном пространстве определено векторное произведение [ p(t) , q(t) ]

2. Предел вектор функции

Определение

r(t)=a=0

Или, что тоже самое |r(t) – a|=0 .

Замечание 1. Это определение не зависит от выбора базиса i , j , k.

Геометрическая интерпретация.

Теорема. (Критерий существования предела вектор функции) Для существования предела r(t) = a необходимо и достаточно существования пределов координат вектор функции. ие

r(t) = a

Доказательство. Для заданного значения параметра t максимум из трех чисел |x(t)-a_x|,| y(t)-a_y |,| z(t)-a_z | обозначим (t) = max{|x(t)-a_x|,| y(t)-a_y |,| z(t)-a_z |}. Для любого t справедливо неравенство

(t)  =|r(t) – a|.

С другой стороны |r(t) – a|= (t).

Из этих неравенств и следует требуемое утверждение.

Замечание 3. Для существования предела необходимо требовать, чтобы r(t) была определена в некоторой проколотой окрестности точки t₀.

Из теорем о пределах функций, с помощью доказанного критерия, получаются соответствующие теоремы для пределов вектор функций. Перечислим некоторые из них.

1. Предел, если он существует, единственен.

2. Предел суммы и произведения на обычную функцию

( p(t)+q(t) )=p(t)+q(t)

((t) p(t) )=(t)p(t)

3) ( p(t) , q(t) )=( a , b )

a=p(t) , b = q(t)

4) [ p(t) , q(t)]=[ a , b ]

3. Непрерывность вектор функции

r(t) определена на [,] и t₀(,)

r(t) непрерывна, если r(t) = r(t₀)

Аналогично определяется непрерывность справа, слева.

Непрерывность на множестве.

Свойства

p(t) , q(t) , (t) непрерывны в точке t₀  непрерывны p(t) + q(t), (t)p(t) ,( p(t), q(t)),

[ p(t) , q(t)]

4. Дифференцируемость вектор функции

Пусть r(t) определена в окрестности точки t₀.

Производной в точке t₀ называется нижеследующий предел, если он существует,

r(t)=(r(t) – r(t₀))/(t – t₀)

Теорема. Производная вектор функции r(t) в точке t₀ существует тогда и только тогда, когда существуют x(t₀), y(t₀), z(t₀) и r(t₀)=.

Утверждение следует из критерия существования предела вектор функции.

Замечание. Если у r(t) существует r(t₀) в точке t₀, то r(t) непрерывна в этой точке.

Определение. Векторная функция r(t) называется дифференцируемой в точке t₀, если в некоторой окрестности этой точки выполняется равенство

r(t) - r(t₀) =a(t – t₀) +(t) (t – t₀) (1)

где (t) = 0

Векторная функция a t = a (t – t₀) = a dt называется дифференциалом функции r(t) в точке t₀ и обозначается dr = a dt .

Условие (1) можно записать в координатной форме

(2)

гдеa=(a_x, a_y, a_z),  = (_x , _y , _z )

Теорема. Дифференцируемость r(t) в точке t₀ эквивалентна дифференцируемости в точке t₀ координат функции r(t).

Следствие. Для дифференцируемости r(t) в точке t₀ необходимо и достаточно существование r(t₀).

Геометрический смысл производной

r(t):

5. Правила дифференцирования вектор функций

1) ( r) = r +  r

2) (r₁ + r₂ ) = (r₁ + r₂ )

3) (r₁ , r₂ ) = (r₁ , r₂ ) + (r₁ , r₂ )

4) [r₁ , r₂ ] = [r₁ , r₂ ] + [r₁ , r₂ ]