Математический анализ 1 семестр / ma / matan_3

Конспект лекций Логинов А.С. ЭТФ 1 семестр loginov_1999@mail.ru

5. Критерий Коши существования предела функции

Пусть X область определения функции f содержит проколотую окрестность точки a .

Условие Коши для f(x) в окрестности a:

>0 x,xX:|f(x) - f(x)|<

Сформулируем условие Коши для других случаев

Односторонние пределы:

Предел справа >0>0x,x(a,a+)X:|f(x)-f(x)|<

Предел слева >0>0x,x( a-, a)X:|f(x)-f(x)|<

Условие Коши для +: f определена в окрестности +

>0bx,x(b,+)X:|f(x) - f(x)|<.

Условие Коши для -: f определена в окрестности -

>0ax,x(-,a)X:|f(x) - f(x)|<.

Условие Коши для : f определена в окрестности 

>0ax,x(-,a) (,a)X:|f(x) - f(x)|<.

Теорема. (Критерий Коши) Для существования конечного предела , где a число или символ н. и д., чтобы f удовлетворяла условию Коши в окрестности a.

Необходимость. Пусть >0, для /2  xX:|f(x)-A|</2. Для x,xX получим требуемое неравенство |f(x) - f(x)|<|f(x) - A|+|f(x) -A| < /2+/2=.

Достаточность. Пусть >0. Тогда  x,xX:|f(x)-f(x)|< . Если {x_n} последовательность типа Гейне для a , то из сходимости {x_n}a и условия x_na следует, что  Nn>N, p:x_nи x_n+p. Тогда для тех же n>N, p : |f(x_n) - f(x_n+p)|< . Таким образом, последовательность {f(x_n)} будет удовлетворять условию Коши для последовательностей, поэтому существует некоторый предел . Докажем, что для любой другой последовательности типа Гейне {y_n} предел будет также равен B. Составим последовательность

, {z_n}={x₁, y₁,x₂, y₂,x₃, y₃,…}.

Эта последовательность будет последовательностью типа Гейне при xa и, как уже доказано, предел должен существовать. Тогда все частичные пределы должны совпадать, в частности, =.

6. Локальная ограниченность функции, имеющей конечный предел

Область определения X функции f содержит некоторую проколотую окрестность .

Функция f локально ограничена в a (говорят так же «в окрестности a»), если она ограничена в некоторой окрестности этой точки. Для числа a определение локальной ограниченности выглядит следующим образом

M>0xU_(a)X:|f(x)|M.

Для a = + MbxU_b(+)X:|f(x)|M.

Теорема. Функция f(x) , имеющая конечный предел в при x a , локально ограничена в a.

Доказательство: =1, M=max{|A-1|,|A+1|,f(a)} или M=max{|A-1|,|A+1|} (последнее в случае, если функция не определена в a ).

Замечание. Теорема верна и в случае , .

7. Сохранение знака функции, имеющей ненулевой предел в точке

Область определения X функции f содержит некоторую .

Теорема.

( f(x) сохраняет знак A в некоторой окрестности a).

Доказательство. Для =.

Замечание 1.

Замечание 2. Теорема верна и в случае

8. Предел сложной функции

f(x) определена на X, g(t) определена на T с областью значений GX. Тогда на T определена суперпозиция F(t)=f(g(t)),tT. При этих условиях справедлива

Теорема. Пусть

g(t) определена на T= (,)\{t₀},t₀ (,).

f(x) определена на (a,b)\{x₀},

tT:g(t)x₀, если tt₀ ,

,

=A.

Тогда

Доказательство: Возьмем >0 для него >0x:f(x) U_(A), далее, для  существует >0t:g(t) , если tt₀ , то g(t)x₀. таким образом, g(t)и следовательно f[g(t)] U_(A).

§3 Свойства пределов

1.Переход к пределу в неравенствах

Т. Если f(x), g(x) определены на (a,b) за исключением быть может x₀(a,b) и f(x)g(x) на (a,b)\{ x₀} и существуют пределы, А и B числа, то AB.

Аналогично, для случая f(x)<g(x).

Т. Если f(x), g(x) определены на (a,b) за исключением быть может x₀(a,b) и f(x)< g(x) на (a,b)\{ x₀} и существуют пределы, А и B числа, то AB.

Эти утверждения следуют из соответствующих теорем о пределах последовательностей, используя определение предела по Гейне.

2. Арифметические операции над пределами

Везде в этом пункте рассматриваются конечные пределы.

1), , если .

2) , если существуют конечные пределы , .

3) , если существуют конечные пределы , .

Следствие: , если существует конечный предел .

4) 

5) g(x)0,, 

Замечание: Аналогичные свойства имеют место для односторонних пределов

3.Бесконечно малые и бесконечно большие функции

Опр. Бесконечно малой в x₀ называется функция f(x) такая, что

Свойства бесконечно малых функций

1) Критерий существования конечного предела функции

 б.м. функция (x) при xx₀ :f(x)=A+(x)

2) (x),(x) б.м.  (x)+(x) б.м.

3) Произведение б.м. функции на ограниченную является б.м. функцией.

4) Произведение б.м. функций является б.м. функцией.

Опр. f(x) определенная в проколотой окрестности x₀ называется бесконечно большой б.б. в т. x₀, если .

5) Если (x) б.м. при xx₀ и (x)0, то 1/(x) является б.б. и наоборот. Символически это записывают в виде 1/=0, 1/0= .

4. Сравнение б.м. и б.б. функций. Символы O,o

f,g определенны в некоторой проколотой окрестности x₀

Пишут, если

.

Аналогично определяется O при xx₀+0, xx₀ - 0, x, x .

Пример: f(x)=O(1),x означает локальную ограниченность функции в .

Опр. Если при xx₀ , f(x)=O (g) и g(x)=O (f) , то f(x), g(x) называются функциями одного порядка.

Пример: Функции x³,x² являются функциями одного порядка при x1.

Определение o. Пусть f(x), g(x) определенны в некоторой проколотой окрестности точки x₀, пишут f(x)=o(g(x)), xx₀, если

  б.м. (x) при xx₀ , такая, чтоx:f(x)=(x)g(x)

Аналогично определяется o при xx₀+0, xx₀ - 0, x, x.

Пример: f(x)=o (1), при xx₀ означает, что f(x) б.м. при xx₀ .

Некоторые примеры работы с символами o ( подразумевается x0 ).

o(xⁿ)  o(xⁿ)= o(xⁿ)

x^m o(xⁿ) = o(x^n+m)

c o(xⁿ) = o(xⁿ) (c-константа)

o(xⁿ)  o(x^n+p)= o(xⁿ), здесь p натуральное.

o(x^n+p)/x^p= o(xⁿ) В частности, o(x^p)/x^p= o(1).

o(a_n xⁿ a_n+1 xⁿ⁺¹… a_n+p x^n+p)= o(xⁿ)

Если , б.м. и =o(), то говорят, что  б.м. более высокого порядка, чем .

Определение. Функции f(x), g(x) называются эквивалентными в x₀ ( говорят так же, в окрестности x₀ ), если выполнено хотя бы одно из двух условий

f(x)=g(x)+o(g(x)), xx₀

g(x)=f(x)+o(f(x)), xx₀ .

Условие эквивалентности записывается в виде fg , при xx₀ .

Замечание 1. Если выполнено одно из этих условий, то будет выполнено и второе.

Замечание 2. Эти условия можно записать в другой форме. Например, первое из них: в некоторой проколотой окрестности точки имеет место равенство f(x)=h(x)g(x), =1.

Замечание 3. Если, например, g(x)0, то первое условие можно записать в виде .

Определение. Если f(x)  (x-x₀)ⁿ при xx₀ , то f(x) называется бесконечно малой порядка n при xx₀.

Если f(x)  при xx₀ , то f(x) называется бесконечно большой порядка n при xx₀.

Если f(x) б.б. при x и f(x) эквивалентна xⁿ при x , то f(x) называется бесконечно большой порядка n при x.

Замечание. Если f(x) б.м. порядка n, то 1/f(x) будет б.б. порядка n и наоборот.

Примеры. Определить характер функций , в 0, 1,+.

При вычислении пределов полезна следующая теорема

Т2. Пусть f эквивалентна f₁, g эквивалентна g₁ при xx₀ .

Если существует предел , тогда существует и .

Если существует предел , тогда существует и .

Опр. Если , то g называется главной частью f при x x₀.

§4 Замечательные пределы

1.

Для

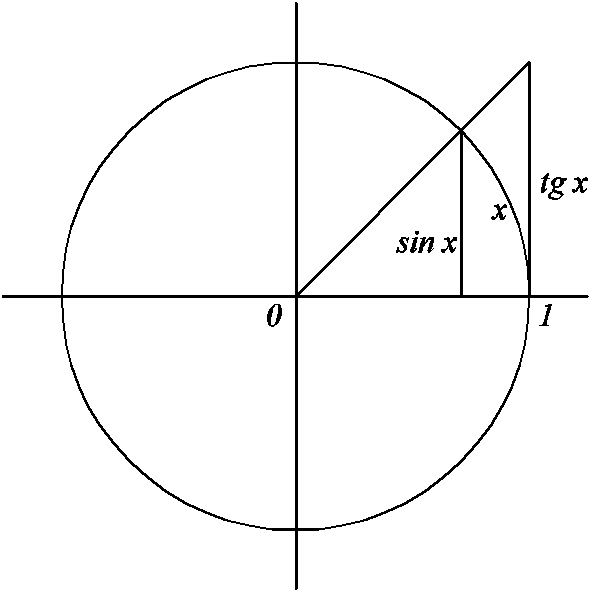
Откуда следуют неравенства

Далее cos x =1 и из (2)

Отметим, что было доказано:

2.

Лемма 1.x_n=a, {n_k} - последовательность натуральных чисел n_k=+ =a.

Доказательство:

N_n>N_ :|x_n - a|< (3)

Для N_ Kk >K: n_k>N_ из (3) следует |- a|<.

Лемма 2. Если x_k=0, x_k>0, то =e.

Доказательство: Будем считать, что x_k < 1. Для целой части числа , n_k= будут выполнены неравенства:

,

Поэтому

(4)

Пределы последовательностей , согласно лемме 1, равны числу e. Для того, чтобы это проверить, эти последовательности можно представить в виде:

.

Переходя к пределу в (4) при k по теореме о трех последовательностях получим требуемое утверждение .

Следствие 1. .

Действительно, утверждение леммы 2 означает, что для любой последовательности {x_k} типа Гейне при x0 будет выполнено =e.

Аналогичное утверждение справедливо для предела слева .

Следствие 2. ,. Первое утверждение следует из теоремы о связи предела с односторонними пределами. Последнее равенство получено с помощью замены x = 1/y.

Основные эквивалентности

sin x  x, x0,

a^x-1 x ln a, x0,

ln(1+x ) x, x0.

Второе и третье будет доказано в последующем.

32

Конспект лекций Логинов А.С. ЭТФ 1 семестр loginov_1999@mail.ru