
Шпоры по матану 2011-2012 / матан шпоры 9
.docxПроизводная и дифференциал функций, заданных параметрически.
Функцию
 можно задавать с помощью двух отображений
можно задавать с помощью двух отображений
 и
и
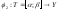 композицией
композицией
 Такую
функцию записывают в форме
Такую
функцию записывают в форме
 ,
,
 .
Существование
.
Существование
 может
обеспечить, например, строгая монотонность
функции
может
обеспечить, например, строгая монотонность
функции
 .
.
ПРИМЕР 1. Функция
 на
отрезке [-1; 1] может быть задана
параметрически:
на
отрезке [-1; 1] может быть задана
параметрически:
 ,
,
 .
Тогда
.
Тогда

 .
.
Теорема о дифференцируемости функции заданной параметрически
Пусть функция
 задана параметрически
задана параметрически
 ,
,
 ,
причем
,
причем
 - дифференцируемые на отрезке
- дифференцируемые на отрезке функции и
функции и
 .Тогда
в каждой точке x
, соответствующей
значению t
, т.е.
.Тогда
в каждой точке x
, соответствующей
значению t
, т.е.
 ,
существует производная
,
существует производная
 ,
равная
,
равная
 и дифференциал
и дифференциал .
.
ДОК. (1)
 .
.
(2)
 .
.
Локальный экстремум функции
ОПР.
Точка
 называется
точкой локального максимума функции
называется
точкой локального максимума функции ,
определенной в некоторой окрестности
,
определенной в некоторой окрестности
 ,
если
,
если
 .
Если неравенство строгое для всех
.
Если неравенство строгое для всех
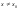 ,
то говорят о строгом локальном максимуме.
,
то говорят о строгом локальном максимуме.
ОПР. Точка
 называется
точкой локального минимума функции
называется
точкой локального минимума функции
 ,
определенной в некоторой окрестности
,
определенной в некоторой окрестности
 ,
если
,
если
 .
Если неравенство строгое для всех
.
Если неравенство строгое для всех
 ,
то говорят о строгом локальном минимуме.
Если функция имеет в точке
,
то говорят о строгом локальном минимуме.
Если функция имеет в точке
 локальный
минимум или локальный максимум, то
говорят о локальном экстремуме функции.
локальный
минимум или локальный максимум, то
говорят о локальном экстремуме функции.
ПРИМЕР 1.(не характерный)
Функция
 имеет, по определению, в точке
имеет, по определению, в точке
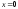 строгий локальный максимум, поскольку
строгий локальный максимум, поскольку
 ,
не смотря на то, что убывает в левосторонней
окрестности и возрастает в правосторонней
окрестности точки
,
не смотря на то, что убывает в левосторонней
окрестности и возрастает в правосторонней
окрестности точки
 .
Следующая теорема устанавливает
необходимые условия локального
экстремума.
.
Следующая теорема устанавливает
необходимые условия локального
экстремума.
Теорема Ферма
Если функция
 в точке
в точке
 имеет
локальный экстремум, то либо функция
не имеет производную в точке
имеет
локальный экстремум, то либо функция
не имеет производную в точке
 ,
либо эта производная равна нулю.
,
либо эта производная равна нулю.
ДОК. (1) Если
производной в точке
 нет,
то теорема доказана (см. пример 1). (2)
Пусть производная
нет,
то теорема доказана (см. пример 1). (2)
Пусть производная
 существует и
существует и
 .
Тогда
.
Тогда

и
знак
 для
достаточно малых
для
достаточно малых
 определяется знаком выражения
определяется знаком выражения
 ,
а он меняется в зависимости от знака
,
а он меняется в зависимости от знака
 .
Последнее противоречит условию
локального экстремума в точке
.
Последнее противоречит условию
локального экстремума в точке
 ,
т.е.
,
т.е.
 .
.
Теоремы о среднем для производных. Теорема Ролля
Если функция
 1) непрерывна на отрезке [a;b],
1) непрерывна на отрезке [a;b],
2) дифференцируема
в каждой точке интервала (a;b),
3) принимает на концах
отрезка равные значения :
 ,
,
то существует на
интервале (a;b)
такая точка c
, для которой
 .
.
ДОК. По доказанной
теореме непрерывная на [a;b]
функция принимает на этом отрезке
наибольшее и наименьшее значения :
 и
и
 .
Если одна из точек c1
или c2
лежит на интервале (a,b)
, то теорема доказана, поскольку эта
точка является точкой локального
экстремума и по теореме 1
.
Если одна из точек c1
или c2
лежит на интервале (a,b)
, то теорема доказана, поскольку эта
точка является точкой локального
экстремума и по теореме 1
 .
Если
.
Если
 или
или
 ,
но они совпадают с концами отрезка, то
,
но они совпадают с концами отрезка, то

 и
функция постоянная на отрезке[a;b]
и
и
функция постоянная на отрезке[a;b]
и
 .
.
ПРИМЕР 2 . Функция
 на отрезке
на отрезке
 удовлетворяет всем условиям теоремы
Ролля, кроме одного: в точке
удовлетворяет всем условиям теоремы
Ролля, кроме одного: в точке
 функция не имеет производную. При этом
утверждение теоремы не выполняется:
функция не имеет производную. При этом
утверждение теоремы не выполняется:
 для
для
 и
и
 для
для
 .
.
Теорема Коши
Если функции
 и
и
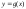 1) непрерывны на отрезке [a;b],
2) дифференцируемы в каждой точке
интервала (a;b),
3)
1) непрерывны на отрезке [a;b],
2) дифференцируемы в каждой точке
интервала (a;b),
3)
 на интервале
на интервале
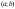 ,
,
то существует на интервале (a;b) такая точка c , для которой
 .
.
ДОК. Из условия
теоремы следует, что
 .
Действительно, если
.
Действительно, если
 ,
то функция
,
то функция
 удовлетворяет
условиям теоремы Ролля и тогда найдется
такая точка c
, для которой
удовлетворяет
условиям теоремы Ролля и тогда найдется
такая точка c
, для которой
 ,
что противоречит условию 3) теоремы.
Рассмотрим вспомогательную функцию
,
что противоречит условию 3) теоремы.
Рассмотрим вспомогательную функцию
 .
.
Проверим, что
 .
Действительно,
.
Действительно,

и
функция
 удовлетворяет
условию теоремы Ролля. Тогда найдется
удовлетворяет
условию теоремы Ролля. Тогда найдется
 ,
для которой
,
для которой
 .
.
Из последнего равенства следует утверждение теоремы.
Теорема Лагранжа
Если функции
 1) непрерывна на отрезке [a;b],
1) непрерывна на отрезке [a;b],
2) дифференцируема в каждой точке интервала (a;b), то существует на интервале (a;b) такая точка c , для которой
 .
.
ДОК. Следует из
теоремы Коши для
 .
.
Правило Лопиталя для раскрытия неопределенности 0/0
Если
функции
 и
и
 1) непрерывны на [a;b)
, ( а и b
не обязательно
конечны), 2) дифференцируемы в каждой
точке интервала (a;b),
3)
1) непрерывны на [a;b)
, ( а и b
не обязательно
конечны), 2) дифференцируемы в каждой
точке интервала (a;b),
3) на интервале
на интервале
 ,
,
4)
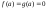 ,
5) существует
,
5) существует
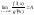
то
существует
 .
.
ДОК. Для любого
 на отрезке
на отрезке
 выполняются условия теоремы Коши и
найдется
выполняются условия теоремы Коши и
найдется
 ,
для которого
,
для которого
 .Если
.Если
 ,
то
,
то
 и
и

 =
= .
.
В теореме допускается
случай
 .
.
Правило Лопиталя
для раскрытия неопределенности

Если функции
 и
и
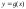 1) непрерывны на [a;b)
, ( а
и b
не обязательно
конечны), 2) дифференцируемы в каждой
точке интервала (a;b),
3)
1) непрерывны на [a;b)
, ( а
и b
не обязательно
конечны), 2) дифференцируемы в каждой
точке интервала (a;b),
3)
 на интервале
на интервале
 ,
,
4)
 ,
,
 ,5)
существует
,5)
существует
 .,
.,
то существует
 .
.
ДОК. (1) Пусть А –
конечное число. Тогда
 .
Определим функцию
.
Определим функцию
 из условия
из условия
 ,
т.е.
,
т.е.
 Заметим, что
Заметим, что
 .(условие
5)) Применим для отрезка
.(условие
5)) Применим для отрезка
 и
функций
и
функций
 теорему Коши. Тогда для некоторой точки
теорему Коши. Тогда для некоторой точки
 :
:

и
для всех x
, для которых
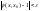 имеем
имеем

т.е. .
.
(2)
Пусть
 .
Тогда
.
Тогда
 .
.
Если x
достаточно
близок к a
, то из
 следует
следует
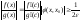 и
и
 .
.
