7. Базисное хеджирование фьючерсами на облигации

Фьючерсы на облигации используются для хеджирования портфелей облигаций. Кажется, что фьючерсные контракты нужно иметь на сумму, которая совпадает со стоимостью облигаций в портфеле. Если облигаций в портфеле 1 млн. $, то нужно иметь 10 фьючерсных контрактов на облигации Казначейства, каждый из которых на условную сумму 100’000$. Это вытекает из того простого обстоятельства, что дельта фьючерса равна единице (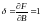 ), поскольку фьючерс – это линейный инструмент.

Однако при этом не учитывается разница между условной облигацией, которая лежит в основе фьючерса, и реальной облигацией, которая по этому фьючерсу может быть поставлена. Иными словами, фьючерсный контракт заключается на одну облигацию (эталонную), а поставляется какая-то другая облигация (самая дешевая для поставки). Поэтому дельта фьючерса для поставляемой облигации может быть и не равна единице. Найти дельту не сложно, учитывая, что она представляет собой первую производную фьючерса по базовому активу.

Из уравнения цены фьючерса видно, что малые изменения фьючерса при малых изменениях самой дешевой облигации, определяются по формуле:

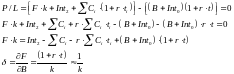
При малых промежутках времени t и малых безрисковых ставках процента можно принять, что .

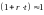Следовательно, чувствительность фьючерсов к изменениям цен спот обратно пропорциональна величине переводного множителя.

Таким образом, из разложения в ряд Тейлора с учетом только его первого члена получаем:

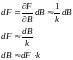
Следовательно, если k = 1.2 и цена облигации dB изменилась бы на 6 bp, то цена фьючерса изменилась бы на 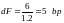. Значит, фьючерс изменился бы на меньшую величину, чем изменилась цена облигации. Стало быть, чтобы защитить такую облигации нужно больше фьючерсов. Насколько больше? На величину переводного множителя. Тогда цена фьючерса изменится на 5 bp, а всего фьючерсов будет k=1.2. Следовательно, общая позиция изменится на 5∙1.2=6 bp, т.е. ровно на столько, на сколько изменилась цена облигации.

Оказывается, если нужно защитить самые дешевые для поставки облигации, необходимо иметь в k раз больше фьючерсных контрактов. Если k>1, то потребуется больше фьючерсов для компенсации изменений спот позиции; если k<1, то потребуется меньше фьючерсов.

Таким образом, если инвестор имеет портфель облигаций из предыдущего примера (с=9.25%, T=23 года, k=1.1296) на 10 млн. $ (занимает длинную позицию на рынке спот), то для защиты портфеля ему нужно продать (занять короткую позицию) 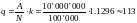фьючерсных контрактов.

Эффективность хеджирования определяется по формуле:

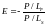
где P/L_F – это P/L по фьючерсной позиции;

P/L_S – это P/L по позиции спот.

Знак минус появляется потому, что позиции на фьючерсом рынке и на рынке спот движутся в противоположном направлении.

1 Society of Actuaries Professional Actuarial Specialty Guide Asset-Liability Management. - Финансы/Инжиниринг/Риски/ALM/spg0308alm, с.1(6)

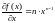
2 Macaulay, Frederic. Some Theoretical Problems Suggested by the Movements of Interest Rates, Bond Yields, and Stock Prices in the U.S. Since 1856. National Bureau of Economic Research: New York, 1938

3 Функция f(x)=xⁿ. Ее производная равна: .

4 http://www.cbot.com/cbot/pub/cont_detail/0,3206,1526+702,00.html