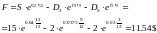- •Принятие решений в условиях неопределенности
- •Этапы развития риск-менеджмента
- •Риск и возможности
- •Риск и цели
- •Риск и свобода
- •Риск и неопределенность
- •Риск и затраты
- •Принятие решений
- •Риск и вероятность
- •Принципы управления риском
- •Идентификация рисков
- •Виды рисков
- •Факторы, характеризующие риск
- •Оценка риска
- •Меры без учета вероятностей
- •Меры с учетом вероятностей
- •Стратегия управления риском
- •Страхование
- •Диверсификация
- •Согласование активов и пассивов
- •Хеджирование
- •Чувствительность к изменению ставок процента
- •Оценка чувствительности
- •Формулы дюрации (Duration)
- •Дюрация долларовая
- •Дюрация модифицированная
- •Пример 2. Процентное изменение цены облигации с использованием модифицированной дюрации
- •Дюрация Маколи (Macaulay)
- •Пример 4. Дюрация Маколи
- •Формулы выпуклости (Convexity)
- •Пример 5. Изменение цены облигации с использованием дюрации и выпуклости
- •Мэтчинг дюраций
- •Хеджирование
- •Фьючерсы
- •Ценообразование фьючерсных контрактов
- •Деривативы на Price-Discovery Markets (ценораскрывающий рынок)
- •Деривативы на рынке «плати и забирай».
- •Конверсионные уравнения (b,s,f)-рынка
- •Состав справедливой цены
- •Форвардный кэш и форвардный кредит
- •Ценообразование активов при форвардом кэше
- •Фьючерсы на акции
- •Фьючерсы на акции без дивидендов
- •Фьючерсы на акции с дивидендами
- •Фьючерсная цена на акции с известными дивидендами
- •Фьючерсная цена на акции с постоянной дивидендной доходностью
- •Индексные фьючерсы
- •Индексы и особенности их расчета
- •Стоимость индексного фьючерса
- •Справедливая цена индексного фьючерса
- •Коэффициент хеджирования
- •Товарные фьючерсы
- •Фьючерсы на инвестиционные товары
- •Фьючерсы на не инвестиционные товары
- •Валютные фьючерсы
- •Фьючерсы на облигации
- •Справедливая цена облигации
- •Переводной множитель
- •Арбитражные стратегии
- •Самая дешевая для поставки облигация
- •Обусловленная ставка repo
- •Опционы продавца
- •Базисное хеджирование фьючерсами на облигации
Фьючерсы на акции с дивидендами
Фьючерсная цена на акции с известными дивидендами
Если по акции выплачиваются дивиденды, то ее форвардная цена определяется по формуле:
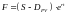
F – форвардная цена;
S – цена спот;
DPV – дисконтированная стоимость дивидендов.
Любая другая цена приводит к появлению арбитражных возможностей.
Если F > (S – DPV)∙ert, то продаем дорогой F и, значит действуем по схеме S – B - F. Иными словами: покупаем акцию (+S), продаем облигацию (-B) и продаем фьючерс (-F). Стало быть, сформируем портфель следующим образом:
Возьмем кредит в банке в размере S (-B);
Купим на эту сумму акцию (+S);
Займем короткую позицию по акции (примем на себя обязательство продать акцию в будущем по цене F) (-F).
(Продаем дорогую будущую акцию и покупаем дешевую сегодняшнюю акцию, а средства для покупки берем от продажи дисконтных облигаций в размере b∙z.)
Позиция на (B,S) рынке: S – B - F > 0
В момент поставки акции мы получим следующие денежные потоки:
Доход от продажи акции в размере F;
Дивиденды в размере D∙ert;
Расход – погашение кредита – в размере S∙ert.
Чистый доход, или P/L по сделке: (F +D∙ert) - S∙ert =F +(D – S)∙ert > 0.
Поскольку имеется возможность получить деньги без всякого риска и без начальных вложений собственных средств, то эта операция будет пользоваться популярностью у множества финансовых институтов. Спрос на акции возрастет, и цена акции S вырастет. С другой стороны, будущие продажи акции возрастут и, следовательно, ее форвардная цена F снизится. Это базовый алгоритм действий рационального инвестора.
Если же, напротив, F < (S - D)∙ert, то сформируем следующий портфель:
Занимаем у брокера акции S и продаем их (осуществляем короткую продажу);
Полученную сумму в размере S размещаем в банк под ставку r;
Занимаем длинную позицию по акции (принимаем на себя обязательство купить акцию в будущем по цене F).
Позиция на (B,S) рынке: S – B - F < 0
В момент будущей покупки акции получаем следующие денежные потоки:
Доход – сумма депозита в размере S∙ert;
Расход – упущенные дивиденды (дивиденды компенсируемые брокеру) в размере D∙ert;
Расход – покупка акции по цене F.
Купленную акцию возвращаем брокеру. Чистый доход от операции, или P/L по сделке равен: S∙ert - D∙ert - F = (S - D)∙ert - F > 0.
Опять-таки возможность получения дохода без вложения собственных средств и без всякого риска привлечет внимание арбитражеров. Поэтому текущие продажи акций увеличатся и их цена спот – S – упадет. С другой стороны, будущая цена акции – F – возрастет, поскольку их будут больше покупать. Через некоторое время цены установятся таким образом, чтобы исключить любые арбитражные возможности.
Поэтому единственной экономически обоснованной форвардной ценой акции будет цена F = (S - D)∙ert.
Пример 8. Форвардная цена акции с выплатой дивидендов в момент покупки
Тогда
|
Пример 9. Форвардная цена акции с дивидендами, выплачиваемыми в течение срока владения 1
Тогда
|
Можно определить форвардную цену акции, если дивиденды не дисконтировать, а, напротив, найти их FV (future value). Тогда эти дивиденды мы будем вычитать из FV акции, т.е. из ее форвардной цены без дивидендов. Причем в этом случае мы не знаем, какие ставки будут действовать через 3 месяца на 9 месяцев и через 9 месяцев на три месяца. Поэтому придется пользоваться не ставками спот, а ставками форвард.
Пример 10. Форвардная цена акции с дивидендами, выплачиваемыми в течение срока владения 2
Тогда
|

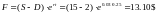
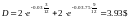 - дисконтированная сумма дивидендов.
- дисконтированная сумма дивидендов.