1. Фьючерсы

Фьючерс – это стандартный биржевой контракт, в соответствии с которым стороны несут обязательство купить или продать товар в будущем по заранее оговоренной цене. Покупатель находится в длинной позиции, а продавец – в короткой.

В соответствии с современной теорией фьючерсные цены информационно эффективны. Это означает, что фьючерсные цены – это несмещенные оценки будущих спотовых цен и эффективные индикаторы подлинной стоимости при условии, что известна вся информация, влияющая на спрос и предложение. Поэтому фьючерсные цены товара и цены товара спот изменяются синхронно. Это позволяет хеджировать ценовой риск.

Прибыль по фьючерсу на момент исполнения (FV):

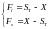
где:

T – срок истечения контракта;

Х – цена исполнения;

F_l – прибыль по длинной позиции;

F_s – прибыль по короткой позиции

Рисунок 6. Зависимость цены дериватива от цены базового актива

Разница между ценой фьючерс и ценой спот называется базис.

b = F – S

где b – базис, F – фьючерс, S – цена спот. На момент поставки базис равен нулю, поскольку цена фьючерса совпадает с ценой спот. Цена фьючерса зависит от цены базового актива.

Рисунок 7. Цена форвард цена спот и базис

По мере продвижения к дате погашения базис сужается, поскольку на момент исполнения он равен нулю.

Цены фьючерсов с разными сроками исполнения изменяются синхронно, поскольку в их основе лежит одинаковая цена спот.

Для обеспечения гарантии выполнения сделки обе стороны контракта вносят гарантийный задаток – маржу. Маржа обычно составляет от 2% до 10% от стоимости контракта. В Европе принята система постоянной корректировки маржинального счета, а в США маржа обычно делится на постоянную и переменную. Поэтому корректировка происходит только тогда, когда убыток превышает переменную маржу. Это резко снижает потоки платежей и сокращает организационные расходы.

Расчет по фьючерсу ежедневный. Дата погашения не влияет на величину прибылей или убытков. Такая особенность фьючерсов приводит к тому, что компания обменивает ценовой риск на риск ликвидности. Хотя цена продукта оказывается предсказуемой, но непредсказуемыми оказываются притоки и оттоки по фьючерсным позициям.

2. Ценообразование фьючерсных контрактов

Казалось бы, что цена форварда – это будущая, прогнозируемая сейчас цена спот. При прогнозировании нужно будет только сделать поправки на время и на неопределенность. Однако это не совсем верно и в основе ценообразования форвардов лежит другая технология. Более того, будущая цена спот практически никогда не совпадает с ценой исполнения форварда. Поэтому нельзя путать будущую (фьючерсную) цену спот и цену фьючерса.

Фьючерсная (будущая) цена устанавливается на основе рыночных ожиданий, а цена фьючерса (инструмента) устанавливается на основе арбитража.

1. Деривативы на Price-Discovery Markets (ценораскрывающий рынок)

Некоторые рынки имеют такие базовые активы, которые не могут быть приобретены и храниться до исполнения контракта. Возможно, что по ним нет рынка спот, как, например, по контрактам на весеннюю пшеницу. Когда они заключаются, спот рынка еще нет.

Поскольку в данном случае стратегия занять-купить-хранить неприменима, то любая информация о будущем спросе/предложении базовых товаров не может повлиять на соответствующей рынок спот. Однако такая информация может быть (в соответствии с терминологией) раскрыта на фьючерсном рынке.

Отношение между фьючерсной F(t) и спот ценой S_t точно известно только на дату исполнения T. В случае форвардов или фьючерсов

F(T)=S_T

В остальное время (t<T) фьючерсная цена F(t) может быть не равна спотовой S_t. Однако и в этом случае можно определить функцию, которая связывает цену спот S_t с ценой фьючерс F(t).

Предположим, что мы имеем форвардный контракт на акцию. Нужно определить: сколько будет стоить этот контракт сейчас?

Стоимость контракта в будущем (S_T - K), где S_T – цена акции через год, K – цена, по которой акция будет куплена/продана.

Текущая стоимость этого контракта

Цена акции S в будущем неизвестна и является случайной переменной, поэтому следует воспользоваться оператором матожидания.

При эффективном рынке цена контракта на момент исполнения должна быть равна нулю

так как в противном случае какая-то сторона получает выгоду.

F = F_L + F_S = S - K + K - S = 0

Но это означает, что

Что такое это матожидание? Поскольку

то

где Х нормально распределена.

Неизвестной величиной является степень числа е. Переменная, которая характеризует степень, распределена нормально.

Нормально распределенная величина имеет функцию плотности вероятности

Цены активов – S – не распределены нормально, но их доходности распределены логнормально. Движение доходностей активов моделируется геометрическим броуновским движением, или процессом Ито:

А движение логарифмов цен активов – арифметическим броуновским движением

Переход между двумя этими процессами осуществляется с помощью формул

Можно записать, что

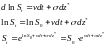
Но отсюда отнюдь не следует, что ожидаемым значением S_t является .

На самом деле ожидаемая цена акции будет

Поскольку случайная переменная dz распределена нормально с нулевым средним, то ее ожидаемое значение равно нулю.

Этот подход дает возможность определить цену форвардного контракта.

Подобная техника работает не только для форвардных контрактов. Дисконтируя ожидания, можно сравнивать полученные значения с теми, которые сложились на рынке.