Пример 4. Дюрация Маколи

Продолжим предыдущий пример. Дюрация Маколи: Таким образом, дюрация нашей облигации: 4.253 года.

Дюрация Маколи позволяет разграничить физическое и экономическое время жизни актива. Облигация со сроком погашения 5 лет имеет реальный срок жизни как актива – 4.253 года. Чем больший срок физической жизни у облигации, тем большую долю приносимого ей дохода «съедают» альтернативные издержки.

Дюрация купонной облигации – это (примерно) срок эквивалентной по доходу дисконтной облигации (с нулевым купоном). Поэтому для дисконтных облигаций срок погашения и дюрация совпадают. Для дисконтных облигаций имеется только один денежный поток, естественно, что он обладает единичным весом.

Возьмем для примера облигацию со следующими параметрами:

1. T=5 лет;

2. N=1000$;

3. с=10%;

4. r=5%.

Ее дюрация, как мы знаем, равна δ_M = 4.253 года. Возьмем другую, дисконтную облигацию с такими же номинальными выплатами, как и купонная облигация. Предположим, что дисконтная облигация принесет однократный платеж, равный1500$, через 4.253 года. Это такие же выплаты, как и по пятилетней облигации (500$ купонные выплаты и 1000 номинал). Какова должна быть справедливая стоимость этой облигации?

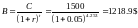
Это близко к справедливой цене купонной облигации, которая составляет 1216.47$.

Если мы знаем справедливую стоимость купонной облигации, то ее дюрацию можно найти по соответствующей дисконтной облигации:

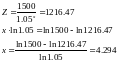
Поскольку для дисконтных облигаций дюрация Маколи совпадает с их сроком погашения, то дисконтные облигации обладают очень высокой чувствительностью к ставкам процента, т.е. подвержены очень высокому процентному риску. Например, для 50-летней дисконтной облигации при доходности r=5%, дюрация Маколи равна δ_M=50, а модифицированная дюрация – δ=47.62. Это означает, что при повышении требуемой доходности на 1% (с 5% до 6%) цена такой дисконтной облигации упадет на 47.62%.

Дюрация сводит в один показатель две зависимости:

1. чем больше срок облигации, тем больше дюрация (больше чувствительность к ставке процента);

2. чем больше купон, тем меньше дюрация (меньше чувствительность к ставке процента).

Комплексный показатель чувствительности – это и есть дюрация.

Следовательно, дюрация – это:

1. Дюрация долларовая – это наклон касательной к графику PV (в долларах);

2. Дюрация Маколи – это средний промежуток времени до момента погашения, взвешенный по объемам выплат (в годах).

3. Дюрация модифицированная – это эластичность цены по ставке процента;

4. Формулы выпуклости (Convexity)

Выпуклость (долларовая) – это вторая производная цены облигации по доходности.

Функция может быть разложена в ряд Тейлора:

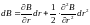
Вторая производная цены облигации называется выпуклостью в денежном выражении, поскольку измеряется в деньгах (например, долл. – долларовая выпуклость):

Разделим все на B

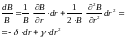
Просто выпуклость, как безразмерный коэффициент:

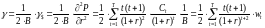
Следовательно, для прогнозирования процентного изменения цен облигаций в связи с ожидаемыми изменениями ставки процента, рассчитывается модифицированная дюрация (δ) и выпуклость (γ).

Аппроксимация изменения цены облигации в денежном выражении предполагает использование долларовой дюрации и долларовой выпуклости, т.е. первой и второй производной:

или

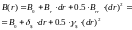
Это уравнение:

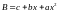
т.е. это уравнение параболы. Парабола более точно описывает выпуклую функцию.

Если ограничиться только первой производной (дюрацией), то уравнение:

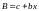
т.е. это уравнение прямой.

Аппроксимация изменения цены облигации в относительных величинах (процентной доходности) требует использования модифицированной дюрации и обычной выпуклости:

Выпуклость облигации всегда положительна. Выпуклость измеряет скорость изменения наклона кривой (ускорение), а этот наклон становится менее крутым по мере роста доходности. При малых доходностях крутизна PV очень велика, а при больших доходностях PV все больше приближается к прямой. Следовательно, с ростом доходности касательная к графику PV будет поворачиваться против часовой стрелки. Чем быстрее она будет поворачиваться, тем выпуклость выше.

Для положительной дюрации инструмента без встроенных опционов положительная выпуклость означает, что дюрация увеличивается при падении ставки процента, и дюрация сокращается, когда ставки процента растут. Все облигации с фиксированным купоном имеют положительную дюрацию и положительную выпуклость.

Таким образом, дюрация – это скорость изменения цены облигации при изменении доходности, а выпуклость – ускорение.