1. Прикладные задачи как источник основных представлений теории обыкновенных

дифференциальных уравнений.

1.Принципы составления дифференциальных уравнений.

Для составления и интегрирования дифференциальных уравнений приводят различные задачи физики, биологии, химии и т.д.

Например, при решении задач искомая кривая представляется как график некоторой функции, как y=y(x)

Все связные (названные) в задачах величины, выражаются через аргумент x, функцию y и её производную: .

Полученное при таком условии соотношение и представляет собой дифференциальное уравнение.

Уравнение (1) является искомым уравнением для нахождения неизвестной функции у.

При решении физических задач процесс составления дифф. Уравнения разбивается на 3 этапа:

1)одну из величин выбираем в качестве независимой переменной 2-го в качестве зависимой переменной. Чаще всего в качестве независимой переменной выбираются время t, а в качестве искомых функций пространственные координаты x,y,z.

2)находим на сколько измениться искомая функция Х, если независимая переменная t получит достаточно малое приращение

, то есть пытаемся оценить разность ч/з величины, данные в задачи.

3)делим полученное неравенство на и переходим к lim, когда в результате предельного перехода получаем дифф. Уравнение из которого можно найти искомую функцию.

1.Принципы составления дифференциальных уравнений.

Для составления и интегрирования дифференциальных уравнений приводят различные задачи физики, биологии, химии и т.д.

Например, при решении задач искомая кривая представляется как график некоторой функции, как y=y(x)

Все связные (названные) в задачах величины, выражаются через аргумент x, функцию y и её производную: .

Полученное при таком условии соотношение и представляет собой дифференциальное уравнение.

Уравнение (1) является искомым уравнением для нахождения неизвестной функции у.

При решении физических задач процесс составления дифф. Уравнения разбивается на 3 этапа:

1)одну из величин выбираем в качестве независимой переменной 2-го в качестве зависимой переменной. Чаще всего в качестве независимой переменной выбираются время t, а в качестве искомых функций пространственные координаты x,y,z.

2)находим на сколько измениться искомая функция Х, если независимая переменная t получит достаточно малое приращение

, то есть пытаемся оценить разность ч/з величины, данные в задачи.

3)Делим полученное неравенство на и переходим к lim, когда в результате предельного перехода получаем дифф. Уравнение из которого можно найти искомую функцию.

.

2. Уравнения, разрешенные относительно производной.

Дифф. уравнением наз. равенство, связывающее независимую переменную x и зависимую переменную y с её производной.

Порядок самой старшей производной входящей в задание этого уравнения наз.порядком этого уравнения.

Рассмотрим обыкновенные дифф.уравнения 1-го порядка вида (1):

где F-заданная функция аргументов, F может определить не при всех значениях своих аргументов. Поэтому будем говорить об области определения функции F, D как область задания уравнения (1)’.

Иногда (1)’ удаётся выразить производную y’ через независимую переменную x и зависимую переменную y, то есть получим уравнение вида:

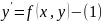
Это также уравнение первого порядка (обыкновенное) уравнение (1) называется уравнением относительно производной.

Уравнение (1)’ –уравнение не разрешено относительно системы производной.

Решением уравнения (1)’ будем называть всякую функцию y=y(x) определена на числовом промежутке которые при постановке в уравнении (1)’ обращает его тождество на интервале промежутка .

Промежуток наз.промежутком опред.решения y(x).

Следует отличить, что подстановка функции y в (1)’ возможна в том случае, если, когда y(x) имеет первую производную на всем интервале, а также при .

Для описания геометрического смысла решения уравнения разрешенной относительно производной (1) рассмотрим координатную плоскость Oxy.

Функция f может быть определена не во всей плоскости Oxy, а только в некоторой её части – области D.

Относительно D будем считать, что это открытая область, на которой сама функция f и её частное 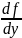непрерывны тогда решение y=y(x) в области D опред.некоторую кривую.

РИСУНОК!!!

Эта кривая в каждой точке области D имеет касательную ; tg угла которой равен значению f в этой точке, значит данная кривая является гладкой.

Эта кривая целиком лежащая в области D называется кривой дифф.уравнения(1).

Другими словами интегральная кривая – это график решения; для выделения из всего множества уравнения (1) того решения, которое описывает наблюдаемый процесс, вводят дополнительные условие; требуют, чтобы функция в точке x₀ принимала значение y₀.

Дифф уравнение (1) опред значение производной y’ в любой точке с координат (x,y) в области Д, а значит опр знач условия координатной касательной к интегральной кривой, т.е. направление движения по интегральной прямой.

РИСУНОК

То есть уравнение (1) опред поле направления касательных.

Геометрически задача интегрирования уравнения (1) сводится к поиску интегральной кривой, направление касательных к которым в каждой точке совпадают с направлением поля.

Изоклиной называют геометрическое место точек в области Д, в которых наклон касательных к решению один и тот же.

Уравнение изоклины:

Естественно, что для некоторых дифф уравнений сущ решение, которое во всех своих точках нарушают условия единственности решения, т.е.в любой окрестности в любой точке этого решения сущ хотябы 2 интегральные прямые, проходящие через эту точку, такие решения будем называть особыми.

В частности особым решением будут огибающие семейства интегральных кривых, если следует отметить то, что особое решение не может получить из общего ни при каком возможном значении параметра С (в том числе С=±∞

Поскольку для особого решения нарушаются условия единственности, то можно предложить след этапы нахождения общего решения.

1)найти множество точек, где частная производная обращаются в ∞.

2)если это множество точек образуют одну или несколько интегральных кривых, проверить являются ли они интегральными дифф уравнениями (1).

3)если это интегральные кривые, то проверить нарушаются ли в каждой точке условия единственности решения, т.е. являются ли эти кривые огибающими.