Содержание

СОДЕРЖАНИЕ 2

ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ 3

1. Построение линейного уравнения парной регрессии 3

2. Расчет линейного коэффициента парной корреляции 6

3. Оценка линейной модели (коэффициент детерминации и F-критерий Фишера) 7

4. Оценка значимости параметров уравнения регрессии с помощью t-статистики 8

5. Точечный прогноз 10

6. Доверительный интервал прогноза 11

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 12

Парная линейная регрессия

По данным таблицы 1 построить линейное уравнение парной регрессии y=ax+b длины кристалла (у) от продолжительности эксперимента (х). Оценить модель и значимость параметров уравнения регрессии. Получить точечный прогноз у для х=112. Построить доверительный интервал прогноза при уровне значимости α=0,05.

Линейная модель парной регрессии имеет вид:

y = ax + b,

где: у – зависимая переменная (результативный признак), х – независимая (объясняющая) переменная, a – коэффициент регрессии, показывающий среднее изменение результата при изменении фактора на одну единицу, если единицы измерения исследуемых показателей одинаковы, b – формальное значение у при х=0.

1. Построение линейного уравнения парной регрессии

Для решения данной задачи средствами Excel имеются следующие возможности:

А. Непосредственный расчет параметров по известным формулам.

Б. Построение уравнения линейной регрессии с помощью тренда. При этом может быть вычислен коэффициент детерминации.

В. Использование процедуры Регрессия надстройки Анализ данных. В этом случае автоматически вычисляется наиболее полный набор характеристик модели. Возможно проведение анализа регрессионных остатков.

Вариант А

Формулы для расчета параметров a и b получены с помощью метода наименьших квадратов:

,

Где: ; ; ; ; .

Промежуточные расчеты для вычисления параметров a и b приведены в табл. 1.

Таблица 1

Вспомогательные расчеты для определения параметров линейной регрессии

№	Продолжительность эксперимента, X	Длина кристалла, Y	XY	X2	Y2	Yx	(Y-Yx)2	(Yx-Yср)2
1	50	19	950	2500	361	21,7	7,5	57,6
2	60	20	1200	3600	400	23,0	8,7	40,7
3	60	21	1260	3600	441	23,0	3,8	40,7
4	70	17	1190	4900	289	24,2	51,3	26,7
5	70	22	1540	4900	484	24,2	4,7	26,7
6	80	25	2000	6400	625	25,4	0,1	15,7
7	80	28	2240	6400	784	25,4	6,9	15,7
8	90	31	2790	8100	961	26,6	19,5	7,6
9	95	25	2375	9025	625	27,2	4,8	4,6
10	100	30	3000	10000	900	27,8	4,9	2,4
11	100	29	2900	10000	841	27,8	1,5	2,4
12	100	33	3300	10000	1089	27,8	27,1	2,4
13	105	35	3675	11025	1225	28,4	43,6	0,9
14	105	32	3360	11025	1024	28,4	13,0	0,9
15	110	30	3300	12100	900	29,0	1,0	0,1
16	110	28	3080	12100	784	29,0	1,0	0,1
17	110	30	3300	12100	900	29,0	1,0	0,1
18	115	31	3565	13225	961	29,6	1,9	0,1
19	115	36	4140	13225	1296	29,6	40,9	0,1
20	115	30	3450	13225	900	29,6	0,2	0,1
21	120	36	4320	14400	1296	30,2	33,5	0,8
22	120	25	3000	14400	625	30,2	27,2	0,8
23	130	32	4160	16900	1024	31,4	0,3	4,4
24	135	34	4590	18225	1156	32,0	3,9	7,3
25	135	25	3375	18225	625	32,0	49,4	7,3
26	140	26	3640	19600	676	32,6	44,0	10,9
27	140	33	4620	19600	1089	32,6	0,1	10,9
28	145	31	4495	21025	961	33,2	5,0	15,3
29	150	36	5400	22500	1296	33,8	4,6	20,3
30	150	33	4950	22500	1089	33,8	0,7	20,3
31	165	32	5280	27225	1024	35,7	13,4	40,0
32	170	35	5950	28900	1225	36,3	1,6	48,0
33	180	38	6840	32400	1444	37,5	0,3	66,3
Сумма:	3720	968	113235	453350	29320	968	427,4	498,0
Среднее	112,7	29,3	3431,4	13737,9	888,5	29,3	13,0	15,1

Дисперсия факторного признака равна:

Дисперсия результативного признака:

Параметры линейной регрессии:

Вариант Б

С помощью Мастера диаграмм построить точечный график зависимости длина кристалла от продолжительности эксперимента. По полученному графику построить линейный тренд (рис. 1).

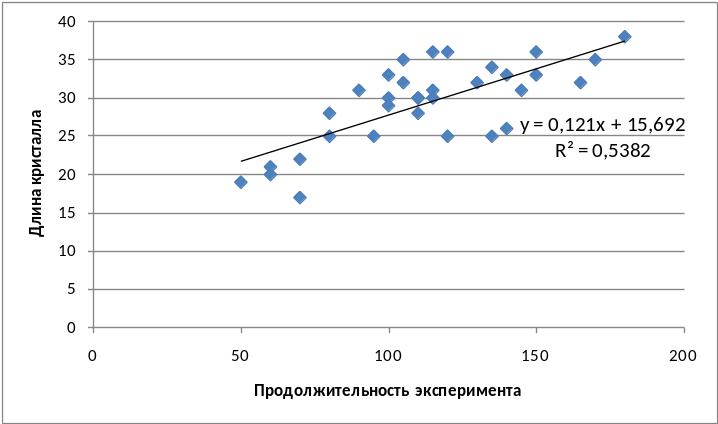
Рис. 1. График зависимости длины кристалла от времени эксперимента

Параметры уравнения соответствуют полученным ранее. Коэффициент детерминации 0,5382 говорит о невысокой точности полученной модели – построенное уравнение регрессии объясняет лишь 53,8% обще вариации результативного признака.

Вариант В

Для построения уравнения линейной регрессии следует обратиться к процедуре Регрессия надстройки Анализ данных (Сервис  Анализ данных  Регрессия).

Результаты процедуры приведены на рис. 2.

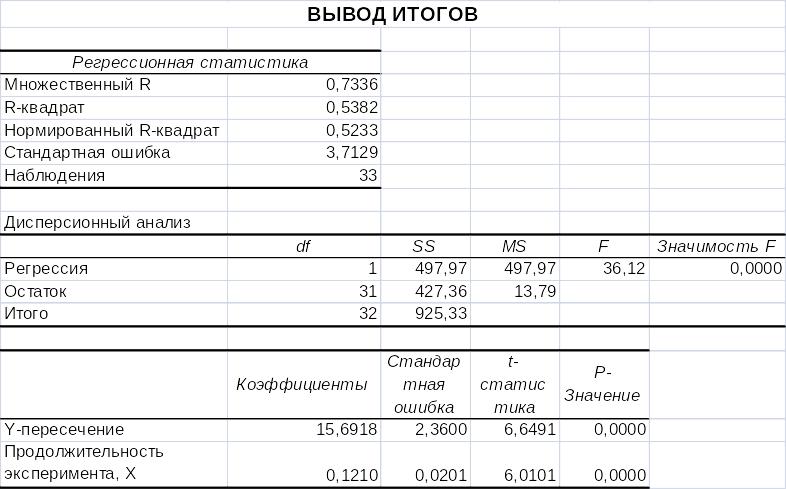
Рис. 2. Результаты процедуры Регрессия

Параметры уравнения регрессии соответствуют полученным ранее. Значение коэффициента регрессии означает, что при увеличении продолжительности эксперимента на одну единицу, длина кристалла увеличится на 0,121 единиц.

Таким образом, зависимость между продолжительностью эксперимента и длиной кристалла имеет вид: