28. Приведение обзих уравнений прямой в пространстве к каноническому виду

Существуют различные виды уравнения прямой на плоскости, описывающие одну и ту же линию. В зависимости от условий задачи удобно использовать тот или иной вид уравнения прямой. Поэтому, полезно уметь переходить от уравнения прямой одного вида к уравнению прямой другого вида. Цель этого пункта статьи заключается в приобретении навыков приведения общего уравнения прямой к другим видам уравнения прямой и обратно.

Начнем с приведения общего уравнения прямой   к каноническому уравнению прямой вида  .

Если  , то переносим слагаемое   в правую часть равенства   с противоположным знаком  . В левой части равенства выносим А за скобки 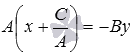 . Полученное равенство можно записать как пропорцию вида  .

Если  , то оставляем в левой части общего уравнения прямой   только слагаемое  , а остальные переносим в правую часть с противоположным знаком:  . Теперь выносим в правой части равенства –B за скобки   и записываем полученное равенство в виде пропорции  . Вот и все.

Запоминать полученные формулы не имеет смысла, проще повторять указанные действия при приведении общего уравнения прямой к каноническому виду.

Пример.

Приведите уравнение прямой   к каноническому виду.

Решение.

Исходное неполное уравнение прямой перепишем как  . Оставляем в левой части равенства только слагаемое  :  . В правой части равенства выносим -3 за скобки:  . Осталось записать полученное равенство в виде пропорции   и на этом приведение общего уравнения прямой к каноническому виду завершено.

Ответ:

29. Нахождение точки пересечения прямой и плоскости

30. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости

31. Поверхности второго порядка

32. Абсолютная величина действительного числа, ее свойства геометрический смысл. Решение неравенств с модулем

33. Определение функций, области определения, области изменения. Способы задания функции, четные и нечетные. Периодичность, монотонность, ограниченные, обратные, явные не явные, параметрически заданные функции

Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Пусть даны два множества Д и Е (Д ( R) (E (R) ) Если каждому числу x € Д по некоторому правилу ( закону f) поставлены в соответствии некоторые элементы y € E, то говорят, что на множестве D определена числовая функция f

Где множество D; D=Д(f) - область определения функции; а множество E; E =E(f) – область изменения функции

Способы задания функции: 1) аналитически (формулой) ;

явно ( прямо дана формула, указывая какие вычислительные операции необходимо совершить над x, чтобы найти y) пример: y= kx + b

или неявно ( Дано уравнение связывающие y и x) y – x = 0

2) графически (графика :D);

3) С помощью соответствия (х – соответствует этому.. и тд)

4) табличный ( таблицей )

Функция может быть четной, нечетной, общего вида

Функция у определенная на на промежутке симметрично относительно оси ОХ и в частности на все числовой прямой называется:

Четной - если любому х из этого промежутка f(-x) = f(x)

Нечетной – если для любого х из этого промежутка выполняется f(-x) = -f(x)

Общего вида: пример f(x) =

Функция равная y=f(x) называется периодической с периодом Т если существует такое Т 0, что для

Функция монотонна т.е. она либо возрастающая, либо убывающая

Функция называется возрастающей(убывающей) на интервале ab, если x1<x2 значит f(x1) < f(x2) или x1<x2 значит f(x1) > f(x2)

Функция называется ограниченной сверху(снизу) на х входящем в Д(f) если существует такое число М

Примеры: y= 1 - (сверху) ; y= (СНИЗУ); y=

Пусть функция задана на множестве Д т.е. f:Д если каждому элементу y соответствует единственный элемент x Д , такой что y=f(x) , то говорят на множестве E определена обртная функция y=f(x)

Явная: функция заданная формулой или данное уравнение разрешено относительно функции

Неявная: - если ее уравнение неразрешимо относительно данной функции

Параметрически заданная: