12. Построение линий влияния кинематическим методом
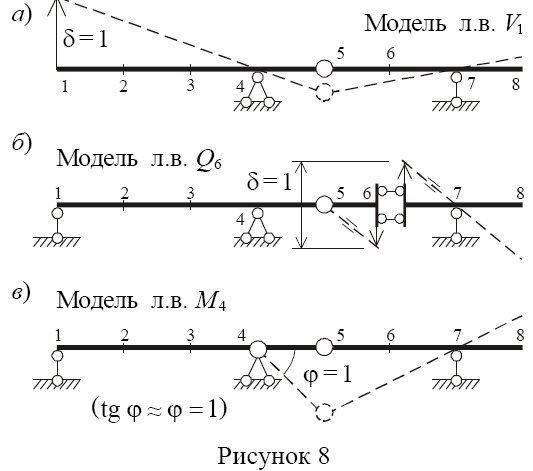
Линия влияния V1. Отбрасываем опорный стержень 1, в результате чего балка превращается в механизм с одной степенью свободы. По направлению реакции отброшенного стержня задаем возможное единичное перемещение δ =1 (рисунок 8, а). При этом диск 1-5 повернется относително опоры 4 и вызовет вращение диска 5-8 относительно опоры 7.
Линия влияния Q6. В сечении 6 врезаем ползун (т. е. отбрасываем связь, соответствующую внутренней поперечной силе). Часть балки справа от шарнира 5 превращается в механизм (рисунок 8, б). Задаем возможное перемещение, соответствующее внутренней поперечной силе – взаимный вертикальный сдвиг δ = 1 дисков, примыкающих к ползуну. Диск 5-6 повернется относительно шарнира 5, диск 6-8 – относительно опоры 7. При этом диски останутся параллельными.
Линия влияния М4. Отбрасывание внутренней связи, соответствующей изгибающему моменту М4, эквивалентно врезанию шарнира в опорное сечение 4 (рисунок 8, в). По направлению внутреннего изгибающего момента во введенном шарнире задаем возможное единичное перемещение φ = 1 (взаимный угол поворота дисков 1-4 и 4-5). На участке 1-4 балка осталась неизменяемой.
13. Определение усилий от различной нагрузки с помощью линий влияния
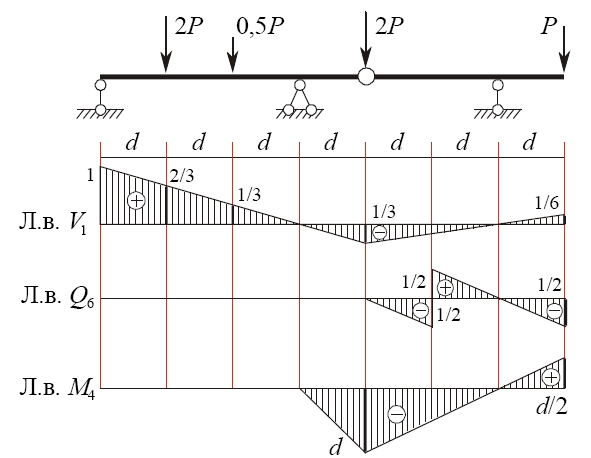
Определим значения V1, Q6 и M4 от заданной нагрузки (рисунок 9). Для этого найдем (с учетом зн ка) ординаты линий влияния под действующими на балку силами (на рисунке 9 выделены жирно). Далее умножим эти ординаты на соответствующие значения сил.
Получим: V1 = 2P · 2/3 + 0,5P · 1/3 + 2P · (–1/3) + P · 1/6 = P;
Q6 = P · (–1/2) = – 0,5 P; M4 = 2P · (–d) + P · d/2 = – 1,5 Pd.
14. Плоские балочные фермы, классификация, расчетная схема, число степеней свободы. Методы расчета.
Расчетная схема плоской фермы представляет собой плоскую шарнирно-стержневую систему, т.е. совокупность прямых стержней, связанных по концам идеальными шарнирами.
примем следующую классификацию ферм:
- по характеру формирования усилий в стержнях фермы:
а) балочные, консольные или консольно—балочные
б) арочные (рис. 4.12, б);
в) висячие (рис. 4.12, в);
г) комбинированные (рис. 4.12
- по очертанию поясов фермы:
а) фермы с параллельным
поясами (рис. 4.12, а);
б) фермы с полигональными поясами (рис. 4.13, а), в частности, треугольные фермы (рис. 4.13,а) и трапецевидные (рис. 4.13, в);
- по конфигурации решетки: рис. 4.13
а)раскосные фермы (рис. 4.12,а);
б) фермы с треугольной решеткой (рис. 4.13) или треугольной решеткой с дополнительными стойками (рис. 4.13, а);
в) полураскосные (рис. 4.14, а), двухраскосные (рис. 4.14, б), и продолжая этот ряд - многораскосные;
г) решетчатые фермы - двухрешетчатые и многорешетчатые (рис. 4.14, в);
д) фермы с составной решеткой (сложные или шпренгельные фермы) (рис. 4.14, г); шпренгелями называют дополнительные малые фермочки, которые можно рассматривать как элементы верхнего или нижнего пояса фермы (рис. 4.14, д).
Расчетная схема
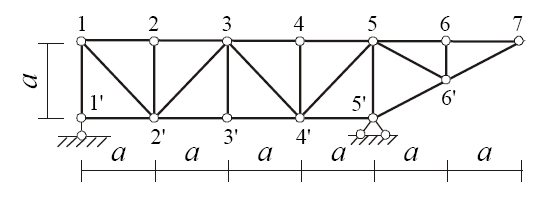
Кинематический анализ фермы
Ферма состоит из 23 стержней (С = 23), соединенных между собой в 13 узлах (У = 13), опирается на землю с помощью трех опорных стержней ( Соп = 3). Определяем число степеней свободы системы по формуле W = 2У – С – Соп = 2 13 – 23 – 3 = 0. Так как W = 0, ферма статически определима и может быть геометрически неизменяемой.
метод вырезания узлов.
Разрезая мысленно стержни, сходящиеся в данном узле, и уравновешивая внешнюю силу, приложенную к нему, продольными усилиями, действующими по направлению каждого стержня, получаем необходимые уравнения для определения этих сил. При составлении уравнений равновесия предполагаем все внутренние силы растягивающими и действующими по направлению от узла.
метод сечений.
Разрезав мысленно ферму на две части и отбросив одну из них, можно составить три уравнения равновесия для оставшейся части фермы. Если в разрез попадают только три стержня, то при помощи этих уравнений можно определить усилия в разрезанных стержнях.
15. Линии влияния усилий в стержнях междуопорной и консольной части фермы. Способы их проверки.
Следует различать два вида сечений: междуопорное и консольное. Междуопорное сечение разделяет ферму на две части, в каждой из которых находится одна из опор. Консольное сечение так же делит ферму на две части, причем одна из них свободна от опорных реакций. Способ построения линии влияния зависит от вида сечения.
Междуопорное сечение:
1) строят линии влияния опорных реакций;
2) проводят сечение не более чем через три стержня, в том числе и ра ссматриваемый;
3) составляют уравнения Y = 0 или М = 0 правой части фермы, когда груз
Р = 1 слева от сечения, и левой части, когда груз справа от сечения. При этом в уравнение должны входить только искомая продольная сила и одна из опо рных реакций;
4) передаточная (соединительная) прямая находится между узлами рассеченного стержня грузового пояса, левая прямая – слева от передаточной,правая – справа;
5) если используется уравнение моментов, то левая и правая прямые пересекаются под моментной точкой.
Консольное сечение:
1) проводят сечение не более чем через три стержня, в том числе и ра ссматриваемый;
2) составляют уравнения Y = 0 или М = 0, когда груз Р = 1 слева и справа от сечения, всегда рассматривая равновесие отсеченной консоли. При этом в уравнение должны входить только искомая продольная сила и груз Р = 1;
3) если используется уравнение моментов, то координату z груза отсчитывают от моментной точки;
4) передаточная (соединительная) прямая находится между узлами рассеченного стержня грузового пояса, левая прямая – слева от передаточной, правая – справа.
16. Шпренгельные фермы. Линии влияния в их стержнях
Шпренгель – это дополнительная двухопорная фермочка, вводимая в с остав каждой панели для восприятия местной нагрузки и передающая давление на узлы основной фермы.
Преобразуем нашу ферму в шпренгельную, установив одноярусные шпре нгели в верхнем грузовом поясе (рисунок 6). Для примера рассмотрим только ее междуопорную часть.
Определяются эти усилия из тех же уравнений, что и ранее, только меняются границы передаточных прямых.
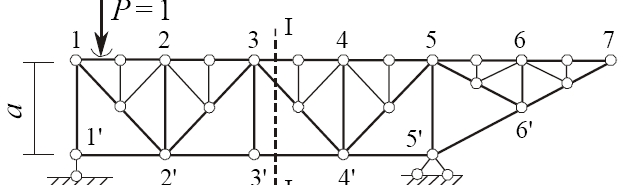
+ 15 билет ( способы построения).