9. Неоклассическая теория спроса на инвестиции

Согласно концепции неоклассиков, предприниматели осуществляют инвестирование с целью достижения оптимального размера капитала. Поэтому функцию инвестиционного спроса можно представить:

I^a = β(K* – K_t); 0 < β < 1,

где: I^a – объем автономных инвестиций на период t;

K_t – фактический объем капитала;

К* – оптимальный объем капитала;

р – коэффициент, характеризующий меру приближения существующего капитала к оптимальному за период t.

Определение оптимального объема капитала

1. Оптимальный объем капитала обеспечивает при существующей технологии максимальную прибыль.

2. В условиях совершенной конкуренции прибыль максимальна, когда предельная производительность капитала (r) равна предельным издержкам, которые состоят из нормы амортизации (d) и ставки процента по финансовым активам (i), которые представляют альтернативные затраты использования средств в качестве капитала.

Прибыль максимальна, если r=d+i.

Для определения оптимального размера капитала используем производственную функцию Кобба-Дугласа:

Y= K^ax L^l-^a; 0< а <1,

где: а – параметр, по которому определяется вклад капитала в выпуск продукции.

Используя условие максимизации прибыли, оптимальное значение капитала будет равно:

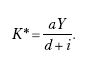
Если при заданном значении предельных издержек изменится технология производства, то значение К* тоже изменится. Если из-за научно-технического прогресса растет предельная производительность капитала, то К* также увеличится (при неизменной ставке процента).

Таким образом, инвестиционный спрос есть возрастающая функция от предельной производительности капитала и убывающая функция от ставки процента (при заданном значении амортизации).

Неоклассическая функция инвестиций более объективна по сравнению с кейнсианской, так как она определяется технологией производства в отличие от кейнсианской, которая зависит от R*, соотношения оптимизма и пессимизма инвесторов. Кейнсианская функция инвестиций имеет меньшую эластичность по ставке процента, чем неоклассическая.

10. Модели инвестиционного процесса

Для анализа реальной динамики инвестиций (или инвестиционного процесса) предложено несколько эконометрических моделей.

Модель акселератора инвестиционного процесса.

В основе модели лежит постулированное предположение - существует устойчивая зависимость между величиной капитала, необходимого фирме, и объемом выпуска.

Начальные и граничные условия модели:

- отношение желаемой величины капитала к объему выпуска (h) принято постоянным;

- инвестиции всегда достаточны для поддержания величины основного капитала на желаемом уровне от периода к периоду.

Предполагается, что желаемый размер капитала (K*) представляет собой постоянную долю (h) выпуска (Q):

K* = hQ

Если фирма в состоянии инвестировать немедленно, чтобы фактическая величина основного капитала была равна его желательному уровню, то K* всегда будет равным К. Тогда чистые инвестиции (J) должны составить:

J= K*+1 - K = hY+1 - hY = h(Y+1 -Y),

где J - чистые инвестиции, равные приросту основного капитала.

Это очень простое соотношение содержит весьма важную информацию: размер чистых инвестиций пропорционален изменению выпуска, а не его уровню.

Теперь понятно, в чем заключается так называемая теория акселератора инвестиционного процесса: инвестиции растут, когда ускоряются темпы роста производства.

Исходя из постоянной нормы амортизации основного капитала (d), то амортизация капитала равна dK и выражение для валовых инвестиций можно записать в виде:

I = h(Y+1 - Y) + dK,

Модель имеет два слабых места:

Величина капитала (h) не может быть постоянным, т.к. стоимость капитала является функцией рыночных ставок процента и законов о налогообложении инвестиций.

Инвестиции не достаточны для поддержания величины основного капитала на желаемом уровне, т.к. издержки, связанные с выбором величины основного капитала, неизбежных лагов при его освоении и объем производства в следующем периоде обычно точно не известен.

Подход на основе издержек регулирования.

Простейшим усовершенствованием данной модели явилось введение механизма частичного регулирования, описывающего постепенное приближение К к желаемому уровню К*:

J = K+1 - K = g(K+1 - K),

где g - коэффициент частичного регулирования и имеющий диапазон значений 0 < g < 1.

Когда g = 1, мы получаем модель акселератора инвестиционного процесса, поскольку K+1 = K*+1.

Когда g < 1, фактическая величина K регулируется лишь постепенно. Таким образом, g определяет скорость приближения фактического объема основного капитала к оптимальному желаемому объему.

Определим, что именно определяет скорость приближения К к К*.

Предположим, фирма получает прибыль меньше ожидаемой всякий раз, когда K+1 не равен K*+1. Фирма несет потери в размере c1(K*+1 - K)2, где c1 является константой. Ясно, что потери отсутствуют, когда K+1 = K*+1, и они становятся больше с увеличением разницы. Мы предполагаем, что в действительности потери пропорциональны квадрату разницы между K и K* (квадратичная функция потерь). Например, если разница между К и K* удваивается, то потери фирмы увеличиваются в 4 раза.

Предположим также, что фирмы несут издержки всякий раз, когда уровень чистых инвестиций высок. Допустим, что инвестиционные издержки тоже квадратичные, так что инвестиционные издержки равны c2(K+1 - K)2, где c2 - константа. Вспомним также, что K+1 - K равно уровню чистых инвестиций. Общие потери определяются по формуле:

Потери = c1(K*+1 - K)2 + c2(K+1 - K)2.

Поскольку фирма пытается минимизировать потери потенциальной прибыли, вытекающие из принятого ею инвестиционного решения, ей приходится уравновешивать квадратичные издержки двух видов: связанные с отклонением размера основного капитала от желаемого уровня и с чрезмерно быстрым ростом инвестиционных расходов. Фирма максимизирует свои прибыли путем выбора такого уровня К который сводит к минимуму потери в данном соотношении.

Легко показать (хотя для этого необходимы соответствующие расчеты), что оптимальная величина K+1 определяется из соотношения

Когда очень велико значение c2 а также высоки издержки, связанные с ускоренным ростом инвестиций, g приближается к нулю. В этом случае приближение величины основного капитала к желаемой происходит весьма постепенно.

Когда фирме неизвестна производительность при данной технологии производства, т.е. она не знает, каков будет объем выпуска при данной величине капитала, целесообразно постепенное изменение основного капитала, если фирма стремится максимизировать ожидаемые прибыли даже при не квадратичных издержках регулирования инвестиций.

q-теория Тобина.

Джеймс Тобин из Йельского университета, в 1982 г. получивший Нобелевскую премию по экономике, предложил еще одну модель динамики инвестиций, основанную на идее издержек регулирования. Известная q-теория инвестиций Тобина исходит из того, что стоимость фирмы на фондовом рынке помогает измерить разрыв между K и K*+1.

Переменная q определяется как отношение стоимости фирмы на фондовом рынке к восстановительной стоимости ее основного капитала.

Понятие "восстановительной стоимости капитала" представляет собой издержки замещения капитала, на которые пришлось бы пойти при приобретении предприятия и оборудования фирмы на рынке продукции.

Если фирма стоит 150 млн. долл. на фондовом рынке, а ее восстановительная стоимость составляет 100 млн. долл., то q будет равно 1,5. Таким образом, q характеризует стоимость приобретения фирмы на финансовом рынке в сравнении со стоимостью покупки ее капитала на рынке продукции [3, c.160].

Если:

q > 1, тогда K*+1>К, поэтому инвестиции должны быть значительными.

q < 1, тогда K*+1<К, поэтому инвестиции должны быть небольшими.

Очевидно, что стоимость фирмы на фондовом рынке V равна дисконтированной стоимости дивидендов, выплаченных фирмой. Значит, дисконтированная стоимость дивидендов на единицу капитала составляет V/K. Если восстановительная стоимость капитала фирмы равна К, тогда V/K, по определению, будет q-стоимостью фирмы.

Текущий уровень инвестиций может зависеть скорее от текущего, чем от постоянного, дохода, если фирма ограничена в денежных средствах.

То же самое относится к фирме, сталкивающейся с рационированием кредитов, - величина инвестиционных расходов может зависеть скорее от текущего потока наличности, чем от дисконтированной предельной производительности капитала.

Рационирование кредитов обусловлено двумя важнейшими причинами:

неравновесными процентными ставками, когда государственные органы устанавливают для кредитных учреждений предельные уровни ставки ссудного процента, в целях макроэкономического регулирования;

различиями оценки рисков в условиях неопределенности.

Таким образом, рационирование кредитов наряду с издержками регулирования оказывается еще одной причиной постепенности приближения величины основного капитала к желаемому уровню.

Таким образом, основными моделями инвестиционного процесса являются модель акселератора инвестиционного процесса, модель издержек регулирования и модели, основанные на рационировании кредитов. Однако, ни одна из этих моделей не может быть признана превосходящей остальные.