1. Введение

В курсе геометрии 10-11 классов большое внимание уделяется декартовым координатам, векторам и их применению при решении задач. Уравнения простейших геометрических объектов – прямой и плоскости, дают более наглядную картину численного восприятия пространства. Учащимся, занимающимся в классах с углублённым изучением информатики, в физико-математических классах, изучение данной темы даёт возможность непосредственно использовать свои знания по данной теме при разработке и применении программ трёхмерной графики. С некоторыми оговорками некоторые из следующих материалов можно использовать и в 8-9 классах в при изучении темы «Уравнение прямой на плоскости».

2. Уравнение прямой

Для вывода уравнения прямой в пространстве удобней всего воспользоваться условием коллинеарности векторов. Рассмотрим прямую в пространстве, при этом пусть точка - известная точка, лежащая на этой прямой, и пусть вектор - известный вектор, коллинеарный прямой Данный вектор называется направляющим вектором прямой. Рассмотрим точку - произвольную точку пространства. Для того, чтобы выполнялось условие необходимо и достаточно, чтобы Найдём У коллинеарных векторов координаты пропорциональны, значит, Полученное уравнение является каноническим уравнением прямой

Преобразуем полученное уравнение следующим образом. Пусть

Тогда где Полученная система называется параметрическим уравнением прямой Задавая различные значения параметра получим различные точки на прямой Так, например, при получим точку Таким образом, параметр выполняет роль внутренней координаты на прямой.

Задача 1

Написать уравнение прямой, проходящей через точки

Решение

Направляющим вектором прямой будет Отсюда уравнение прямой имеет вид Уравнение в параметрическом виде имеет вид

Задача 2

Написать уравнение прямой, содержащей медиану треугольника если

Решение

середина значит, Таким образом, Направляющим вектором искомой прямой будет вектор Отсюда уравнение прямой имеет вид а в параметрическом виде

Задача 3

Написать уравнение прямой, содержащей высоту треугольника если

Решение

Высота Пусть

уравнение прямой имеет вид причём координаты точки удовлетворяют этому уравнению.

С другой стороны, значит, их скалярное произведение равно Так как то

Отсюда, координаты точки удовлетворяют системе

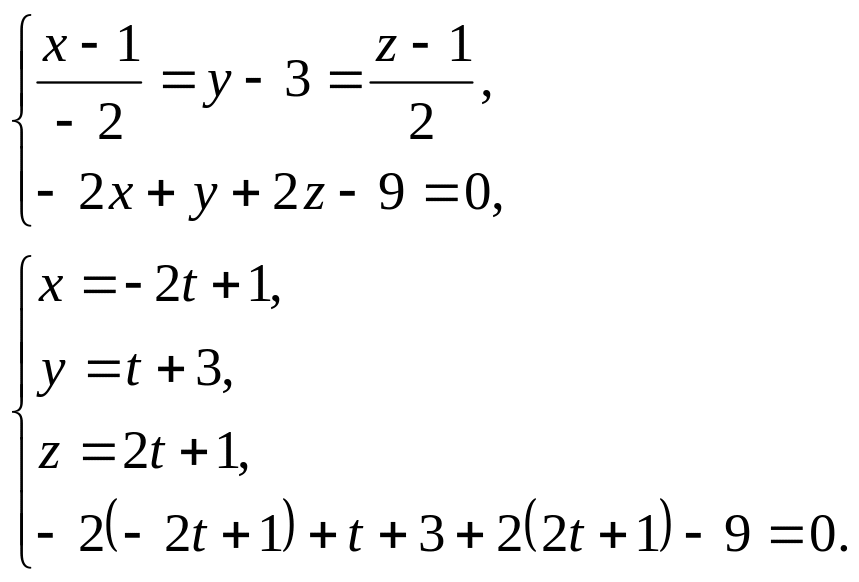
Решив последнее уравнение, найдём Отсюда, точка Значит, вектор и, следовательно, уравнение прямой имеет вид

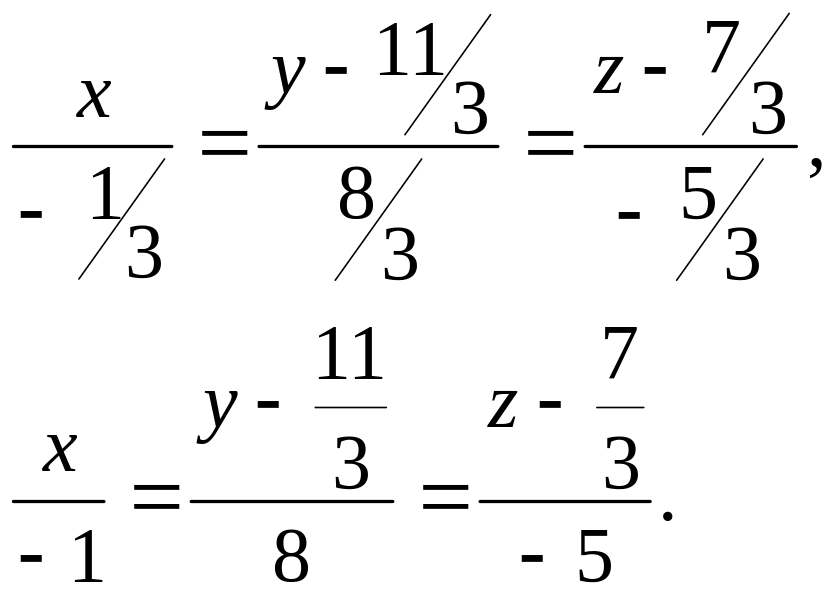
3. Уравнение плоскости

Для вывода уравнения плоскости воспользуемся условием перпендикулярности векторов. Рассмотрим плоскость Пусть точка известная точка, принадлежащая данной плоскости, и пусть вектор известный вектор, перпендикулярный плоскости Такой вектор называется нормальным вектором (нормалью) плоскости. Точка произвольная точка пространства. Для того, чтобы выполнялось условие необходимо и достаточно, чтобы вектора и были перпендикулярны, следовательно, скалярное произведение этих векторов должно быть равно

Обозначим Отсюда Полученное уравнение является уравнением плоскости

Задача 4

Написать уравнение плоскости, проходящей через середину отрезка перпендикулярно к нему, если

Решение

Найдём координаты точки середины отрезка

нормальный вектор искомой плоскости.

Отсюда искомое уравнение имеет вид

Итак, искомое уравнение.

Задача 5

Написать уравнение плоскости, проходящей через начало координат, перпендикулярно прямой

Решение

Направляющий вектор данной прямой будет нормалью к искомой плоскости, следовательно, Тогда уравнение плоскости имеет вид

Задача 6

Написать уравнение плоскости, проходящей через точки

Решение

Так как координаты найденных векторов не являются пропорциональными, то и неколллинеарны, а значит, точки не лежат на одной прямой. Через три точки, не лежащие на одной прямой можно провести единственную плоскость. Нормальный вектор этой плоскости должен быть перпендикулярен любому вектору, лежащему в плоскости, а по критерию перпендикулярности прямой и плоскости для этого необходимо и достаточно перпендикулярности каким-либо двум неколлинеарным векторам, лежащим в плоскости. Пусть нормаль Тогда

Найдём координаты нормали из системы

Пусть Тогда

Таким образом а уравнение искомой плоскости имеет вид