35.Роль аналитич группировки в изучнии взаимосвязи явлений

36.Коэф детерминации и его значение

37.Изучение взаимосвязи графич методом

38.Ранговый коэф корреляции, коэф коррел Фехнера. При наличии количеств признаков исп-ся коэф Фехнера и коэф Спирмена. Коэф Фехнера - мера тесноты связи - отношение разности числа пар совпадающих и несовпадающих пар знаков к сумме этих чисел: , где С – кол-во совпад знаков отклонений X и У от их средней; Н – кол-во несовпад знаков отклонений от средней. (С+Н=n) Коэф Фехнера не учитывает величину отклонений признаков от ср значений, но он м служить некоторым ориентиром в оценке интенсивности связи. В данном случае он указывает на тесную связь признаков. Ранговый коэф Спирмэна где разность рангов по обоим признакам для каждого объекта, i = 1,...,n.

39.Построение паралл рядов и количеств оценка их взаимосвязи

40.Пок-ль тесноты связи качеств признаков. При наличии качеств (атрибутивных) признаков рассч-ся: коэф ассоциации, коэф контингенции, коэф сопряж-ти К.Пирсона, коэф сопряж-ти А.Чупрова. Коэф ассоциации , где a,b,c,d- частоты четырехклеточной таблицы. Наличие связи определяется от 0,3. Коэф контингенции

Наличие связи опред-ся от 0,5. Коэф сопряж-ти К.Пирсона , где φ - сумма квадратов частот каждой строки группы признака, деленных на сумму частот по колонкам и, в свою очередь, на сумму частот по строке без единицы; , где Коэф сопряж-ти А.Чупрова

, где число групп по колонкам, число групп по строкам.

41.Динамич ряды, осн эл-ты и правила их построения. Одной из важнейших задач статистики яв-ся изучение изменений анализируемых пок-лей во времени, т.е. их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов). Ряд динамики – это числовые значения опред стат пок-ля в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке). Числовые значения того или иного стат пок-ля, составляющего ряд динамики, называют уровнями ряда и обычно обозначают через y. Первый член ряда y1 называют начальным (базисным) уровнем, а последний yn – конечным. Моменты или периоды времени, к к-ым относятся уровни, обозначают через t. Ряды динамики, как правило, представляют в виде таблицы или графически, причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.

42.Абс и относ пок-ли динамики. Абс: абс прирост, абс ускорение, абс значение 1% прироста. Абс прирост (снижение) ряда это абс разность между текущим уровнем и предшествующим ему. Абс ускорение (замедление) - разности между скоростями. Абс прирост хар-ет увеличение либо уменьшение уровня ряда за опред период времени. Если производится сравнение с пред периодом, то абс приросты яв-ся цепными Если за базу сравнения принимается какой-то опред ур, то такие абс уровни будут базисными Ускорением наз-ся разность между послед и пред абс приростом. Ускорение показывает насколько данная скорость больше (меньше) предыдущей. Если уровни ряда выражены в относ величинах, то абс прирост и ускорение выражаются в пунктах (а не в процентах). Абс значение 1% прироста Представляет собой одну сотую часть пред уровня. Его можно определить как отношение абс прироста к соответствующему темпу прироста

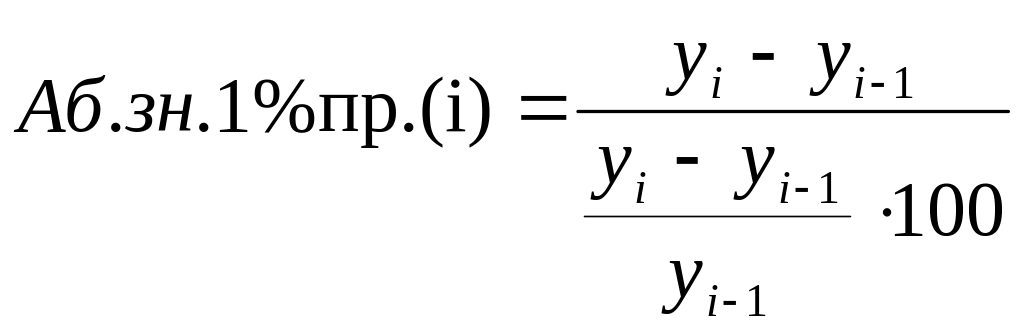Относ: коэф роста, коэф прироста, темп роста, темп прироста. Коэф роста - это отношения выбранного уровня динамического ряда к предшеств ему или к базисному. В зав-ти от этого различают ценные и базисные коэф-ты роста. Выбор баз уровня предполагает подробное знание изучаемого явления, его сути и требует глубоких познаний в данной области. Сравнение с нетипической базой приводит к неверно определяемой тенденции развития. Коэф роста, умнож на 100%, наз темпами роста. Темп изменения (роста, снижения) - это отношение отчетного уровня к сравниваемому - пред или баз, представленное в %. Цепной Баз Темп прироста характеризует относ скорость изменения уровня ряда в единицу времени. Рассч-ся как отношение абс прироста к ур ряда, взятому за базу сравнения (в %). П=Т-100% или Различают темп прироста: цепной и базисный.

43.Ср величины в динамич рядах. Ср хронологические (интерв ряда, моментного ряда), ср абс прирост, ср темп роста, ср темп прироста. Ср пок-ли динамики - ср ур ряда, ср абс изменения и ускорения, ср темпы роста – хар-ют тенденцию. Они необходимы при обобщении характеристик тенденции за длит период, по разл периодам и незаменимы при сравнении развития за неодинак по длит-ти отрезки времени, при выборе аналитич выражения тренда. Ср ур интерв динамич ряда. Для разных видов рядов динамики ср ур рассч-ся неодинаково. В интерв ряду абс величин с равными периодами (интервалами):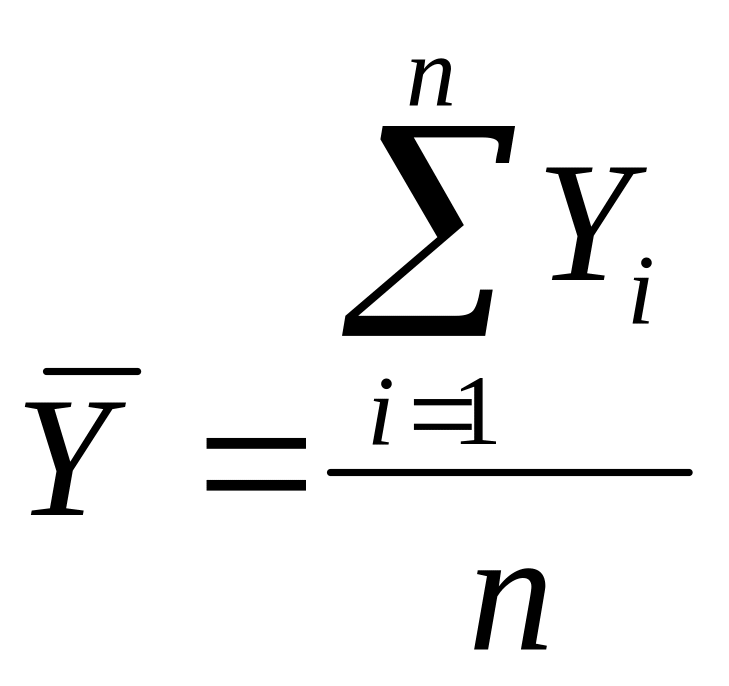 Для моментного ряда с равными промежутками между датами (моментами): Для мом ряда с неравными промежутками между датами (моментами): 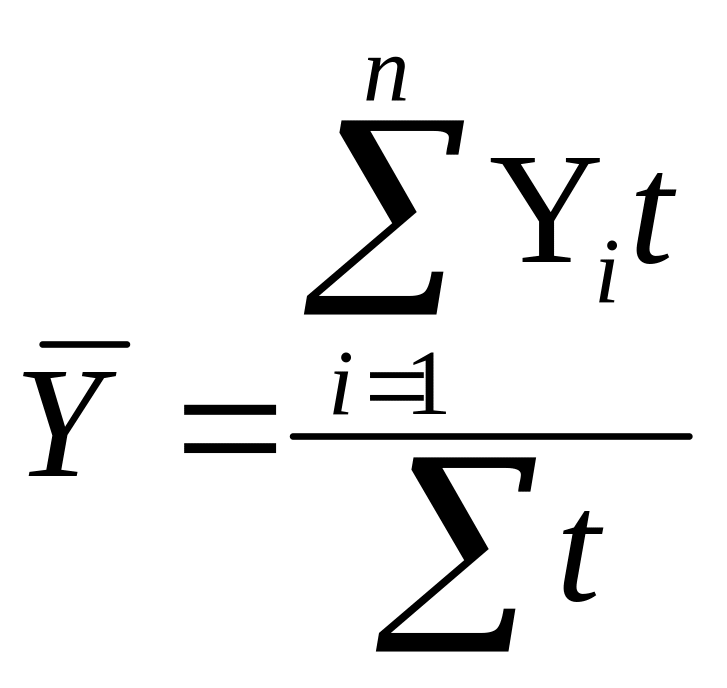где t - время. Напр, с 1 числа месяца по 18 в блоге было оставлено 45 коммент, с 19 по 27 – 48, а с 28 по 31 - 54, то ср число комментариев за месяц составит: комментария.

Ср абс прирост 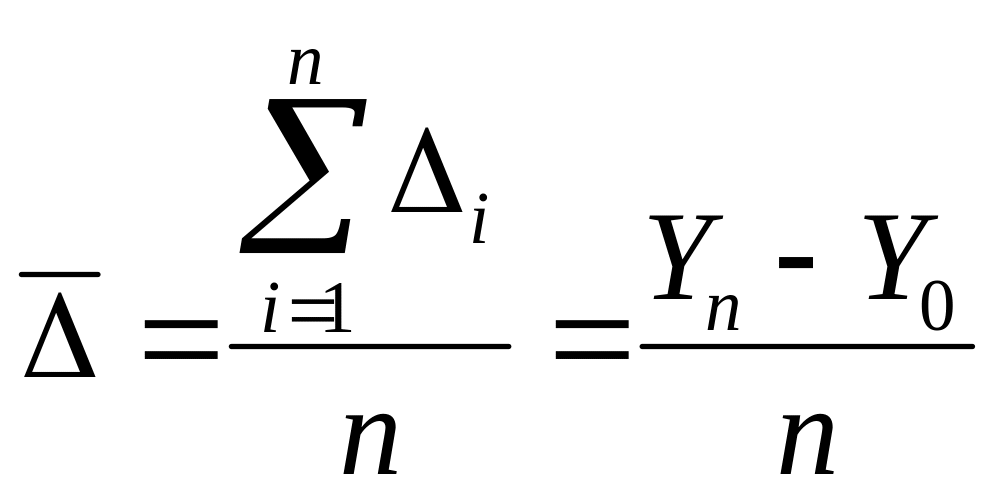При наличии существенной колеблемости уровней ср абс прирост, как и ср темп, определяется по тренду. Ср темп изменения 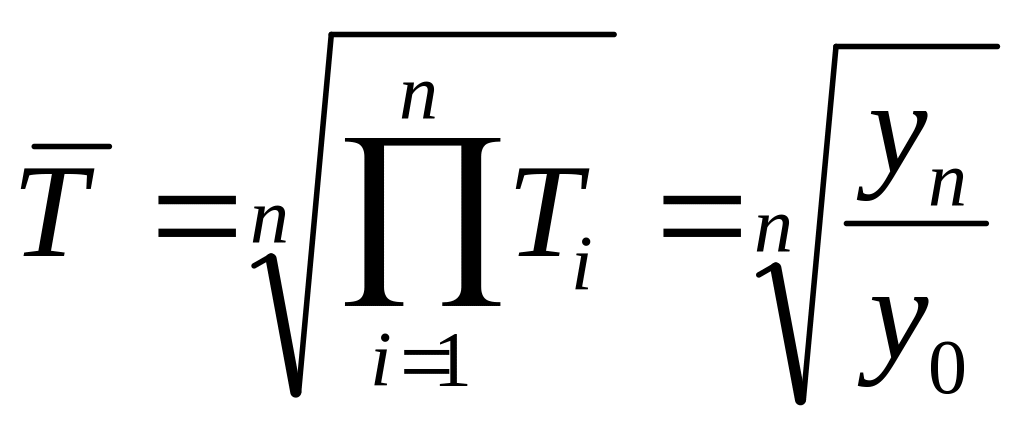и ср темп прироста

Ср пок-ли динамики как параметры трендов: ср абс прирост - параметр линейного тренда; ср ускорение - параметр параболического тренда; ср темп роста - параметр экспоненциального тренда.

44.Методология выявления тренда в динамич рядах. Осн тенденция динамики. Нахождение осн тенденции изменения ур динамич ряда предполагает ее количеств выражение, в опред степени свободное от воздействия случайных факторов. Выявление осн тенденции развития (тренда) наз-ся в статистике выравниванием. Методы выявления осн тенденции динам ряда априори:

1) По существу изучаемых явлений (теорет анализ)

2) Построение графического изображения

3) Механич метод: метод укрупнения интервалов (первоначальный ряд заменяется др, уровни к-го хар-ся значительно большими по продолжительности времени значениями); усреднение полученных укрупненных уровней за ряд лет; сглаживание по скользящей средней (объединение отд периодов в группы и исчисления средних, но со сдвигом на 1, 2 или более периодов; интервал сглаживания желательно выбирать по нечетному числу уровней, то есть 3,5,7...)

4) Проверка гипотезы о различии ср показателей динамики: дисперс анализ (если ряд разбит на 3-5 периодов); в разл частях динам ряда (если ряд разбит на 2 части).

Аналитическое выравнивание - метод измерения параметров тренда. Прослеживая (обычно на графике) развитие отд соц-эк явления за ряд лет, можно подобрать теорет кривую (аналитическую ф-ию), достаточно хорошо аппроксимирующую эмпирический ряд: прямую; параболу; экспоненту; логарифмическую кривую и др. Рассм аналит выравнивание ряда динамики по прямой: . t - порядковый номер периода или момента времени. Методом наим квадратов рассч-ся параметры а и b на основе системы нормальных ур-ий:

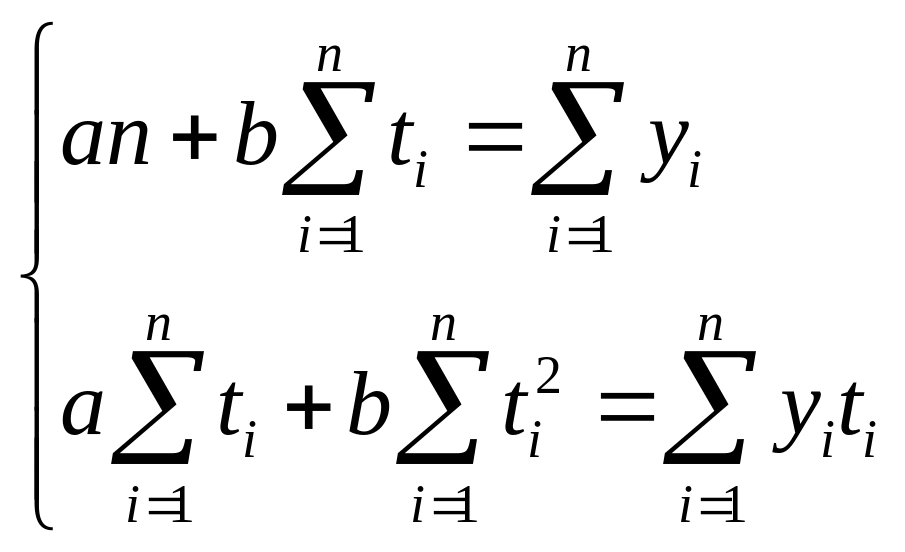
Нахождение параметров а и b упрощенным способом, при к-м переносят начало координат в середину динам ряда:

,

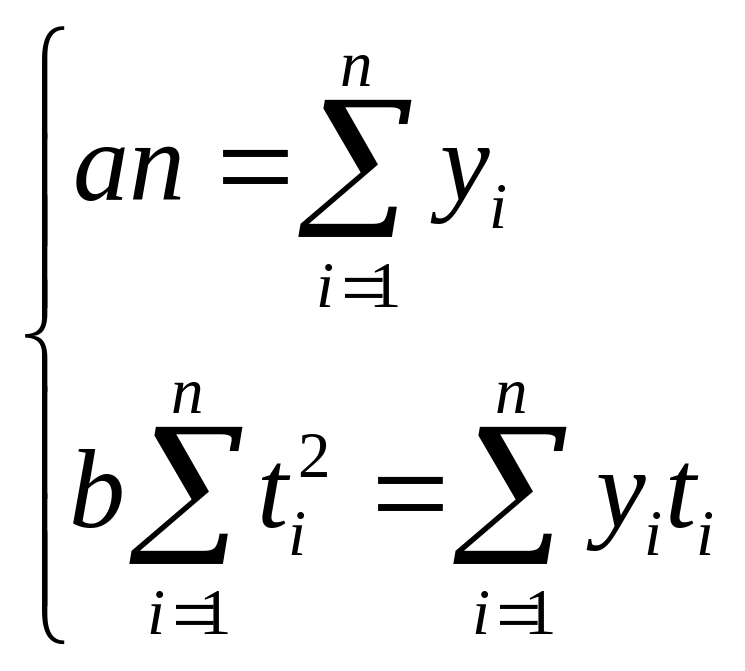
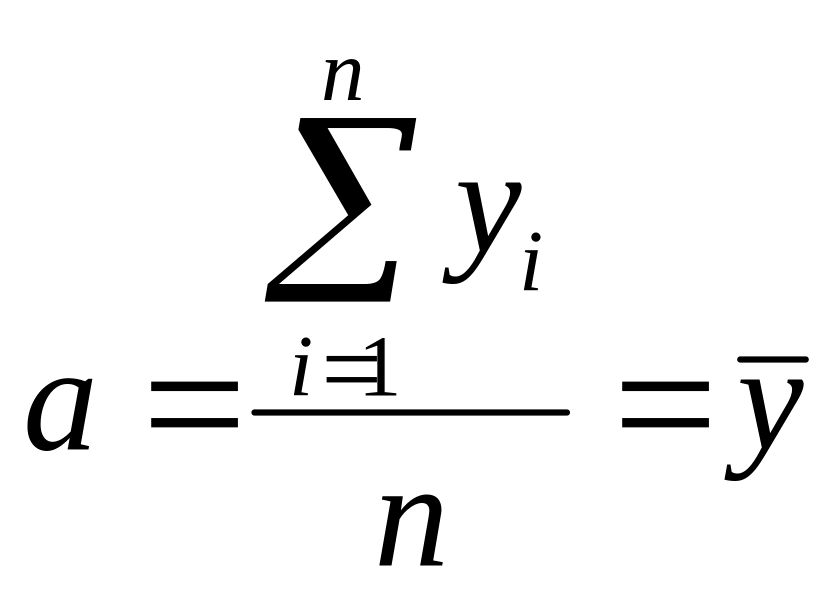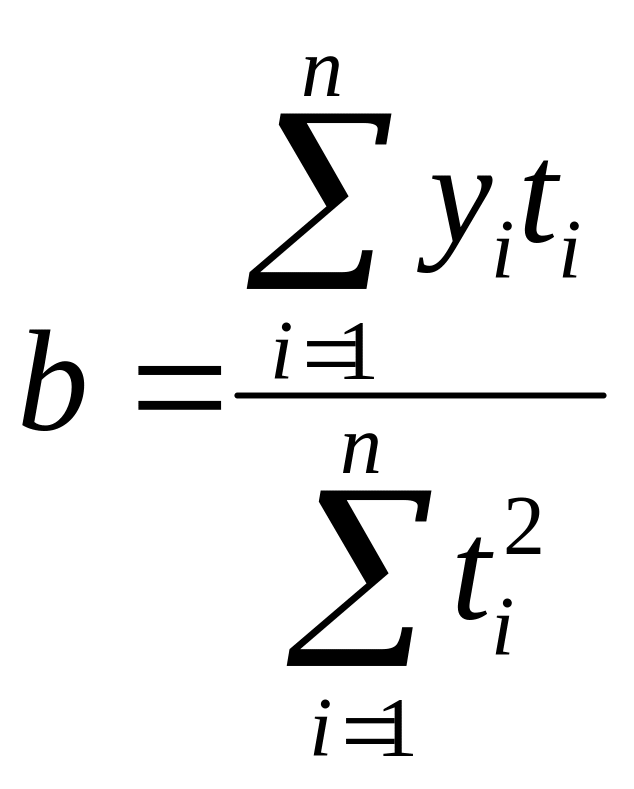
Апостериорная проверка правильности выбранного типа тренда: 1) Проверка значимости найденных параметров уравнения. 2) Проверка на основе суммы квадратов отклонений фактических значений от теорет (рассчитанных по тренду). Из сов-ти кривых выбирается та, к-ой соответствует миним значение критерия (данная проверка производится по ур-ям, имеющим одинаковое число параметров).

45.Интерполяция и экстраполяция уровней динам ряда. Важным моментом при анализе динам рядов яв-ся их интерполяция - нахождение недостающих уровней внутри ряда, а также экстраполяция - нахождение уровней за пределами рассм периода. Экстраполяция бывает перспективной и ретроспективной. Экстраполяция, как метод статистики, является одним из способов прогнозирования и научного предвидения. Существенной проблемой в данной теме является изучения взаимосвязей в динамике.

46.Понятие о сезонных колебаниях. Индексы сезонности, их расчет и графич изображение.

47.Индексный метод в экономико-статистич анализе

48.Индексы индивид и сводные

49.Средние индексы

50.Баз и цепные индексы. Пост и переем веса индексов

51.Понятие стат графиков и требования, предъявляемые к ним

52.Виды стат графиков, особенности применения и анализа

53.Корреляц поле, правила построения и особ-ти анализа

54.Изучение формы распределения

55.Норм распред и его хар-ки В 1727 Абрахам де Муавр открыл закон распределения вероятностей, названный законом норм распределения. Разработкой вопросов, относящихся к данному закону, занимались Пьер Лаплас и Карл Гаусс. Общие условия возникновения закона норм распред установил Ляпунов. Норм распред образ-ся, если на варьирующую переменную влияет большое число факторов, ни один из которых не имеет преобладающего влияния. Закон норм распред лежит в основе многих теорем и методов статистики при оценке репрез-ти выборки (расчете ошибки выборки и распространении хар-тик выборки на ген сов-ть); измерении степени тесноты связи и составлении модели регрессии; построении и использовании стат критериев.. Распределение непрерывной случайной величины х называют норм N (х, ), если соответствующая ей плотность распределения выражается ф-лой:

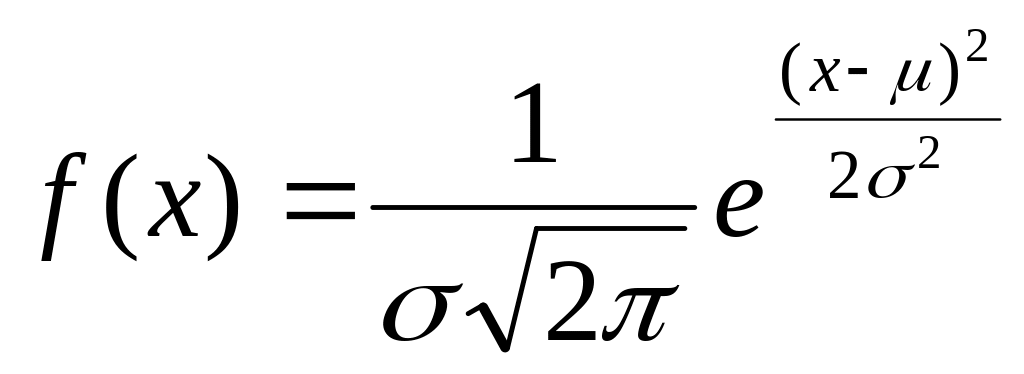
Свойства норм распред:

• Значения признака имеют тенденцию концентрироваться около точки t = 0, где 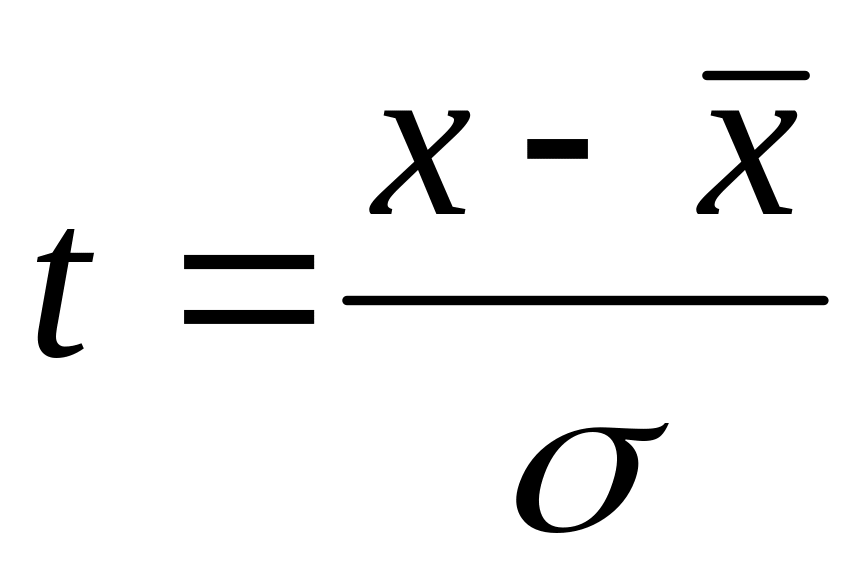яв-ся нормиров откл-ем.

• Норм кривая симметрична относительно вертик оси.

• Значения наблюдений не ограничены по своей величине.

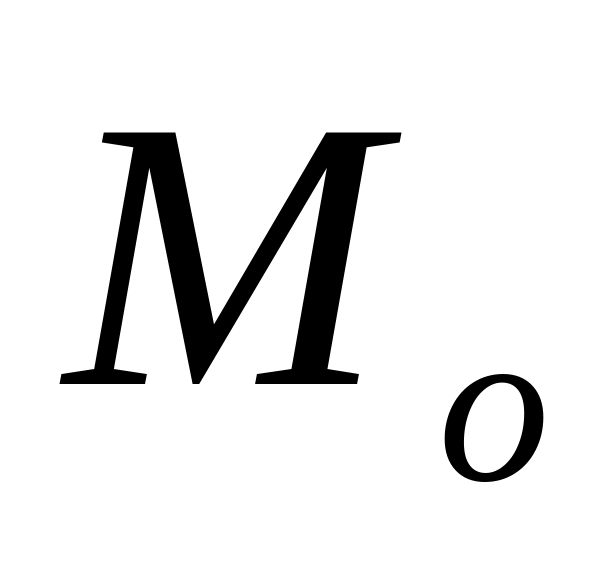• , и 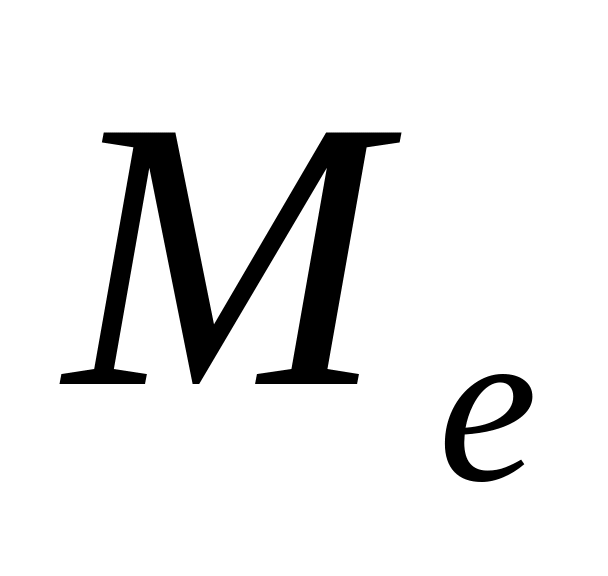имеют одно и то же значение при t = 0.

• Изменения величины t характеризует разл типы распред.

С колебаниями ср величины, кривая норм распределения будет смещаться по оси абсцисс влево или вправо, тогда как форма кривой останется неизменной.

56.Критерии согласия: Пирсона, Романовского, Ястремского. Для проверки гипотезы о соответствии эмпирич распределения теоретич закону норм распределения исп-ся особые стат показатели - критерии согласия (или критерии соответствия). К ним относятся критерии Пирсона, Колмогорова, Романовского, Ястремского. Критерий согласия Пирсона где m – частота эмп распределения, m' - частота теорет распред. Табличное значение хи-квадрат опр-ся при пом числа k - числа степеней свободы, равного разности между числом групп (r) и величиной 3 для выравнивания по закону норм распр-я, т.е. k = r-3. Если , то расхождения между теорет и факт распр-ем считается неслучайным. Если , то расхождения между теорет и факт распределением считается случайным, а распределение хорошо согласуется с з-м норм распр-ия. Критерий согласия Романовского где k - число степеней свободы. Если R<3, расхождения между теорет и эмп частотами считаются случайными. Если R>3, то неслучайными, существенными. Критерии согласия Пирсона и романовского не показывают, чем конкретно отл-ся рассматриваемые распределения. С этой целью применяются спец пок-ли асимметрии и эксцесса. Критерий согласия Ястремского где r - число групп. Величина имеет табличное значение, равное 0,6 для распределений, где число групп представлено до 20. Если , расхождение между теорет и эмп распределениями считаются случайными. Если , расхождение между теорет и эмп распределениями неслучайны, т.е. эмп распределение не отвечает требованиям норм распределения. Критерий согласия Колмогорова Вероятность Р( ) может изменяться от 0 до 1. Если принимает значения до 0,3, то Р( )=1, след-но отклонений между эмп и теорет частотами нет.

57.Критерий согласия Пирсона где m – частота эмп распределения, m' - частота теорет распред. Табличное значение хи-квадрат опр-ся при пом числа k - числа степеней свободы, равного разности между числом групп (r) и величиной 3 для выравнивания по закону норм распр-я, т.е. k = r - 3. Если , то расхождения между теорет и факт распр-ем считается неслучайным. Если , то расхождения между теорет и факт распределением считается случайным, а распределение хорошо согласуется с законом норм распр-ия.

58.Коэф-ты ассиметрии и эксцесса. Коэф асимм К_А хар-ет асимметричность распределения признака в сов-ти. Пок-ль эксцесса E_X представляет собой отклонение вершины эмп распред вверх или вниз («крутость») от вершины кривой норм распред. Асимм распределения: при K_A=0 распред считается норм; при К_А>0 правосторонняя асимм; при К_А<0 левосторонняя асимм; если асимм более 0,5, то независимо от знака она считается значительной; если асимм меньше 0,25, то она считается незначительной.

Расчет асимметрии распределения при помощи нормированного момента 3 порядка дает наиболее точный результат , т.е. нормированный момент третьего порядка. Для оценки существенности асимметрии вычисляют пок-ль ср квадратич ошибки коэф асимметрии. Если отношение имеет значение больше 2, то это свидетельствует о существенном хар-ре асимм. Эксцесс распределения. Пок-ль эксцесса Е_Х представляет собой отклонение вершины эмп распред вверх или вниз («крутость») от вершины кривой норм распред, НО! график распределения может выглядеть сколь угодно крутым в зав-ти от силы вариации признака: чем слабее вариация, тем круче кривая распределения при данном масштабе. Чтобы показать, в чем состоит эксцесс распределения, и правильно его интерпретировать, нужно сравнить ряды с одинаковой силой вариации (одной и той же величиной σ) и разными показателями эксцесса. Чтобы не смешать эксцесс с асимметрией, все сравниваемые ряды должны быть симметричными. Поскольку эксцесс норм распред равен 3, пок-ль эксцесса вычисляется по ф-ле 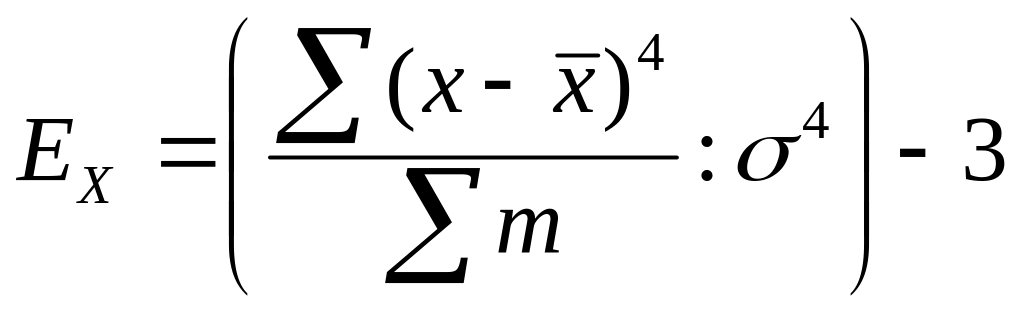или где нормированный момент 4 порядка. При Е_Х>0 высоковершинный эксцесс распред. При Е_Х<0 низковершинный. При Е_Х=0 норм распред. Для оценки существенности эксцесса вычисляют пок-ль его ср квадратич ошибки Если отношение имеет значение больше 3, то это свидетельствует о существенном характере эксцесса.