Поле комплексных чисел.

Задача. Вычислите .

Решение:

Вычисление проведем по действиям:

1) .

2) .

3) .

Задача. Найдите для следующего комплексного числа его тригонометрическую форму а) , б) .

Решение:

а) .

. Зная длину радиус- вектора - и его направление – угол отклонения радиус-вектора от положительного направления оси против часовой стрелки , запишем тригонометрическую форму данного комплексного числа: .

б) .

Задача. Вычислите , используя формулу Муавра.

Решение:

1 шаг. Запишем число в тригонометрической форме .

2 шаг. Применим формулу Муавра:

Задача. Решите уравнение в поле комплексных чисел .

Решение:

. Найдем все корни -ой степени из 16, используя теорему о том, что каждый корень -ой степени из ненулевого комплексного числа есть произведение некоторого известного корня и корня -ой степени из 1.

1 шаг. Выпишем все корни 4-ой степени из 1:

2 шаг. Применим указанную теорему, зная, что 2 – один из корней 4-ой степени из 16:

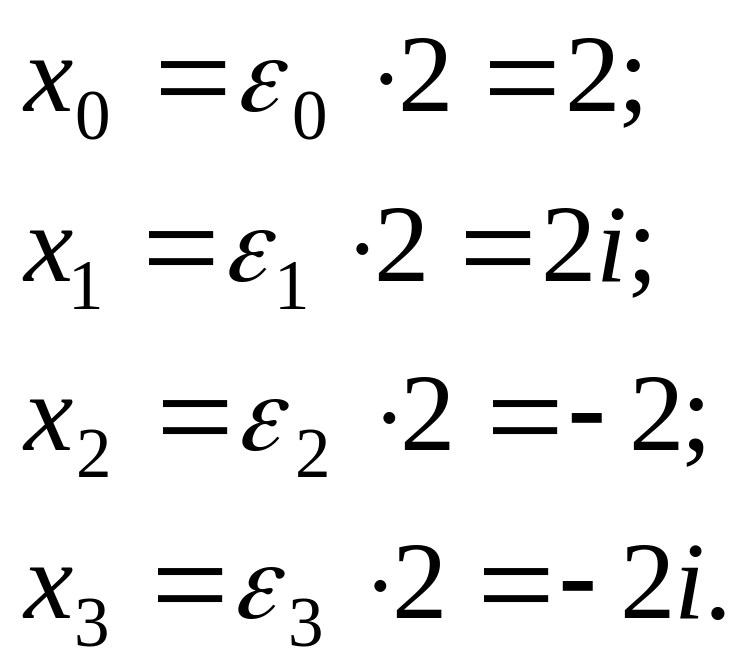
Задача. Решите уравнение .

Решение:

Пусть . Тогда . Подставим в уравнение:

Последнее эквивалентно системе: .

; ; ; ; ; .

Таким образом, .

Гомоморфизмы алгебр. Подалгебры. Расширения алгебр. Упорядоченные алгебры.

Задача. Опишите все автоморфизмы аддитивной полугруппы натуральных чисел.

Решение:

Рассмотрим произвольный автоморфизм . Поскольку полугруппа циклическая и порождается , то для задания автоморфизма достаточно указать образ порождающего элемента. Предположим . Тогда

.

Таким образом, любой автоморфизм аддитивной полугруппы натуральных чисел имеет вид для некоторого .

Задача. Докажите, что поле наименьшее подполе поля , содержащее .

Решение:

Докажем методом от противного. Предположим, существует некоторое поле такое, что и . Известно . Поскольку - наименьшее из всех числовых полей, то . Таким образом, произвольный элемент поля также является элементом поля , так как . Последнее означает , что противоречит предположению, следовательно, - наименьшее из числовых полей, содержащее .

Задача. Выясните, является ли кольцо , где , упорядоченным.

Решение:

Предположим, что в существует положительный конус . Очевидно, . Тогда, по второй аксиоме положительного конуса, . Последнее противоречит первой аксиоме положительного конуса, следовательно, нельзя упорядочить.

Задача. Докажите, что в упорядоченном кольце квадрат любого не равного нулю элемента положителен.

Решение:

Докажем методом от противного. Предположим, в упорядоченном кольце с положительным конусом существует элемент такой, что . Возможны случаи:

1. .

1.1. . Тогда . Получили противоречие с условием .

1.2. . Тогда . Получили противоречие с условием .

2. .

2.1. . Тогда . Получили противоречие с первой аксиомой положительного конуса .

2.2. . Тогда . Получили противоречие с первой аксиомой положительного конуса.

Таким образом, предположение неверно, и .