Указания к решению задач Аксиоматическая теория натуральных чисел.
Задача.
Выяснить,
какие из аксиом Пеано выполняются на
множестве А
с заданной на нем операцией f,
где
.
Решение:
Элементы 3, 6, 12,… не имеют предшествующих, т.к. нет таких натуральных чисел, которые бы в квадрате были равны 3, 6, 12,… . Однако, никакое из чисел не удовлетворяет первой аксиоме Пеано, в силу отсутствия единственности существования такого элемента. Таким образом, первая аксиома Пеано не выполняется.
Докажем, что вторая выполняется, предварительно записав ее в следующем виде:
.
.
Перепишем третью аксиому Пеано в следующем виде:
(*),
где
– выделенный элемент множества А,
удовлетворяющий первой аксиоме Пеано.
Поскольку элемента
не существует во множестве А, то
заведомо ложный конъюнктивный член,
значит, посылка импликации ложна, но
тогда импликация (*) истинна. Таким образ,
третья аксиома Пеано выполняется.
Задача.
Докажите
.
Решение:
1. База индукции n = 1.
.
2. Пусть верно для n = k.
.
3. Проверим для n = k+1.
.
Задача.
Докажите, что для любого натурального
n
делится на 3.
Решение:
1. База индукции n = 1.
.
2. Пусть верно для n = k.
.
3. Проверим для n = k+1.
Задача.
Докажите
неравенство 
для любого натурального 
.
Решение:
1. База индукции n = 5.
2. Пусть верно для n = k.
3. Проверим для n = k+1.
Кольцо целых чисел. Упорядоченность кольца целых чисел.
Задача.
Докажите
равенство следующих целых чисел: 
.
Решение:
Целые
числа являются классами эквивалентности
фактормножества
по отношению ~, заданному следующим
образом:
.
Классы эквивалентности равны тогда и только тогда, когда их порождающие элементы лежат в отношении ~. Воспользуемся последним утверждением для доказательства равенства :
.
Задача.
Вычислите: 
.
Решение:
Поскольку
натуральное число n
отождествляется с классом эквивалентности
вида 
,
имеем:
.
Зная,
что
,
получим
.
Вычислим по действиям:
.
Действительно,
.
Тогда 
.
Задача.
Проверьте,
выполняется ли следующее неравенство
.
Решение:
.
Рассмотрим
разность целых чисел 
и 
Поскольку полученное число не лежит в положительном конусе N множества Z, неравенство ложное.
Действительно,
Тогда
ложное неравенство.
Поля рациональных, действительных чисел и их упорядоченность.
Задача.
Докажите
равенство следующих рациональных чисел:
.
Решение:
Поскольку
,
то
.
Зная,
что 
,
получим
.
Рациональные
числа 
равны как классы эквивалентности тогда
и только тогда, когда их порождающие
элементы лежат в отношении 
,
т.е. ad=bc.
.
Задача.
Вычислите
.
Решение:
.
Зная,
что рациональное число 
отождествляется с целым числом
,
получим 
.
.
Действительно,
.
Задача.
Проверьте,
выполняется ли следующее неравенство
.
Решение:
.
Рассмотрим
разность рациональных чисел
и
.
.
Поскольку полученное число лежит в
положительной области
множества
,
неравенство верное.
Действительно,
.
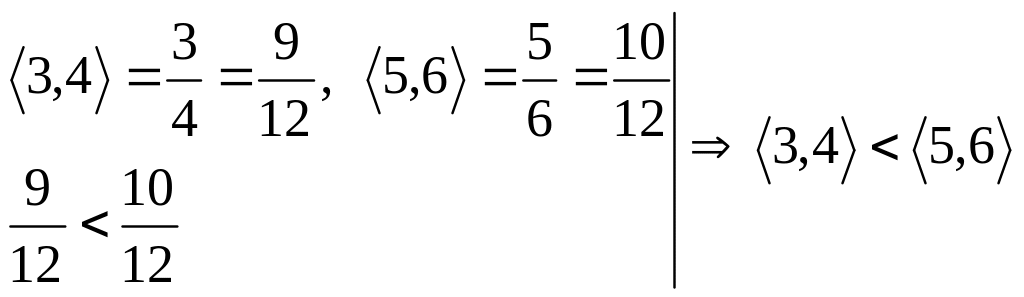Задача.
Придумайте
последовательность рациональных чисел,
сходящуюся к числу а)
;
б)
.
Решение:
а)
Рассмотрим последовательность
.
,
так как
.
а)
Рассмотрим последовательность
.
.
Задача.
Выясните,
какие из следующих последовательностей
рациональных чисел фундаментальны:
а)
;
б)
.
Решение:
а)
.
Таким образом, последовательность
сходится, а, значит, является фундаментальной.
б)
Последовательность
не является фундаментальной, поскольку
на бесконечности члены этой
последовательности с четными номерами
стремятся к
,
а с нечетными к
,
а, значит, расстояние между ними будет
неограниченно расти.
Задача.
Проверьте,
равны ли следующие действительные
числа:
Решение:
Действительные
числа
и
равны как классы эквивалентности тогда
и только тогда, когда их порождающие
элементы лежат в отношении ,
т.е. последовательность
- нулевая. Последнее условие равносильно
следующему:
.
действительные
числа
и
не равны.
Задача.
Вычислите
.
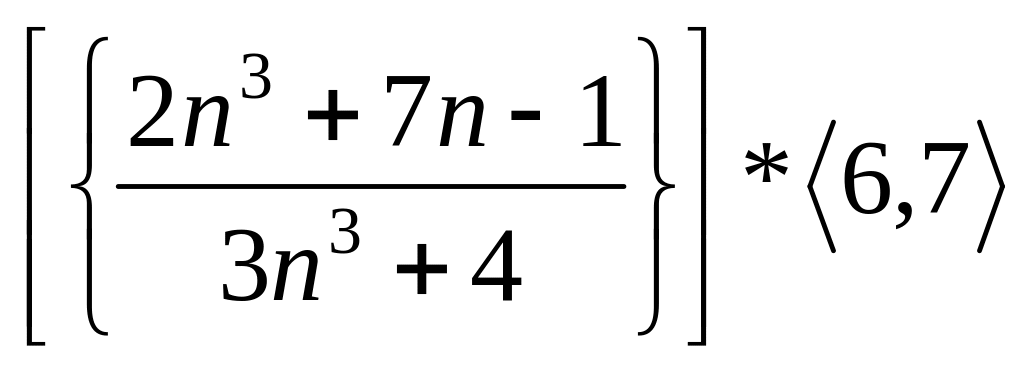Решение:
Поскольку
рациональное число
также является действительным,
следовательно, совпадает с классом
эквивалентности фундаментальных
последовательностей рациональных
чисел, сходящихся к
.
Тогда
.
Таким образом,
.
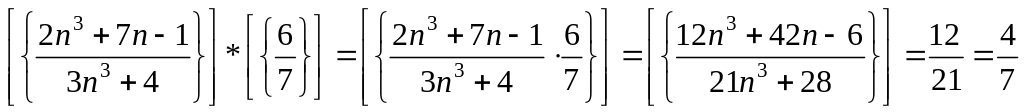Задача.
Проверьте,
выполняется ли следующее неравенство
.
Решение:
-
положительная последовательность.
Рассмотрим
разность действительных чисел
и
.
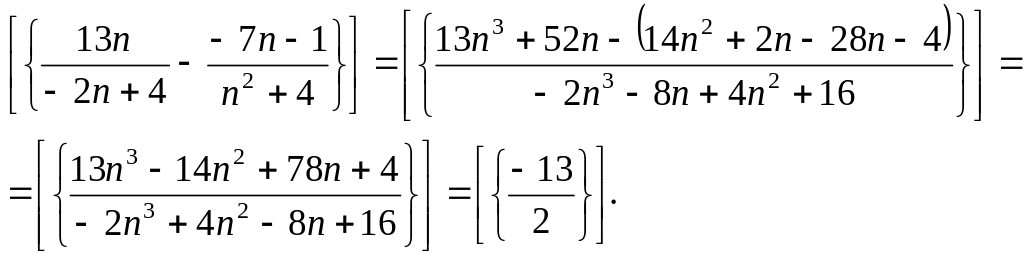
Таким образом, неравенство неверно, так как разность есть класс эквивалентности, порожденный отрицательной последовательностью.
Действительно,
,
но
неравенство ложное.