билеты 1 сем / 61-66

Высшая математика. Билеты 61 – 66

61. Критерий постоянства функции. Пример

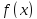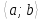Пусть функция определена и дифференцируема на промежутке . Эта функция постоянна на данном промежутке тогда и только тогда, когда её производная на этом же промежутке тождественно равна 0:

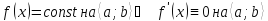
Доказательство: а) необходимость: это очевидно, так как ;

б) достаточность: Пусть зафиксировано и По формуле Лагранжа , где с лежит между .

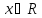
Пример: при на R. Следовательно, 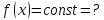Пусть . Поэтому 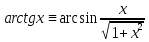на R.

62.Критерий монотонности функции. Пример

Пусть функция 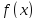определена и дифференцируема на промежутке . Эта функция монотонно возрастает (убывает) на данном промежутке тогда и только тогда, когда её производная на этом же промежутке неотрицательна (неположительна):

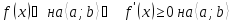и

Доказательство: а)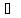 необходимость: Рассмотрим случай, когда функция возрастает (для убывающей функции всё аналогично). Пусть , тогда 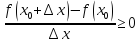. Следовательно,

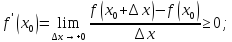
б)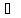 достаточность: Пусть 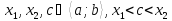; по формуле Лагранжа, отсюда

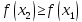
Пример: 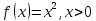. . 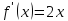При x>0 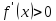, значит, здесь функция монотонно возрастает (и действительно, мы рассматривали правую ветку обычной параболы, монотонно возрастающую).

63. Необходимый признак точки экстремума

Если функция дифференцируема в точке с и имеет в этой точке локальный экстремум, то

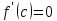
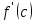Доказательство: В точке локального экстремума с функция не может ни возрастать, ни убывать. Соответственно, и производная не может быть ни положительной, ни отрицательной, то есть .

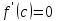Геометрический смысл: Если в точке кривой , соответствующей локальному экстремуму функции 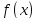, существует касательная к графику , то эта касательная параллельна оси .

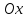Замечание 1: Это недостаточный признак точки экстремума.

Замечание 2: Функция может иметь экстремум в точке, где её производная не существует.

64. Первый достаточный признак точки экстремума. Примеры

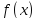Утверждение: Пусть точка с – точка, подозрительная на экстремум (точка возможного экстремума: ), а функция дифференцируема в . Тогда, если в пределах этой окрестности производная меняет знак, то точка с – точка локального экстремума; если знак не меняется, то экстремума в этой окрестности нет. То есть если при

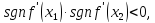то экстремум есть, а если то нет.

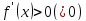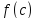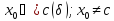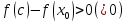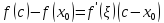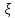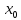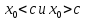
Доказательство: Пусть в данной окрестности слева от с и справа от с (Нужно доказать, что – максимальное (минимальное) значение в этой окрестности). Пусть . Доказать, что . По теореме Лагранжа , где лежит между и . При , при , следовательно, . Аналогично доказывается, что если с обеих сторон от с, то при 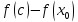имеет разные знаки, то есть в этом случае экстремума нет.

Замечание: Порой не получается определить знак производной (смотри пример 2)

Примеры: 1) 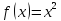, , 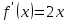x=0 – точка, подозрительная на экстремум.

При при 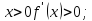производная меняет знак, значит, х=0 – точка экстремума (вернее, минимума – вершина обычной параболы).

2) : Здесь вроде 0 – подозрительная точка, но доказать экстремум так не получится. На самом же деле в точке 0 существует бесконечное множество точек экстремума.

65.Второй достаточный признак точки экстремума. Примеры

Можно использовать, если сложно определить знак производной слева и справа от точки возможного экстремума с, но легче посчитать вторую производную.

Утверждение: Пусть 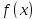имеет в точке с конечную вторую производную. Тогда 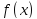имеет в точке максимум, если , и минимум, если .

Доказательство: Разложим 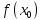в ряд Тейлора с остаточным членом Пеано (первый член - нулевую производную – переносим сразу влево):

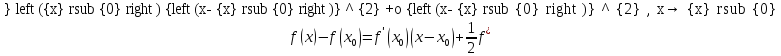
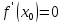Здесь левая часть равна , так как , а в правой части (см. билет 64)

Тогда 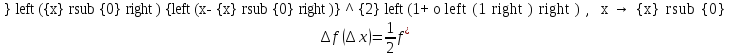. Видно, что приращение функции зависит только от знака 2-й производной, так как остальные множители неотрицательны.

Замечание: Данная теорема применима не всегда и имеет более узкую сферу действия, чем 1-ая. Она не работает, если 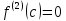или не существует.

Примеры: 1) 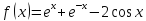, нули функции:

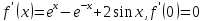– точка, подозрительная на экстремум.

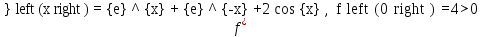, тогда 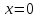– точка минимума.

66. Нахождение наибольших и наименьших значений функции. Пример

Утверждение: Пусть 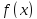определена, непрерывна и имеет n производных на 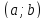. Пусть существует – точка, подозрительная на экстремум и , где 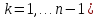причём 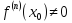. Если n=2m (чётное), то в точке находится либо максимум, либо минимум. Если же n=2m-1 (нечётное), то экстремума нет.

Доказательство: 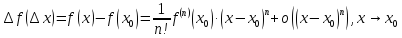(ряд Тейлора – Пеано).

При n=2m

При n=2m-1

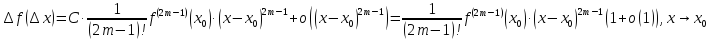
Примеры: 1) 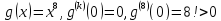, значит, в нуле есть экстремум (если точнее – минимум, ведь это обычная парабола)

2) 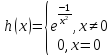Здесь данная теорема не работает, но в нуле будет минимум.

Далее нужно найти точки максимума и минимума, используя материал билетов 63-65. Впоследствии находится значение максимума (минимума) с помощью подстановки значения 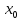в исходную функцию .

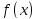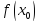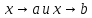Замечание: Найденные максимумы (минимумы) – локальные, то есть на рассматриваемом промежутке могут быть значения, большие (меньшие) . Поэтому всегда следует проверять граничные точки (или пределы функции при , если a и b не входят в промежуток)