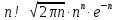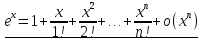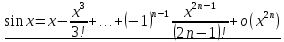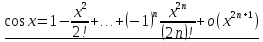билеты 1 сем / 55-60
.docxВысшая математика. 1 семестр. Билеты 55 - 60
55. Теорема Тейлора – Пеано
Применяется для приблизительного вычисления функции, когда достаточно узнать не величину погрешности, а только её порядок малости.
Пусть
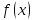 имеет производные до n-го
порядка включительно в
имеет производные до n-го
порядка включительно в
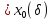 .
Тогда формулу Тейлора можно представить
в виде:
.
Тогда формулу Тейлора можно представить
в виде:
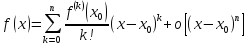 при
при
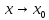 ,
или:
,
или:
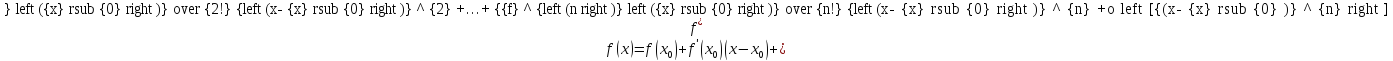 ,
где бесконечно малую функцию
,
где бесконечно малую функцию
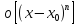 называют остаточным членом
в
форме Пеано.
называют остаточным членом
в
форме Пеано.
56. Свойства функций, дифференцируемых в точке до n-го порядка включительно
Производная
высшего порядка
(порядка n):
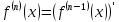 ,
где
,
где
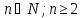 ;
;
(Дифференциал
высшего порядка:
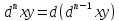 );
);
Формула
Лейбница:
Если функции
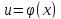 и
и
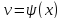 n
раз дифференцируемы, то
n
раз дифференцируемы, то
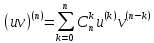
(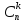 – число сочетаний из n
элементов по k,
– число сочетаний из n
элементов по k,
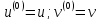 )
)
n-ные производные элементарных функций:
1)
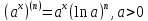 1.1)
1.1)
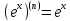
2)
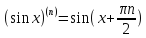
3)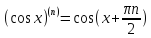
4)
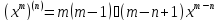
5)
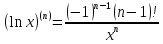
57. Вывод формул Тейлора для основных элементарных функций
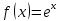 :
:
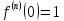 ;
;
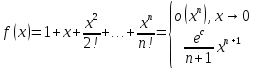
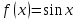 :
:
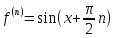 ;
;
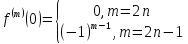
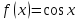 :
:
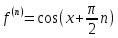 ;
;
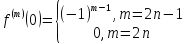
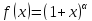 :
:
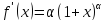 ;
;
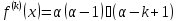 ;
;
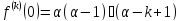
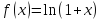 :
:
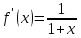 ;
;
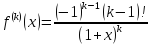 ;
;
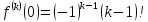
58. Вычисление неопределённостей методом выделения главных частей. Пример
В
многочлене Тейлора
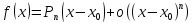
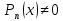 называют главной
частью
функции
называют главной
частью
функции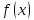 в окрестности точки
в окрестности точки
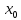 .
Тогда, при вычислении предела главная
часть функции будет эквивалентна всей
функции:
.
Тогда, при вычислении предела главная
часть функции будет эквивалентна всей
функции:
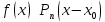 при
при
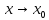 .
.
Пример:
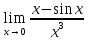 1) Разложим по Тейлору
1) Разложим по Тейлору
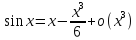 ;
;
2)
к обеим частям можно добавить –х: при
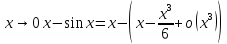 , или
, или
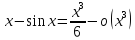 ,
что эквивалентно выражению
,
что эквивалентно выражению
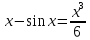 ;
;
3)
подставляем:
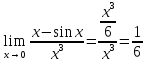
59. Три теоремы Лопиталя. Замечания и примеры
Правило
Лопиталя:
Если предел отношения 2-х функций
представляет собой неопределённость
вида
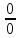 или
или
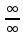 ,
то предел отношения этих функций равен
пределу отношения их производных.
,
то предел отношения этих функций равен
пределу отношения их производных.
Теоремы Лопиталя
Теорема
1:
Пусть
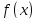 и
и
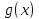 определены на
определены на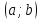 ;
;
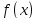 и
и
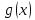 имеют производные на
имеют производные на
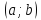 ;
;
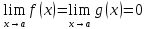 ;
Пусть
;
Пусть
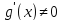 на
на
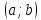 ;
существует
;
существует
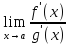 ;
Тогда выполняется равенство:
;
Тогда выполняется равенство:
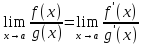
Доказательство:
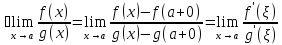 по теореме Коши, где
по теореме Коши, где
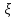 – немая переменная
– немая переменная
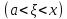 ;
;
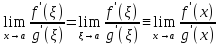
Пример:
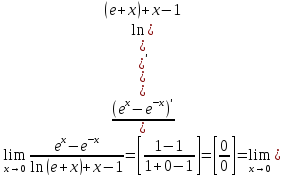 Получается такой же ответ, как при
решении через ряд Тейлора.
Получается такой же ответ, как при
решении через ряд Тейлора.
Теорема
2:
Пусть
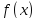 и
и
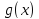 определены на
определены на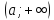 ;
;
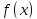 и
и
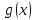 имеют производные на
имеют производные на
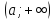 ;
;
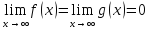 ;
Пусть
;
Пусть
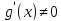 на
на
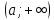 ;
существует
;
существует
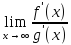 ;
Тогда выполняется равенство:
;
Тогда выполняется равенство:
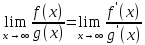
Доказательство:
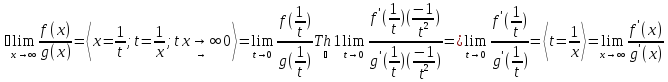
Пример:
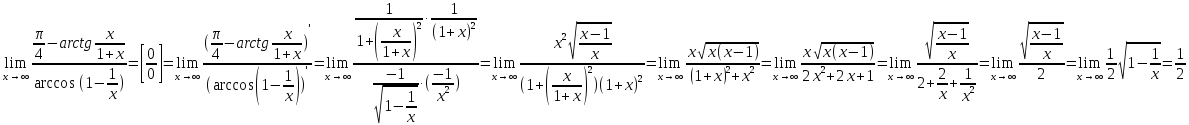
Теорема
3:
Пусть
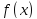 и
и
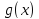 определены на
определены на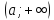 ;
;
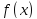 и
и
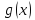 имеют производные на
имеют производные на
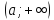 ;
;
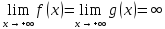 ;
пусть
;
пусть
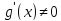 на
на
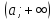 ;
существует
;
существует
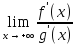 ;
тогда выполняется равенство:
;
тогда выполняется равенство:
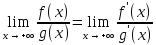
Доказательство: Смотри доказательство теоремы 2.
Пример:
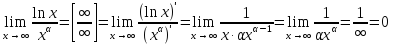
Примечание:
Правило Лопиталя можно применять к
пределу несколько
раз
и комбинировать с другими преобразованиями
при необходимости (если даже после
других преобразований остаётся
неопределённость
вида
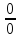 или
или
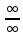 ).
).
60.
Теорема Штольца. Вычисление
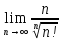 .
Формула Стирлинга
.
Формула Стирлинга
Теорема
Штольца:
Пусть
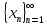 и
и
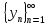 - бесконечно большие последовательности.
Если существует предел
- бесконечно большие последовательности.
Если существует предел
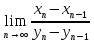 ,
то существует предел отношения
,
то существует предел отношения
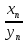 ,
равный ему:
,
равный ему:
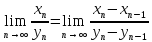
Замечание:
Если
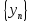 – бесконечно большая возрастающая
последовательность, а последовательность
– бесконечно большая возрастающая
последовательность, а последовательность
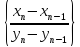 тоже бесконечно большая и стремится к
бесконечности определённого знака, то
последовательность
тоже бесконечно большая и стремится к
бесконечности определённого знака, то
последовательность
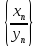 бесконечно большая.
бесконечно большая.
Пример:
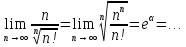
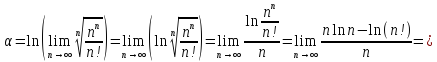 по
Th. Штольца
по
Th. Штольца
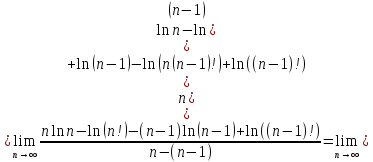 , тогда
, тогда
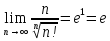
Формула Стирлинга:
При
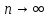 факториал n
можно заменить на эквивалентную функцию:
факториал n
можно заменить на эквивалентную функцию: