билеты 1 сем / 37-54

Мат. анализ. Вопросы 37-54

37. Теорема о достаточных условиях непрерывности функции на промежутке

Соответственно, для промежутка: все точки промежутка удовлетворяют данному равенству.

38. Теорема о монотонности и непрерывности обратной функции Th. О обратной функции

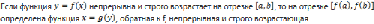
Доказательство: 1) Монотонность: 2) Непрерывность: 39. Теорема о непрерывности основных элементарных и элементарных функций. Примеры

Th. О непрерывности элементарных функций Все основные элементарные функции непрерывны при всех значениях x, для которых они определены. Доказательство: Элементарная функция – формула, задаваемая конечным числом арифмитических действий и суперпозиций (операция взятия функции от функции) основных элементарных функций. Из основных теорем о непрерывности вытекает доказательство.

Примеры: 40. Определение производной функции в точке. Необходимое условие существования производной. Вычисление производных основных элементарных функций Необходимое условие существования производной:

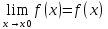
Вычисление производных основных элементарных функций:

41. Теоремы о производной суммы, произведения и частного.

42. Теорема о производной сложной функции. Примеры Примеры: 43. Теорема о производной обратной функции. Примеры Примеры:

44. Определение касательной к графику функции и теорема о достаточных условиях существования касательной к графику

45. Бесконечные и односторонние проивзодные. Примеры Примеры: 46. Критерий дифференцируемости функций в точке. Следствие Критерий дифференцируемости функции: Для того чтобы функция f являлась дифференцируемой в данной точке x₀, необходимо и достаточно, чтобы она имела в этой точке конечную производную. Следствие:

47. Определение, свойства и геометрический смысл дифференциала функции

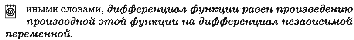
Геометрический смысл: 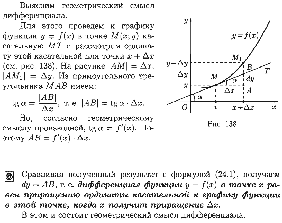Основные теоремы и свойства:

48. Свойства производной и дифференциала n-го порядка. Формула Лейбница Свойства производной и дифференциала n-го порядка:

Формула Лейбница для произведения:

Доказательство методом МИ:

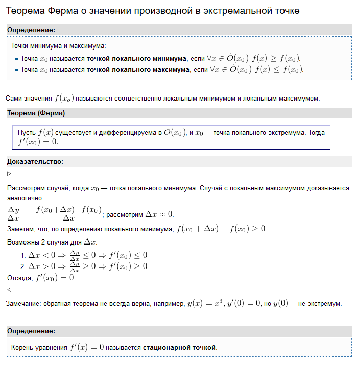
49. Теорема Ферма

50. Теорема Дарбу51. Теорема Ролля

Следствия (будет применяться Теорема Лагранжа, вопрос 53):

52. Теорема Коши, ее геометрический смысл Следствия: Геометрический смысл: 53. Теорема Лагранжа, ее геометрический смысл Геометрический смысл:

54. Теорема Тейлора-Лагранжа. Следствия