4. Производные
8. Дифференциальные уравнения
Дифференциальные уравнения имеют вид:
Порядок дифференциального уравнения зависит от наивысшего порядка производной, входящей в это уравнение:
Дифференциальные уравнения любого прядка можно решать последовательным интегрированием только если слева от знака “=” стоит производная любого порядка, а справа от знака “=” стоит функция только от x:
Например:
Общим решением дифференциальных уравнений является:
В общем решении должны присутствовать произвольные постоянные. Их столько, каков порядок дифференциального уравнения.
Частное решение получается из общего при определённых значениях произвольных постоянных. Чтобы найти частное решение, обязательно должны быть начальные условия.
Геометрически общее решение дифференциального уравнения — семейство интегральных кривых. Чтобы найти частное решение, надо найти определённые произвольные постоянные. Частное решение — единственная интегральная кривая, проходящая через точку, соответствующей начальным условиям.
Дифференциальные уравнения первого порядка
Дифференциальные уравнения с разделёнными переменными:
Простейшие дифференциальные уравнения с разделяющимися переменными:
Общий вид:
(разделим на
,
т. е. делим на то, что мешает проинтегрировать
уравнение)
и далее проинтегрируем, как с разделёнными
переменными.
Например:
(т. к. сумма логарифмов есть логарифм
произведения)
Линейные дифференциальные уравнения
Общий вид:
.
Решаются такие уравнения:
,
Из этого уравнения выражаем V, подставляем в предыдущее уравнение, находим U.
Ответ записываем так: . Например:
Однородные дифференциальные уравнения
Общий вид:
,
где
и
— однородные функции
— однородная, если
.
Решаются такие уравнения заменой
.
Например:
(умножим на
)
(разделим на
)
.
После интегрирования получим:
Ответ:
.
Дифференциальные уравнения второго порядка
Уравнение, содержащее производные или дифференциалы второго порядка, называются дифференциальными уравнениями второго порядка:
Общим решением уравнения
называется функция
,
содержащая две произвольные постоянные
и
и удовлетворяющая условиям:
при любых значениях постоянных и функция является решением дифференциального уравнения;
каковы бы не были начальные условия
,
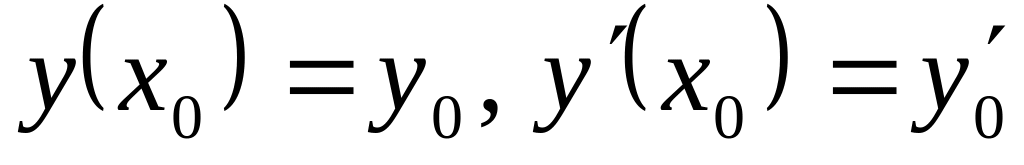существуют единственные значения
и
такие, что функция
является решением дифференциального
уравнения и удовлетворяет начальным
условиям.
Частным решением дифференциального
уравнения второго порядка уравнения
называется всякое решение
,
получающееся из общего решения
при фиксированных значениях
и
.
Простейшие уравнения второго порядка имеют вид:
или
.
Уравнение такого вида решается двукратным
интегрированием.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами (ЛОДУ)
ЛДУ второго порядка называются уравнения
вида
,
где
и
— постоянные величины, а
— непрерывная функция.
Уравнения вида называются ещё неоднородными дифференциальными уравнениями второго порядка.
Если
,
то уравнение
принимает вил:
— ЛОДУ второго порядка с постоянными
коэффициентами
и
.
Теорема 1
Если
— решение уравнения
,
то и
,
где
— постоянный множитель, также будет
решением данного уравнения.
Теорема 2
Если
,
— решение уравнения
,
то и сумма
также будет решением данного уравнения.
Два частных решения уравнения называются линейно зависимыми, если одно из них может быть получено умножением другого на какой-либо постоянный множитель, в противном случае частное решение называют линейно независимыми.
Теорема 3
Если
и
— линейно независимые частные решения
уравнения
,
то общее решение его будет
,
где
и
— произвольные постоянные величины.
Частными линейно-независимыми решениями
уравнения
являются функции вида:
,
где k — произвольное число, которое
нужно найти.
Решение ЛОДУ второго порядка с постоянными коэффициентами
Составим характеристическое уравнение
ЛОДУ второго порядка с постоянными
коэффициентами:
Решая это квадратное уравнение:
,
получим
Ответ в общем виде:
,
получим
Ответ в общем виде:
, получим комплексные корни:
Ответ в общем виде:
