3.5. Каналовые поверхности
Канловой поверхностью называется поверхность, образованная непрерывным каркасом замкнутых плоских сечений, определенным образом ориентированных в пространстве. Площади этих сечений могут оставаться постоянными I вши монотонно меняться в процессе перехода от одного сечения к другому.
В инженерной практике наибольшее распространение получили два способа ориентирования плоскостей образующих: параллельно какой-либо плоскости — каналовые поверхности с плоскостью параллелизма, перпендикулярно к направляющей линии - прямые каналовые поверхности. Каналовые поверхности применяются для конструирования переходных участков между двумя поверхностями типа трубопроводов.
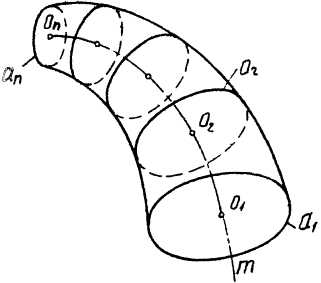
Частным случаем каналовой поверхности является циклическая поверхнось. Циклической поверхностью называется поверхность, которая образуется окружностью а постоянного или переменного радиуса, центр которой перем ещается по криволинейной направляющей т (рис. 3.40).
|
|
Для задания циклической поверхности необходимо задать закон изменения радиуса образующей окружности и закон движения образующей. Оба закона могут быть заданы как аналитически, так и графически. Выше были рассмотрены некоторые поверхности, которые можно отнести к циклическим. Это, во-первых, поверхности вращения и, во-вторых, те из поверх частей второго порядка, которые имеют круговые сечения. |
Рис. 3.40 |
||
Одним из частных видов циклических поверхностей являются трубчатые поверхности переменного радиуса.
Трубчатая поверхность образуется движением окружности а переменного радиуса, происходящим так, что центр О окружности перемещается по криволинейной направляющей, при этом плоскость окружности остается перпендикулярной к направляющей (рис. 3.40, а).
Последовательные положения образующей окружности а составляют каркас поверхности. Направляющей является осевая линия т. Если осевая линия - прямая, то получается поверхность вращения.
Для задания трубчатой поверхности переменного радиуса надо задать осевую линию т и закон изменения радиуса по длине дуги т: R—f(m) (рис. 3.40, б). Определитель такой поверхности: Ф [тЛ = f{m)), Если радиус образующей окружности остается постоянным, то поверхность называется просто трубчатой, ее определитель Ф (а,т). Если направляющей т будет винтовая линия, то получается трубчатая винтовая поверхность. Примером применения в технике такой поверхности является цилиндрическая пружина, образованная навертыванием стальной проволоки круглого сечения на цилиндрический стержень.
3.6. Поверхности параллельного переноса
Поверхностью параллельного переноса называется поверхность, образованная непрерывным поступательньш перемещением плоской линии а по направляющей кривой т, при этом образующие а остаются параллельными между собой.
|
|
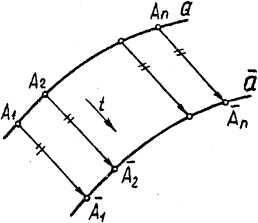
Под параллельными кривыми линиями подразумевают линии, полученные одна из другой путем параллельного переноса каждой из точек на одинаковое расстояние. Так на рис. 3.41 кривая а - параллельна кривой ау так как точки А,, А2... А„ кривой а получены из точек А|, Аз ...А„кривой а путем переноса их по параллельным прямым В (А А ... А„ А„) на величину вектора. Для образования сложной поверхности параллельный перенос кривой линии следует осуществлять с помощью мгновенных векторов переноса, характер изменения направления которых задается кривой т (направление векторов переноса определяется хордами кривой т). |
Рис. 3.41 |
Рис. 3.42 |
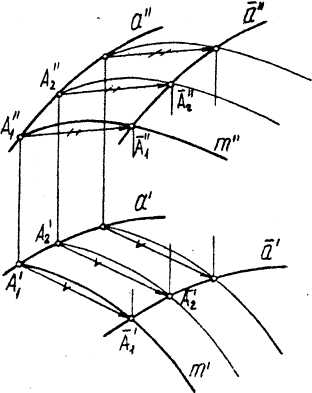
Определитель поверхности параллельного переноса имеет вид Ф (а,т)[Л].
На рис. 3.42 поверхность параллельного переноса задана на эпюре Монжа определителем. Для того, чтобы построить ее каркас достаточно: на кривой т(т\тп) наметить ряд точек А(А',А"), а(а'А")...; через эти точки провести кривые, параллельные кривой а. Проведение проекций параллельных кривых сводится к проведению параллельных линий. Это следует из свойства параллельного проецирования, состоящего в том, что проекции равных и параллельных отрезков равны и параллельны. На рис. 3.42 такими отрезками являются стороны параллелограмма A{ A, a\ a2 , аппроксимирующего участок криволинейной поверхности отсеком плоскости. Из чертежа видно, что образующую и направляющую можно поменять местами.