3.3. Линейчатые поверхности

Определение. Линейчатой поверхностью называется поверхность, кото­рая может быть образована движением прямой линии в пространстве.

В зависимости от закона перемещения образующей получаются различные типы линейчатых поверхностей.

3.3.1. Линейчатые поверхности с одной направляющей (торсы) А. Коническая и пирамидальная поверхности

Коническая поверхность образуется прямой линией а (образующей), которая скользит по кривой линии т (направляющей), имея при этом неподвижную точку S (вершину).

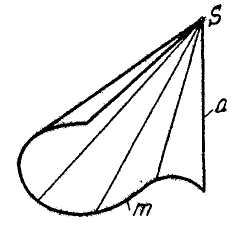
Определитель конической поверхности состоит из вершины S и направляю­щей кривой т. т. е. Ф (т, S)\A] (рис. 3.20, а).

а б

Рис. 3.20

Задание на чертеже с помощью определителя приведено на рис. 3.20, б. Каркас поверхности может быть составлен из набора прямолинейных образую­щих. Точку N на поверхности строят при помощи образующей а, проходящей че­рез вершину S и точку 1, принадлежащую направляющей т.

Если направляющей поверхности служит ломаная линия, состоящая из пря­молинейных звеньев, то коническая поверхность превратится в пирамидальную поверхность.

Б. Цилиндрическая поверхность и призматическая

Цилиндрическая поверхность образуется прямой линией а , которая скользит по кривой линии т (направляющей), оставаясь параллельной самой себе

5>(рис. 3.2U

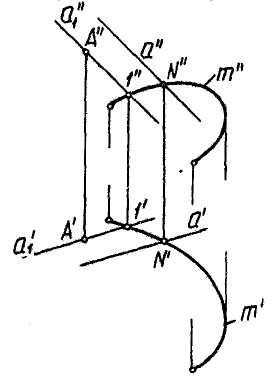
Цилиндрическую поверхность можно рассматривать как частный слу­чай конической поверхности, верщина которой удалена в бесконечность, и, следовательно, образующие параллель­ны друг другу (пересекаются в беско­нечно удаленной точке).

Определитель цилиндрической поверхности состоит из направляющей кривой т и образующей а: Ф (а, т)[А\. На рис. 3.21 приведено задание на чер­теже элементами определителя. Точка A{A'^i") построена на поверхности Ф при помощи образующей a_t, инцидент­ной поверхности, так как она проходит через точку 1, принадлежащую направ­ляющей т и параллельна заданной об­разующей а. Рис. 3.21

Если направляющей поверхности служит ломаная линия, то цилиндриче­ская поверхность превращается в призматическую.

Если направляющей цилиндрической и конической поверхности является кривая 2-го порядка, т. е. эллипс (окружность), гипербола, парабола, то образуется коническая или цилиндрическая поверхность 2-го порядка. Подробнее на них ос­тановимся при рассмотрении поверхностей вращения.

В. Поверхность с ребром возврата (торс)

Поверхностью сребром возврата (торсом), называется поверхность, об­разованная перемещением прямолинейной образующей а, касающейся во всех сво­их положениях некоторой пространственной кривой т, называемой ребром воз­врата.

Поверхности Способы образования поверхностей на чертеже

Будем рассматривать поверхность как совокупность всех последовательных положений движущейся линии.

Линия, которая при своем движении образует поверхность, называется образующей. Например, прямая а, перемещаясь образует цилиндрическую поверхность.

Образующая – необязательно должна быть прямой. Любая линия (в частности из тех, что мы рассматривали с вами) может при своем движении образовать поверхность. Кроме того, образующая в процессе перемещения может менять свою форму.

В зависимости от формы образующей могут быть получены различные поверхности. Однако форма поверхности будет зависеть не только от формы образующей, но и от закона перемещения образующей. Так, например, прямая, вращаясь вокруг паралельной ей прямой (оси) – образует цилиндрическую поверхность. Если прямая пересекается с осью она образует вращаясь вокруг нее коническую поверхность. Если прямая скрещивается с осью - однополостный гиперболоид.

Таким образом, все многообразующие поверхности может быть получено или изменением формы образующей или изменением закона ее перемещения, или и тем и другим одновременно.

Когда задают закон перемещения образующей, то большую роль играет направляющая линия – это линия, на которой скользит образующая при своем движении.

Любая линия на поверхности, которая пересекает все образующие может быть принята за направляющую.

Таким образом, на любой поверхности можно выделить два семейства кривых линий: семейство образующих и семейство направляющих, каждое из которых показывает всю поверхность и состоит из каких либо линий (плоских или пространственных).

Из линий, принадлежащих двум указанным семействам, может быть составлен каркас поверхности.

Учитывая непрерывность перемещения образующей, а следовательно непрерывность самой поверхности делаем важный вывод для теории поверхностей:

Через любую точку поверхности можно провести пару кривых, принадлежащих двум различным семействам линий на поверхности.

Рассматривая основные геометрические образы, изучением которых занимается начертательная геометрия, мы всегда исходим из кинематического способа образования данного геометрического образа.

Линия – совокупность всех положений движущейся точки, поверхность – совокупность положений движущейся линии.

Таким образом, чтобы определить, задать какой либо геометрический образ необходимо задать форму движущегося элемента (точка, линия) в каждый момент движению и закон этого движения.

Определителем геометрического образа будем называть фигуру постоянных независимых геометрических элементов, плюс алгоритм построения текущих точек или линий поверхности.

Определитель прямой линии – 2 точки. Если они заданы, то можно построить сколько угодно точек этой линии.

Определитель плоскости – 3 точки. Зная их, можно построить сколько угодно линий (прямых) этой плоскости.

Определитель рассмотренных выше цилиндрической поверхности – образующая а и направляющая.

Критерий задания поверхности: поверхность задана, если относительно любой точки пространства можно ответить на вопрос принадлежит она поверхности или нет (или можно построить любое число точек, линий, принадлежащих пов-ти).

Построение точки принадлежащей пов-ти производим по правилу: Точка принадлежит поверхности, если она принадлежит любой линии этой поверхности.